在树中,我们常常需要求两点间距离,而求两点的距离必然会经历两点共有的祖先节点,显然,祖先节点越近距离越近,因此我们引入最近公共祖先这个概念,并探究LCA这一求最近公共祖先的算法。
LCA算法分为离线算法和在线算法
离线算法( off line algorithms),是指基于在执行算法前输入数据已知的基本假设,也就是说,对于一个离线算法,在开始时就需要知道问题的所有输入数据,而且在解决一个问题后就要立即输出结果。
在线算法是指它可以以序列化的方式一个个的处理输入,也就是说在开始时并不需要已经知道所有的输入。
LCA的离线算法主要指的是基于深度优先搜索的tarjan算法。
对于一个图,我们从根节点开始进行深度优先搜索。
我们来想一下,假设询问的两个点 u , v 在不同的树枝,必然会有一个点 u 先被搜到(被搜到的意思是指访问已结束,所有相关的边已遍历过,所有的情况都已知),但是由于此时另一个点 v 还未被搜到,处于未知的状态,所以我们先回溯祖先节点 x,并
将 u 的祖先节点 x 记录下来,然后深搜会继续搜索 x 的另一根树枝,在搜索的过程当中如果正好搜索了另一个点 v 那么显然他们的最近公共祖先就是 x ,并且我们发现,x 在此前记录下 u 的祖先节点时已被记录,这样我们就找出了最近公共祖先,如果并没有
在其他数值搜到,那我们就继续回溯到祖先节点的祖先节点 y,并将 u 的祖先节点更新为 y ,然后再重复此过程,直到找出另一个点 v。
如果一个点 v 是另外一个点 u 的祖先,那么显然更加简单,我们只需不断更新 u 的祖先节点,直到祖先节点为 v ,因此和前面是一样的。
int vis[maxn];//标记已走过的节点 int f[maxn];//并查集记录节点当前的祖先节点 int ans[maxn];//记录每一组询问的结果 int Find(int x){ if(f[x]==x) return x; return f[x]=Find(f[x]);//路径压缩更新当前指向的祖先节点 } void tarjan(int u){ vis[u]=1,f[u]=u;//并查集初始化,标记该点为灰色(正在访问的状态) for(int i=head[0][u];i;i=e[0][i].next) { int v=e[0][i].to; if(vis[v]) continue; tarjan(v);//搜索子节点 f[v]=u;//子节点搜索结束后将子节点的父节点更新为当前节点 } vis[u]=-1; //所有边走完了标记为黑色(已经访问结束的状态) for(int i=head[1][u];i;i=e[1][i].next){//查找询问 int v=e[1][i].to; if(vis[v]==-1){//两点都访问结束后才进行查询,因为此时并查集才指向其祖先节点 ans[(i+1)/2]=Find(v);//当前节点的祖先节点就是最近公共祖先 } } }
搞清楚最主要的 tarjan 部分后我们只需要将整个图及所有询问全部都存好之后进行LCA算法就行。
这里为了方便查找与当前节点相关的询问,我们可以用一个边表来存储它。
类似的,我们可以利用这个算法求树上任意两点间的距离。
我们用一个数组 dis 来存储树上每个点到根结点的距离。
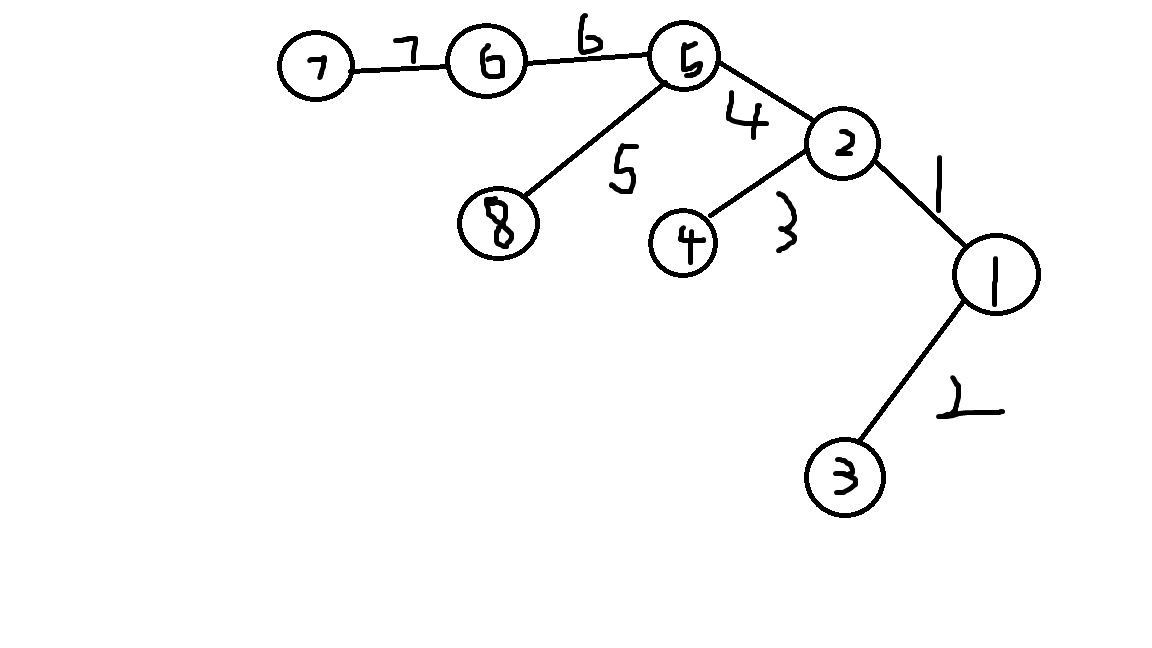
比如在这张图中,dis [ 7 ] = 18 , dis [ 8 ] = 10 ,dis [ 6 ] = 11 , dis [ 5 ] = 5。显然我们能得到:若 u 为 v 父节点,那么dis [ v ] = dis [ u ] + w,其中 w 为 u , v 间的边权。
假如我们要求 7 与 8 间的距离 。根据图我们能看出距离为 7 + 6 + 5 =18,我们要怎么利用 dis 求出来呢?
显然,dis [ 7 ] = 7 到 5 的距离 + 5 到 1 的距离, dis [ 8 ] = 8 到 5 的距离 + 5 到 1 的距离,也就是说 dis [ 7 ] +dis [ 8 ] = 要求的 7 到 8 的距离 + 2 * 5 到 1 的距离,而 5 正好是 7 和 8 的最近公共祖先,因此我们可以得出,若 u , v 的最近公共祖先为 x ,
那么 u 到 v 的距离就为 dis [ u ] + dis [ v ] - 2 * dis [ x ] 。
关于 dis 数组的维护,我们可以每次先根据 dis [ v ] = dis [ u ] + w 更新子节点的 dis 值然后再搜索该子节点。
上代码。
#include<cstdio> #include<iostream> using namespace std; const int maxn=1e4+5,maxm=4e4+5; struct Edge{ int to,w,next; }e[2][maxm]; int len[2],head[2][maxn]; void Insert(int u,int v,int w,int flag){ e[flag][++len[flag]].to=v; e[flag][len[flag]].w=w; e[flag][len[flag]].next=head[flag][u]; head[flag][u]=len[flag]; } int n,q; void Read(){ scanf("%d%d",&n,&q); for(int i=1;i<n;i++){ int u,v,w; scanf("%d%d%d",&u,&v,&w); Insert(u,v,w,0); Insert(v,u,w,0); } for(int i=1;i<=q;i++){ int u,v; scanf("%d%d",&u,&v); Insert(u,v,i,1); Insert (v,u,i,1); } } int vis[maxn]; int f[maxn],dis[maxn],ans[maxn]; int Find(int x){ if(f[x]==x) return x; return f[x]=Find(f[x]); } void tarjan(int u){ f[u]=u; vis[u]=1; for(int i=head[0][u];i;i=e[0][i].next){ int v=e[0][i].to; if(vis[v])continue; dis[v]=dis[u]+e[0][i].w; tarjan(v); f[v]=u; } vis[u]=-1; for(int i=head[1][u];i;i=e[1][i].next){ int v=e[1][i].to; if(vis[v]==-1){ ans[e[1][i].w]=dis[u]+dis[v]-2*dis[Find(v)]; } } } void sol(){ Read(); tarjan(1); for(int i=1;i<=q;i++){ printf("%d\n",ans[i]); } } int main(){ sol(); return 0; }


