ST表

　　对于一个乱序数组，我们常常会求某个区间内的最值，对此我们最常用的方法是直接 for 循环遍历找最值，但当询问增多时，显然这种方法时间效率过低，这时候我们就可以使用ST表来解决这个问题。

　　对于一个宽度为 2 ^j 的区间，我们可以将它分成长度都为 2 ^j-1 的两部分,显然，原区间的最值就等于这两个小区间最值中较大或较小者。ST表就基于这个思路上。

 

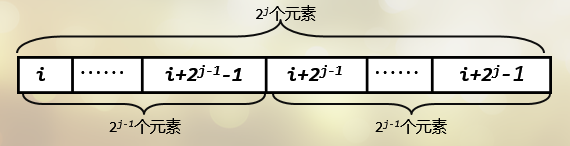
　　我们用一个 f [ i ] [ j ] 数组来记录从 i 开始 长度为 2 ^j 的区间中的最值，然后从小到大遍历区间宽度 2 ^j 中的 j 一直到2 ^j 大于数组长度，再遍历每一个起点（注意终点不能超出数组长度），那么根据上面的思路，我们可以将从 i 开始 长度为 2 ^j 的区间分为

两部分，也就是从i开始长度为 2 ^j-1 的区间以及从 i + 2 ^j-1 开始 长度为 2 ^j-1 的区间即 f [ i ][ j-1 ] 和 f [ i +(1 << (j-1)) ][  j-1 ]，因此我们得到：

　　f [ i ] [ j ] = max ( f [ i ] [ j-1 ] , f [ i + (1 << (j-1) )] [ j-1 ] ) ;

　　f [ i ] [ j ] = min ( f [ i ] [ j-1 ] , f [ i + (1 << (j-1) )] [ j-1 ] ) ;

　　同时 f 数组这个定义我们可以得到 f [ i ][ 0 ]是以 i 为起点宽度为1的区间，也就是数组中下标为 i 的本身。

　　由这两个性质我们就可以将整个ST表更新出来了。

　　

int n;
for(int i=1;i<=n;i++){
    scanf("%d",&a[i]);
    f[i][0]=a[i];
}
for(int j = 1;(1<<j) <= n;j++){//宽度 (从2开始)
    for(int i = 1;i + (1<<j) - 1 <= n;i++){//遍历起点（终点不能超出数组长度） 
        f[i][j]=max(f[i][j-1],f[i + (1<<(j-1))][j-1]);//从i开始的2的j次方可以分为两部分
        //从i开始宽度为2的j-1次方的区间 和 从（i+2的j-1次方）开始宽度为2的j-1次方的区间 
    }
}//预处理 

　　现在我们已经将整个ST表存储了起来，那么接下来只需处理询问就可以了。

　　但是我们又遇到了问题：询问的区间并不一定刚好是 2 的幂 ，也就是我们没办法直接从ST表中直接读取结果。

　　我们结合图来分析。

　　

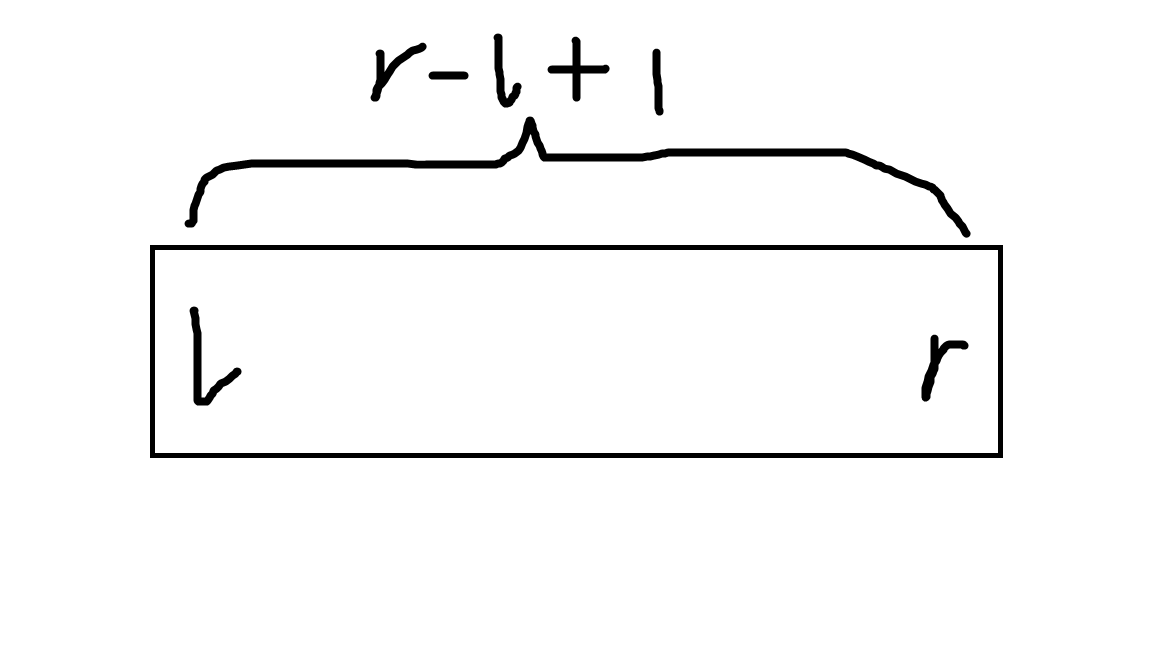
　　像这样一个以 l 为起点，r 为终点的区间，其长度显然为 r - l +1 。我们无法保证它刚好为 2 的幂，但是我们可以确定的是一定有不大于 r - l +1 的最大的 2的幂，有什么用呢？

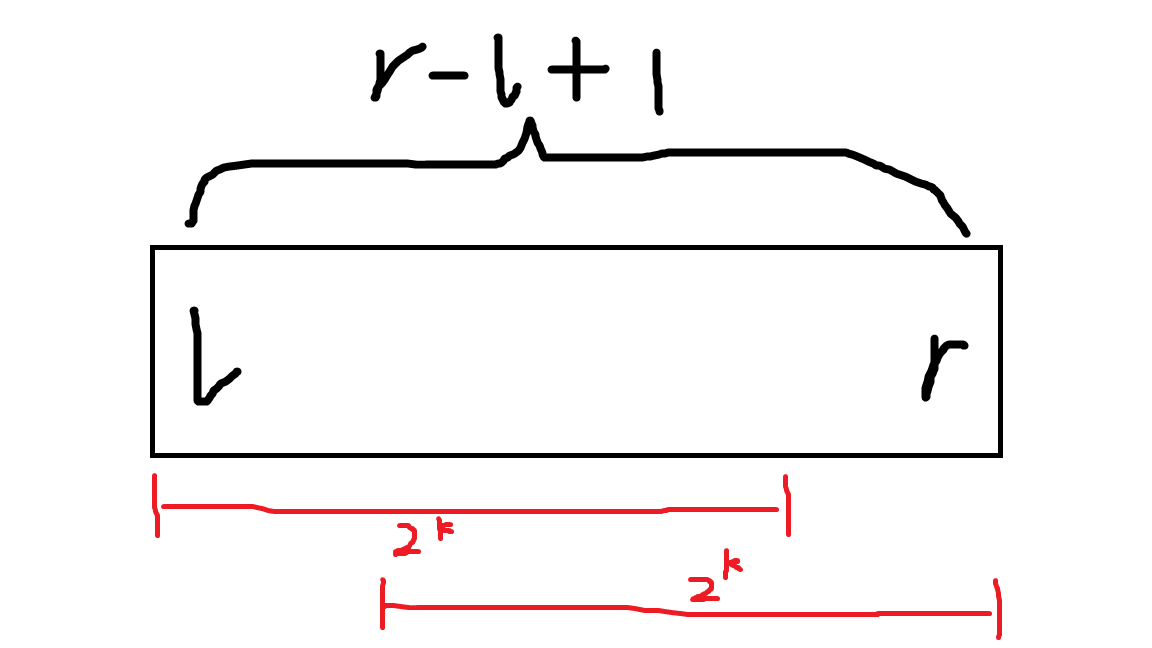
　　假定 2^k 为不大于 r - l +1 的最大的 2 的幂，那么当取如图所示的两个宽度同为 2^k 的区间刚好可以覆盖住整个要求的区间，因为要求的是最值，所以有重叠的部分其实并不会影响整个区间的最值，因此我们可以从这两个区间的最值中取出我们要的最值。

　　那为什么一定要取 2^k  为不大于 r - l +1 的最大的 2 的幂呢？我们将 2^k 再乘一个2，得到宽度为2 ^k+1 ，由于 2^k  为不大于 r - l +1 的最大的 2 的幂，所以 k 再 +1必然会超过 r - l +1，而 2 ^k+1 正好就为2 ^k + 2 ^k ，即两个宽度为 2 ^k 的区间挨着放，

这也就能保证两个2 ^k 区间一定能覆盖整个区间。

　　因此我们就能得到像这样一个以 l 为起点，r 为终点的区间，实际上可以分成两个宽度为2 ^k 的区间来求，而这两个区间因为必须刚好覆盖，所以必然有一个起点为 l ，一个终点为 r ，因此我们就能知道两个区间的起点与宽度，也就能在ST表中找到这两

个区间的最值。

　　ans = max( f [ l ] [ k ] , f [ r- ( 1 << k )  + 1 ] [ k ]);

　　ans = min( f [ l ] [ k ] , f [ r- ( 1 << k )  + 1 ] [ k ]);

　　这样我们就能解决这类问题了

#include<cstdio>
#include<iostream>
using namespace std;
const int maxn=1e5+5,maxm=2e6+5;
int a[maxn],f[maxn][20];//f[i][j]表示从i开始的宽度为2的j次方的区间最值 
int ans[maxm];
int Query(int l,int r){
    int k=0;
    while((1<<k) <= r-l+1) k++;
    k--;
    return max(f[l][k],f[r-(1<<k)+1][k]);
}
int n,m;
void Read(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        f[i][0]=a[i];
    }
    for(int j = 1;(1<<j) <= n;j++){//宽度 (从2开始)
        for(int i = 1;i + (1<<j) - 1 <= n;i++){//遍历起点（终点不能超出数组长度） 
            f[i][j]=max(f[i][j-1],f[i + (1<<(j-1))][j-1]);//从i开始的2的j次方可以分为两部分
            //从i开始宽度为2的j-1次方的区间 和 从（i+2的j-1次方）开始宽度为2的j-1次方的区间 
        }
    }//预处理 
    for(int i=1;i<=m;i++){
        int u,v;
        scanf("%d%d",&u,&v);
        ans[i]=Query(u,v);
    }
}
void sol(){
    Read();
    for(int i=1;i<=m;i++){
        printf("%d\n",ans[i]);
    }
}
int main(){
    sol();
    return 0;
}