Hot 100题刷题 Day 4

Day 4

相交链表

1. 题目：编写一个程序，找到两个单链表相交的起始节点。如下面的两个链表：

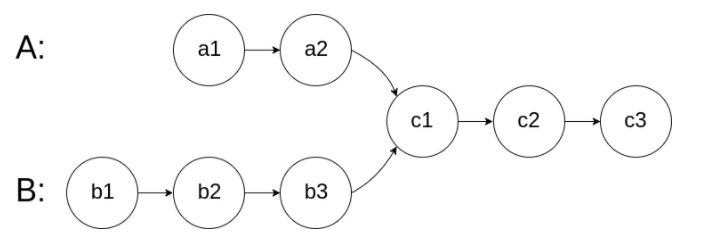
2. 题目解析：相交链表这题由于链表 A 和链表 B 的长度差原因，必须消除长度差因素。可以采用暴力法，哈希表法，但时间复杂度和空间复杂度都较高，这里推荐一种双指针解法。代码如下：

public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        if(headA == null || headB == null)
            return null;
        ListNode p = headA;
        ListNode q = headB;
        while(p != q){
            p = p == null ? headB : p.next;
            q = q == null ? headA : q.next;
        }
        return p;
    }
}

零钱兑换

1. 题目：给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额，返回 -1。你可以认为每种硬币的数量是无限的。

   输入：coins = [1, 2, 5], amount = 11
   输出：3 
   解释：11 = 5 + 5 + 1
   

2. 题目解析：很明显的背包问题（动态规划求解），需要找出动态转移方程即可。

class Solution {
    public int coinChange(int[] coins, int amount) {
        int []dp = new int[amount + 1];
        Arrays.fill(dp, amount + 1);
        dp[0] = 0;
        //i 表示钱包，即钱包中的总金额为 i
        for(int i = 0; i < amount + 1; i ++){
            for(int j = 0;j < coins.length; j ++){
                if(coins[j] <= i){
                    //动态转移方程即是从 i - coin 的状态放入 coin 元硬币转换为现在的状态
                    dp[i] = Math.min(dp[i], dp[i - coins[j]] + 1);
                }
            }
        }
        return dp[amount] > amount ? -1 : dp[amount];
    }
}

戳气球

1. 题目：有 \(n\) 个气球，编号为 0 到 \(n - 1\)，每个气球上都标有一个数字，这些数字存在数组 nums 中。现在要求你戳破所有的气球。戳破第 \(i\) 个气球，你可以获得 nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。 这里的 i - 1 和 i + 1 代表和 i 相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界，那么就当它是一个数字为 1 的气球。求得戳破气球所能获得的最大数量硬币。

2. 题目解析：题目很明显可以用动态规划来做。但首先要注意一点，当数组下标越界时需要用 1 去替代 \(i + 1\) 和 \(i - 1\) 的值，因此，最好用一个数组来存放相关值。另外，相邻元素由于戳破气球时，会导致原本不相邻的元素变为相邻的元素，因此，可以将戳破气球的过程逆向思维思考，变成添加气球，那么左右相邻边界变得更为容易思考。可以采用记忆搜索的方式或者自底向上的动态规划的方式，代码如下：

class Solution {
    // val 数组存放第 i 元素之前的元素
    public int[] val;
    // rec 二维数组存放左右边界为下标时的硬币数量，动态规划方式计算的。
    public int[][] rec;

    public int maxCoins(int[] nums) {
        int n = nums.length;
        val = new int[n + 2];
        rec = new int[n + 2][n + 2];
        for(int i = 1; i <= n; i ++)
            val[i] = nums[i - 1];
        val[0] = 1;
        val[n + 1] = 1;
        for(int i = 0;i < n + 2; i ++){
            for(int j = 0; j < n + 2; j ++){
                rec[i][j] = -1;
            }
        }
        return getMax(0, n + 1);
    }

    public int getMax(int left, int right){
        if(left >= right - 1)
            return 0;
        //避免递归时动态规划的多次搜索，直接返回相应的值
        if(rec[left][right] != -1)
            return rec[left][right];
        for(int i = left + 1; i < right; i ++){
            int sum = val[left] * val[i] * val[right];
            sum += getMax(left, i) + getMax(i, right);
            rec[left][right] = Math.max(sum, rec[left][right]);
        }
        return rec[left][right];
    }
}

class Solution {
    public int maxCoins(int[] nums) {
        int n = nums.length;
        int []val = new int[n + 2];
        int [][]rec = new int[n + 2][n + 2];
        for(int i = 1; i <= n; i ++)
            val[i] = nums[i - 1];
        val[0] = 1;
        val[n + 1] = 1;
        /**
        * 尤其注意循环的嵌套关系，先是 i 从 n - 1，自底向上的动态规划，主要原因是由于 i < k < j，假如自顶向	   
        * 下，会导致计算 dp[k][j] 时先引入还未计算的值，使得最后产生的值是错误的，主要思想其实和方法一十分相          
        * 似，不过方法一更好理解
        **/
        for(int i = n - 1; i >= 0; i --){
            for(int j = i + 2; j <= n + 1; j ++){
                for(int k = i + 1; k < j; k ++){
                    int sum = val[i] * val[k] * val[j];
                    sum += rec[i][k] + rec[k][j];
                    rec[i][j] = Math.max(rec[i][j], sum);
                }
            }
        }
        return rec[0][n + 1];
    }
}