[题解] P7514 [省选联考 2021 A/B 卷] 卡牌游戏

P7514 [省选联考 2021 A/B 卷] 卡牌游戏

一个考场上差点想到正解的提，要是想到了就A了。

有思路一定要想下去！！

贪心做法

首先我们要明白：

• 翻的卡牌一定是一段后缀和一段前缀。（可能为空）

考场上想过能不能双指针贪心，后来发现不好处理。

在 \(a\) 数组单调的情况下，翻中间的卡牌没有翻两边的卡牌优。

• 翻的次数是有限制的。

我们解决的问题就是如何分配这 \(m\) 次机会给前缀后缀

值得一提的是，有一个 \(O(n+m^2)\) 的做法，可以拿到 \(60pts\)

• 预处理出取 \(i\) 个后缀的最大值和最小值 \(fmax_i\ and \ fmin_i\) ，同样再处理出取 \(j\) 个前缀的最大值和最小值 \(gmax_i \ and \ fmin_i\)
• 暴力枚举 \(m=i+j\) 的组合方式

我个人感觉这就是贪心的优化：

如何避免盲目枚举？不难发现

• \(f\) 数组是单调递减的（如果翻了当前的不优，会继承上一个答案）

• \(g\) 数组是单调递增的

可以考虑预处理 \(f\) 后计算 \(g\) 的时候统计答案

于是问题变成了如何分配后缀翻的数量使得答案更优。

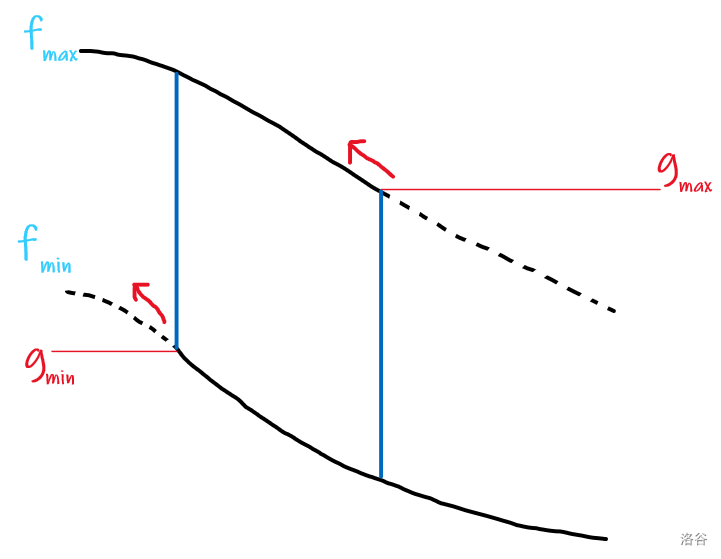
嫖了一张图

• 显然在两个交点的位置之一答案最优

• 如果最大和最小值都取 \(f\) 的话前缀不翻肯定优，这在处理 \(f\) 时可以维护。

由于 \(gmax_i\) 是单调不降的，这里理解一下：

因为翻前缀的目的只是为了使得最小值尽量大，所以翻的卡牌一定是全局最小值，可以有以下两种情况：

1. 翻的卡牌变成了最大值，单调递增
2. 翻的卡牌没有影响到最大值

类似地，\(f\) 数组翻的卡牌一定是全局最大值

所以 \(fmin_i\) 是单调不增的。

这既证明了图像的正确性，也证明了算法的正确性。

---

代码实现

由于 \(gmax\) 和 \(gmin\) 都是单调不降的，所以需要维护这两个点。

还有需要注意的就是，当前如果处理到了 \(g[j]\) 的话，\(f\) 最多选 \(m-j\) 个，需要强行移动

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cctype>
using namespace std;
inline int read(){
    char c=getchar();int x=0;
    while(!isdigit(c))c=getchar();
    while(isdigit(c)){
        x=(x<<3)+(x<<1)+(c^48);
        c=getchar();
    }
    return x;
}
const int maxn = 1e6 + 10;
int a[maxn],b[maxn],f[maxn][2],g[maxn][2];
int n,m;
inline int calc(int i,int j){
    return max(g[i][0],f[j][0])-min(g[i][1],f[j][1]);
}
int main(){
    n=read();m=read();
    for(int i=1;i<=n;i++)a[i]=read();
    for(int i=1;i<=n;i++)b[i]=read();
    int mx=-1,mn=0x7fffffff;
    int ans=a[n]-a[1];
    f[0][0]=a[n];f[0][1]=0x7fffffff;
    for(int i=n,k=1;i>n-m;i--,k++){
        mx=max(mx,b[i]);mn=min(mn,b[i]);
        f[k][0]=max(mx,a[i-1]);f[k][1]=min(mn,a[i-1]);
        if(f[k][0]>f[k-1][0])f[k][0]=f[k-1][0],f[k][1]=f[k-1][1];
        ans=min(ans,f[k][0]-min(a[1],f[k][1]));//只翻后缀
    }
    mx=-1,mn=0x7fffffff;
    int pmx=m-1,pmn=m-1;
    for(int i=1;i<=m;i++){
        mx=max(mx,b[i]);mn=min(mn,b[i]);
        g[i][0]=max(mx,a[i+1]);g[i][1]=min(mn,a[i+1]);
        if(g[i][1]<g[i-1][1])g[i][1]=g[i-1][1],g[i][0]=g[i-1][0];
        //前缀选i个
        pmx=min(pmx,m-i);
        pmn=min(pmn,m-i);
        while(pmx && f[pmx-1][0]<=g[i][0])pmx--;
        while(pmn && f[pmn-1][1]<=g[i][1])pmn--;
        ans=min(ans,calc(i,pmx));
        ans=min(ans,calc(i,pmn));
    }
    printf("%d\n",ans);
    return 0;
}