P5244 [USACO19FEB] Mowing Mischief P

搬题的时候遇到的一道好题。

题目大概是这个意思：让你选一个点集，使得对于任意两个点，\(x_p < x_q\) 等价于 \(y_p < y_q\).

要求在最大化选点个数的前提下最小化按 \(x\) 排序后，相邻两点为对角线构成的长方形面积之和。

大概可以看作是 \(n \leq 10^5\).

---

看到这题就傻了，这题怎么做？

冷静一下发现这个限制是个二维 LIS. 也就是说，按照 \(x\) 排序后可以求出 \(y\) 的 \(LIS\)，转移要满足 \(l_i = l_j + 1\).

这是这个题神仙的第一步：转移构成分层图关系。因此，可以看作 \(l_i\) 相同的在一起转移。

先把 \(dp\) 方程写出来：

\[dp_{i} = \min_{l_i = l_j + 1, x_j \leq x_i, y_j \leq y_i} dp_{j} + (x_i - x_j)(y_i - y_j) \]

这个限制非常神必。看起来是个三维偏序，拿头优化？

这是这个题神仙的第二步：一层的点假如 \(x_p < x_q\)，那一定有 \(y_p > y_q\). 否则肯定不是同层。

这是这个题神仙的第三步：在上述步骤的加持下，\(dp\) 在层之间有决策单调性。

这是为啥？

我们回顾下四边形不等式的内容。对于 \(x_1 < x_2, y_1 < y_2\)，若 \(w(x_1, y_1) + w(x_2, y_2)\) 比 \(w(x_1, y_2) + w(x_2, y_1)\) 要优，那么转移方程满足四边形不等式。

我们来看下在这个例子里对应的是什么：

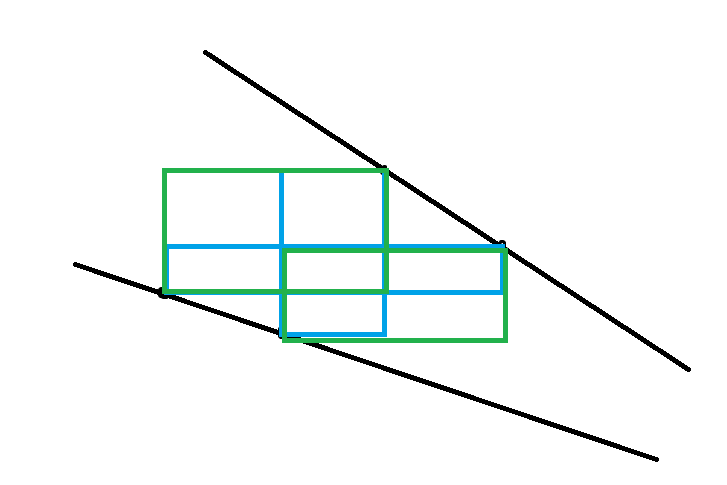
我们发现决策单调性是显然的。这样就可以用线段树分治优化决策单调性了。