NOI2019

NOI2019 D1T3 序列

先来谈谈部分分。本题的 28 分和 40 分的部分分都是给 dp. 其中 28 分的 dp 是白给的，40 分的 dp 需要注意到我们是对【集合】做 dp，可以利用【集合的无序性】进行一些操作，省掉某一些维度。

例如在本题中，我们强制要选 \(K\) 个 \(a\)，假如我们先选了 \(L\) 对 \(AB\) 和 \(K-L\) 个 \(B\)，选取的 \(A\) 假如从大到小排序，一定是一段连续的前缀。因此，我们只需要记录 \(AB\) 选的个数和 \(B\) 选的个数，从而推断出 \(A\) 选不选进行转移即可，复杂度变为 \(O(n^3)\).

接下来有 2 种优化途径：模拟费用流，凸优化。

一. 模拟费用流

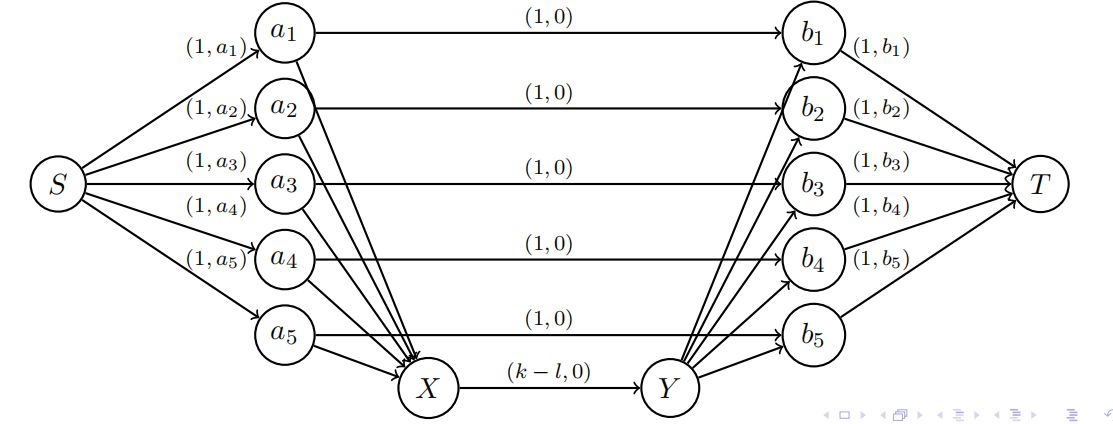
模拟费用流，一般都是从退流的角度出发，少数题目从反向边的角度出发。但是这题假如你用反向边的角度，你就相当于自己缠住了自己的脚——因为这题内部的反向边错综复杂。

有一个特别特别好的性质：费用流不会增广出环。假如增广出负环，那这题没法做。假如增广出正环，就不是最短路。所以：每次增广，必然只与 \(1\) 个 \(a\) 和 \(1\) 个 \(b\) 相关。否则就会增广出环，这显然不是我们所想要的。

同时，还有一个特别特别好的性质：中间的那坨边费用全是 \(0\). 这意味着我们不需要担忧中间的具体结构，只需要关心对于每对可能会增广的 \((i, j)\)， \(i\) 和 \(j\) 是否能够到达。这与什么有关呢？这仅仅与 \(X \to Y\) 边的流量，和 \(i, j\) 自己的 \((1, 0)\) 边是否被封堵相关。

最后，还有一个特别特别好的性质，我们只需要记录哪些 \(a_i, b_j\) 有流，而 \(X \to Y\) 的流量我们是可以推断的——一定是总流量减掉 \((a_i, b_i)\) 的对数，因为这样一定是最优的。所以我们只需要这轮是谁增广，然后我们动态判一下 \((a_i, b_i)\) 是否都有流即可。

综合以上来看，有 \(5\) 种情况：

两个 \(a_i, b_i\) 直接配上了。
一个 \(a_i\) 和一个 \(b_j\) 通过 \(X \to Y\) 边配上了。
一个 \(a_i\) 和一个 \(b_j\) 通过 \(X \to Y\) 边配上了，原来 \(b_j\) 对面的 \(a_j\) 已经有的连了。
一个 \(a_i\) 和一个 \(b_j\) 通过 \(X \to Y\) 边配上了，原来 \(a_i\) 对面的 \(b_i\) 已经有的连了，同 \(3\).
一个 \(a_i\) 和一个 \(b_j\) 通过 \(X \to Y\) 边配上了，原来两边都有的连了。

其实 \(3,4\) 情况等价，不过这里就写两遍，麻烦一点就是清楚一点。

以上 \(5\) 种情况可以用可删除堆维护。具体如下：


		维护 5 个堆，分别为 L0, L0match, R0, R0match, LR0.
		L0s 表示左侧所有”右边对应点已经被匹配” 且暂时空余的点。
		L0 表示左侧所有空余的点（包含 L0s）。
		L1s 表示右侧所有”左边对应点已经被匹配” 且暂时空余的点。
		L1 表示右侧所有空余的点（包含 L1s）。
		LR0 表示左右侧同时空余的点。