一、插值
插值:从已知点近似计算未知点的近似计算方法
1.一维插值函数
y=interp1(x0,y0,x,'method');
其中 x0,y0 是已知数据点,x 是插值点,y 是插值点的函数值
mothod默认为线性插值,其值可为:
‘nearest’ 最近项插值
‘linear’ 线性插值
‘spline’ 三次样条插值 (还可直接spline(x0,y0,x))
‘cubic’ 立方插值/三次Hermite多项式插值(新版本改为pchip)
注:
①所有的插值方法要求x0是单调的
②被插值节点不能超出x0范围
③若y0为矩阵,则对y0的每一列进行插值,x可以为向量
Matlab 中三次样条插值也有现成的函数:
y=spline(x0,y0,x);
pp=csape(x0,y0,conds);
pp=csape(x0,y0,conds,valconds);y=ppval(pp,x)
其中 x0,y0 是已知数据点,x 是插值点,y 是插值点的函数值
注:使用csape函数求插值点的函数值,必须调用函数 ppval。
例:机床加工
待加工零件的外形根据工艺要求由一组数据(x,y) 给出(在平面情况下),用程控铣床加工时每一刀只能沿 x方向和 y 方向走非常小的一步,这就需要从已知数据得到加工所要求的步长很小的坐标(x,y)。
下表中给出的(x,y)数据位于机翼断面的下轮廓线上,假设需要得到 x坐标每改变 0.1 时的 y 坐标。试完成加工所需数据,画出曲线,并求出 0 =x 处的曲线斜率和 13 ≤x≤ 15 范围内 y 的最小值。
要求用分段线性和三次样条三种插值方法计算。
|
x |
0 |
3 |
5 |
7 |
9 |
11 |
12 |
13 |
14 |
15 |
|
y |
0 |
1.2 |
1.7 |
2.0 |
2.1 |
2.0 |
1.8 |
1.2 |
1.0 |
1.6 |
解:
x0=[0 3 5 7 9 11 12 13 14 15];
y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];
x=0:0.1:15;
y1=interp1(x0,y0,x);%默认的插值方法:线性插值
y2=interp1(x0,y0,x,'spline');%三次样条插值
pp1=csape(x0,y0);%三次样条插值,使用默认边界条件即Lagrange边界条件
y3=fnval(pp1,x);%求被插值点函数值
pp2=csape(x0,y0,'second');%三次样条插值,边界为二阶导数
y4=fnval(pp2,x);
%画图
subplot(1,4,1)
plot(x0,y0,'*',x,y1)
title('分段线性插值')
subplot(1,4,2)
plot(x0,y0,'*',x,y2)
title('三次样条插值')
subplot(1,4,3)
plot(x0,y0,'*',x,y3)
title('三次样条插值(Lagrange)')
subplot(1,4,4)
plot(x0,y0,'*',x,y4)
title('三次样条插值(Second)')
%因三次样条插值曲线光滑,故采用y3计算斜率
%近似计算每一点的斜率
dx=diff(x);
dy=diff(y3);
dy_dx=dy./dx;
%求x=0处斜率(即dy_dx计算的斜率中的第一个元素)
dy_dx0=dy_dx(1)
%求[13,15]范围内最小值
ytemp=y3(131:151);
ymin=min(ytemp);
index=find(y3==ymin);
xmin=x(index);
[xmin,ymin]
图像如图
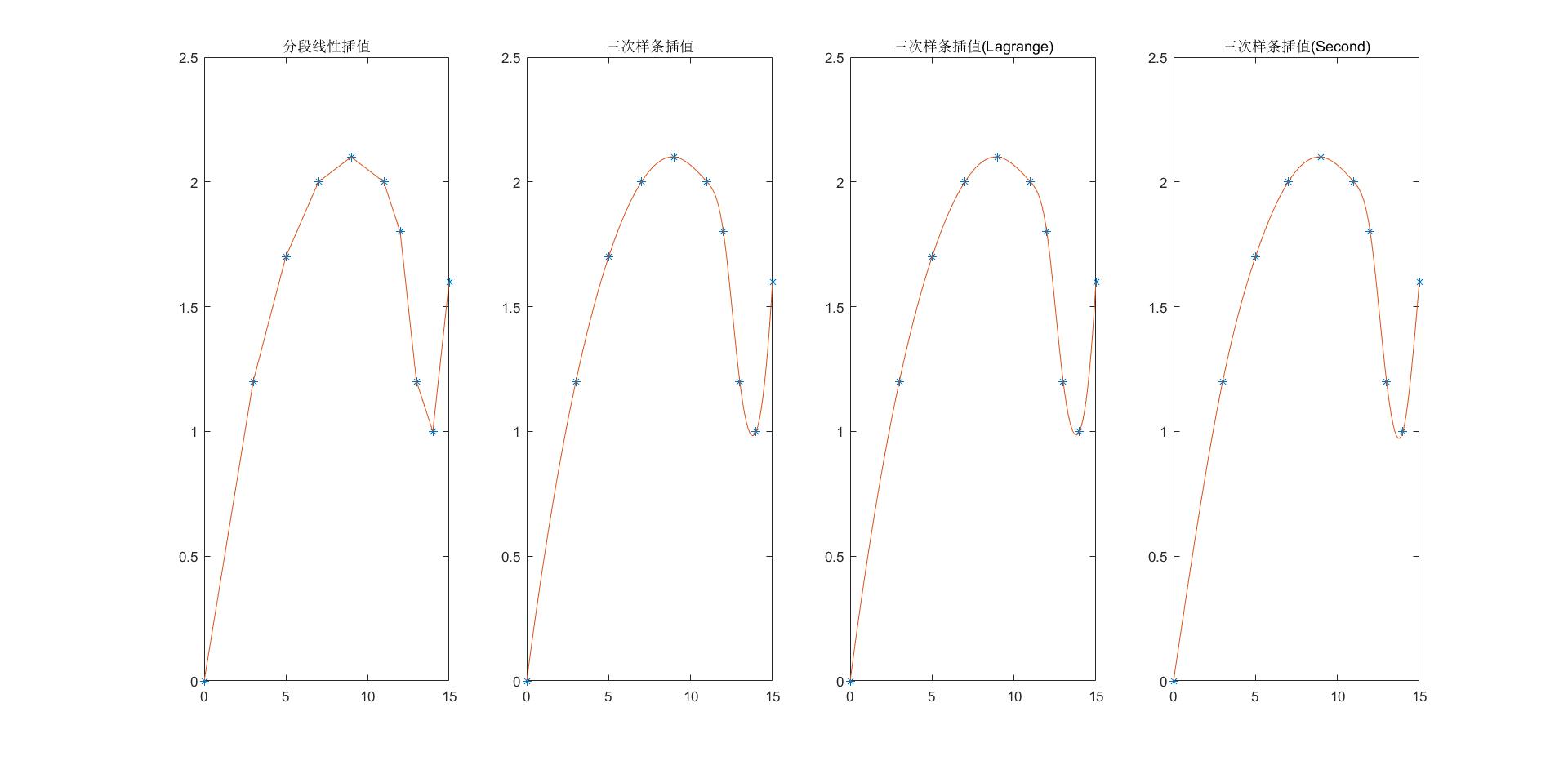
可以看出,分段线性插值的光滑性较差。
得到计算结果为:
dy_dx0 =
0.4972
ans =
13.8000 0.9851
2.二维插值函数
1)插值节点为网格节点
z=interp2(x0,y0,z0,x,y,'method')
其中 x0,y0 分别为m 维和n维向量,表示节点,z0 为 m *n 维矩阵(按照表格原样输入就行),表示节点值,x,y 为一维数组,表示插值点。
注:
①x与y应是方向不同的向量,即一个是行向量,另一个是列向量
②z 为矩阵,它的行数为 y 的维数,列数为 x的维数,表示得到的插值
③'method' 的用法同上面的一维插值。
三次样条插值,还可用命令:
pp=csape({x0,y0},z0,conds,valconds),z=fnval(pp,{x,y})
其中 x0,y0 分别为m 维和n维向量,z0 为 n*m 维矩阵(表格数据需要进行转置),z 为矩阵,它的行数为x的维数,列数为y的维数,表示得到的插值,具体使用方法同一维插值。
例:在一丘陵地带测量高程,x和 y 方向每隔100米测一个点,得高程如2表,试插 值一曲面,确定合适的模型,并由此找出最高点和该点的高程。
|
y x |
100 |
200 |
300 |
400 |
500 |
|
100 |
636 |
697 |
624 |
478 |
450 |
|
200 |
698 |
712 |
630 |
478 |
420 |
|
300 |
680 |
674 |
598 |
412 |
400 |
|
400 |
662 |
626 |
552 |
334 |
310 |
解:
x0=100:100:500;
y0=100:100:400;
z0=[636 697 624 478 450;698 712 630 478 420;680 674 598 412 400;662 626 552 334 310];
x=100:1:500;
y=100:1:400;
%采用interp2函数进行二维插值时,插值点中x,y应是方向不同的向量,故转置
y=y';
z2=interp2(x0,y0,z0,x,y,'spline');
mesh(x,y,z2)
title('二维三次样条插值')
%求最高点地址
[i j]=find(z2==max(max(z2)));
%求最高点坐标
res_x=x(i)
res_y=y(j)
zmax=z2(i,j)
图像如图
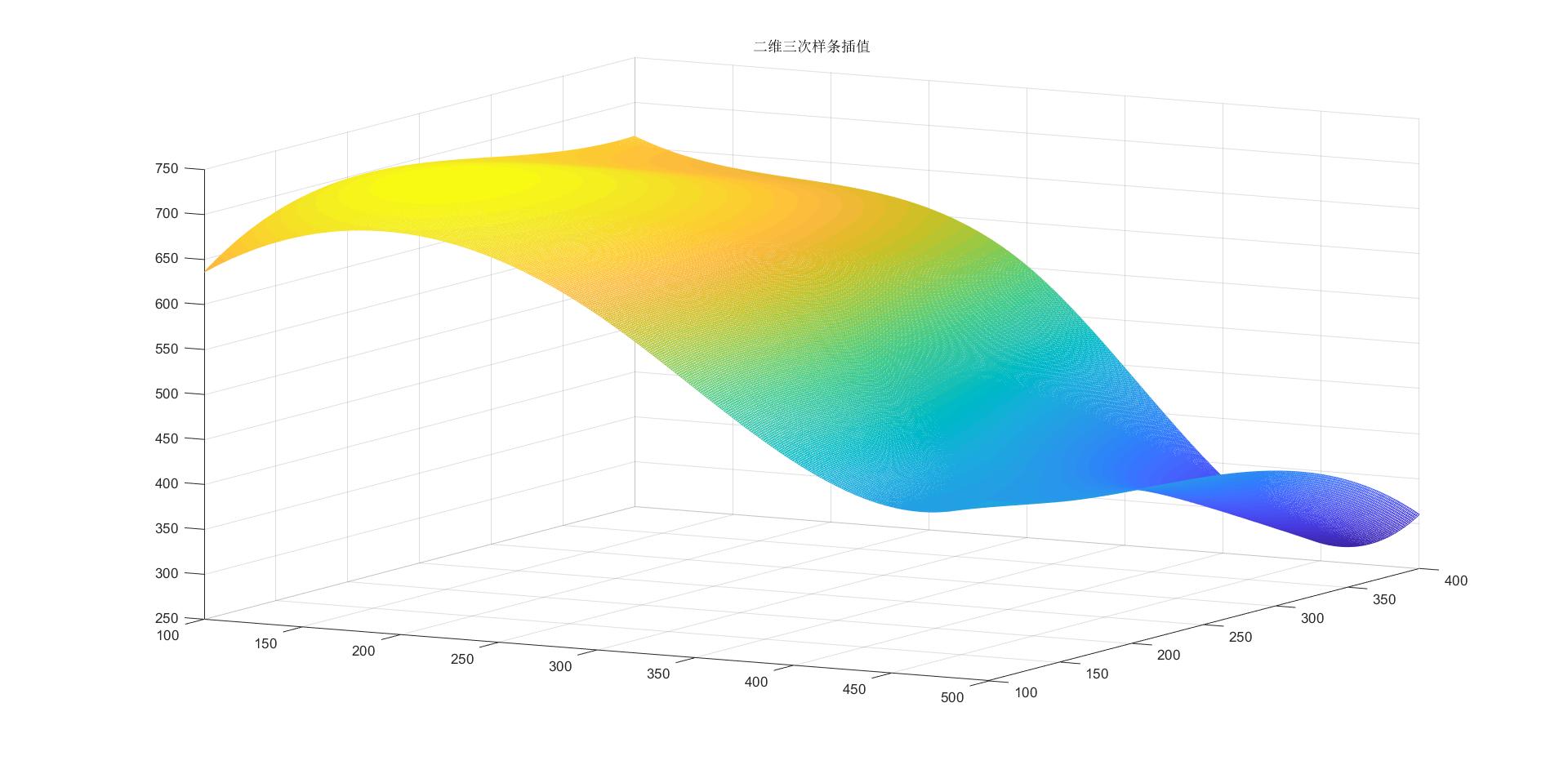
结果:
res_x =
175
res_y =
170
zmax =
719.7716
2)插值节点为散点
ZI = griddata(x,y,z,XI,YI)
其中 x、y、z均为 n 维向量。向量XI、 YI 是给定的网格点的横坐标和纵坐标,返回值 ZI 为网格(XI,YI)处的函数值。XI 与 YI 应是方向不同的向量,即一个是行向量,另一个是列向量.
例: 在某海域测得一些点(x,y)处的水深 z 由下表给出,在矩形区域内画出海底曲面的图形。
|
x |
129 |
140 |
103.5 |
88 |
185.5 |
195 |
105 |
157.5 |
107.5 |
77 |
81 |
162 |
162 |
117.5 |
|
y |
7.5 |
141.5 |
23 |
147 |
22.5 |
137.5 |
85.5 |
-6.5 |
-81 |
3 |
56.5 |
66.5 |
84 |
-33.5 |
|
z |
4 |
8 |
6 |
8 |
6 |
8 |
8 |
9 |
9 |
8 |
8 |
9 |
4 |
9 |
解:
x=[129 140 103.5 88 185.5 195 105 157.5 107.5 77 81 162 162 117.5]; y=[7.5 141.5 23 147 22.5 137.5 85.5 -6.5 -81 3 56.5 -66.5 84 -33.5]; z=[4 8 6 8 6 8 8 9 9 8 8 9 4 9]; %求x和y的最大值和最小值,便于定xi和yi的范围 xmm=minmax(x) ymm=minmax(y) xi=xmm(1):xmm(2); yi=ymm(1):ymm(2); zi1=griddata(x,y,z,xi,yi','cubic');%立方插值 zi2=griddata(x,y,z,xi,yi','nearest');%最近点插值 zi=zi1; zi(isnan(zi1))=zi2(isnan(zi1));%将立方插值中的不确定值换成最近点插值的结果 %画图 mesh(xi,yi,zi)
图像:
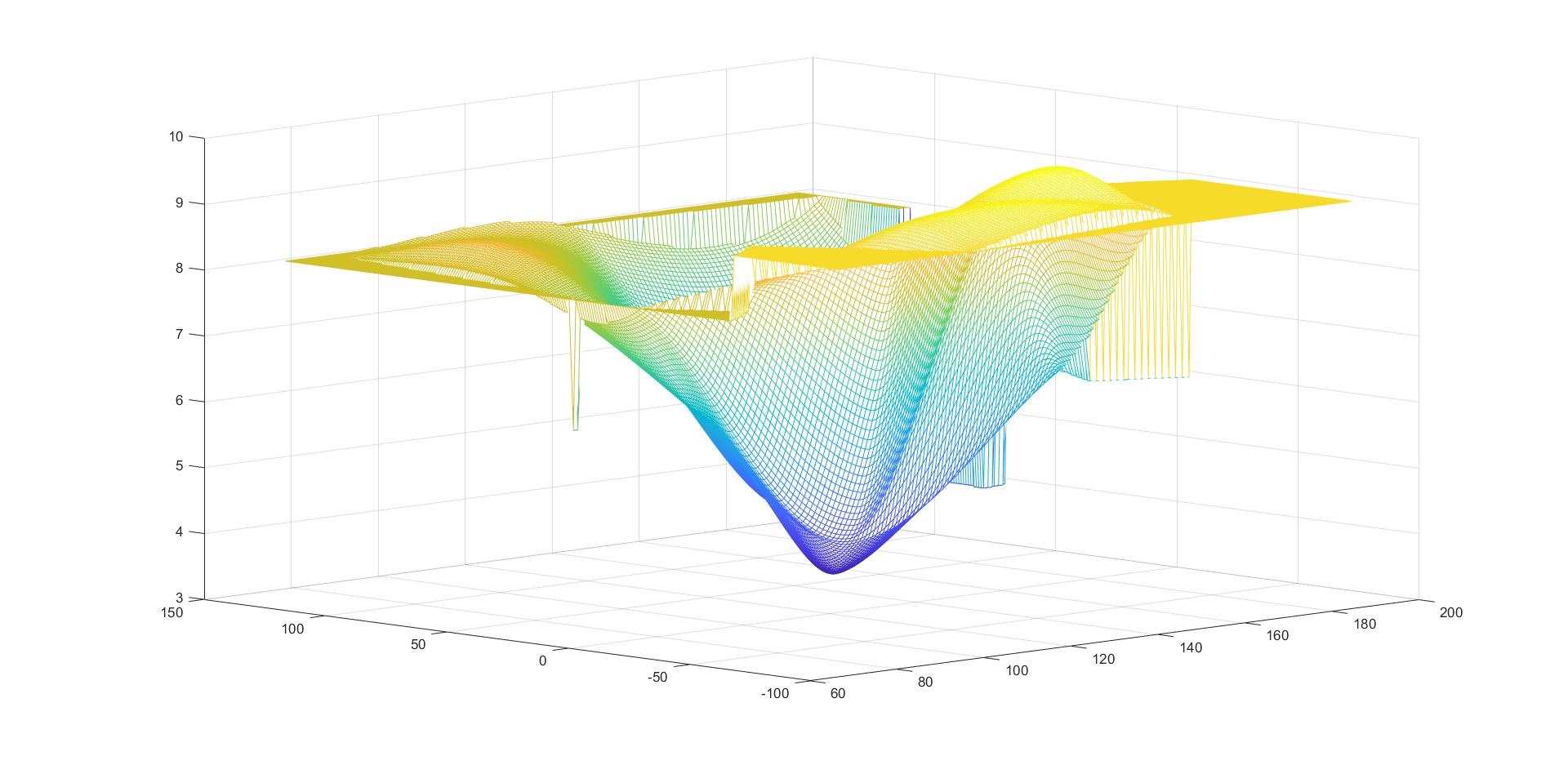
二、拟合
拟合:已知平面上的n个点互不相同,寻求一个函数f(x)在某种准则下,使f(x)所有数据点最为接近。(不要求过已知数据点)
1.多项式拟合
a=polyfit(x,y,m)
其中输入参数x,y为要拟合的数据,m 为拟合多项式的次数,输出参数 a 为拟合多项式的系数。
注:当使用polyfit进行拟合时,多项式的阶次最大不超过length(x)-1
求多项式在 x 处的值 y 可用:
y=polyval(a,x)
例: 用最小二乘法求一个形如的公式,使它与下表所示的数据拟合。
|
x |
19 |
25 |
31 |
38 |
44 |
|
y |
19.0 |
32.3 |
49.0 |
73.3 |
97.8 |
解:
x=[19 25 31 38 44];
y=[19.0 32.3 49.0 73.3 97.8];
a=polyfit(x,y,2)
%设步长为0.1,进行画图
x0=19:0.1:44;
y0=polyval(a,x0);
plot(x,y,'*',x0,y0,'r')
图像如图:
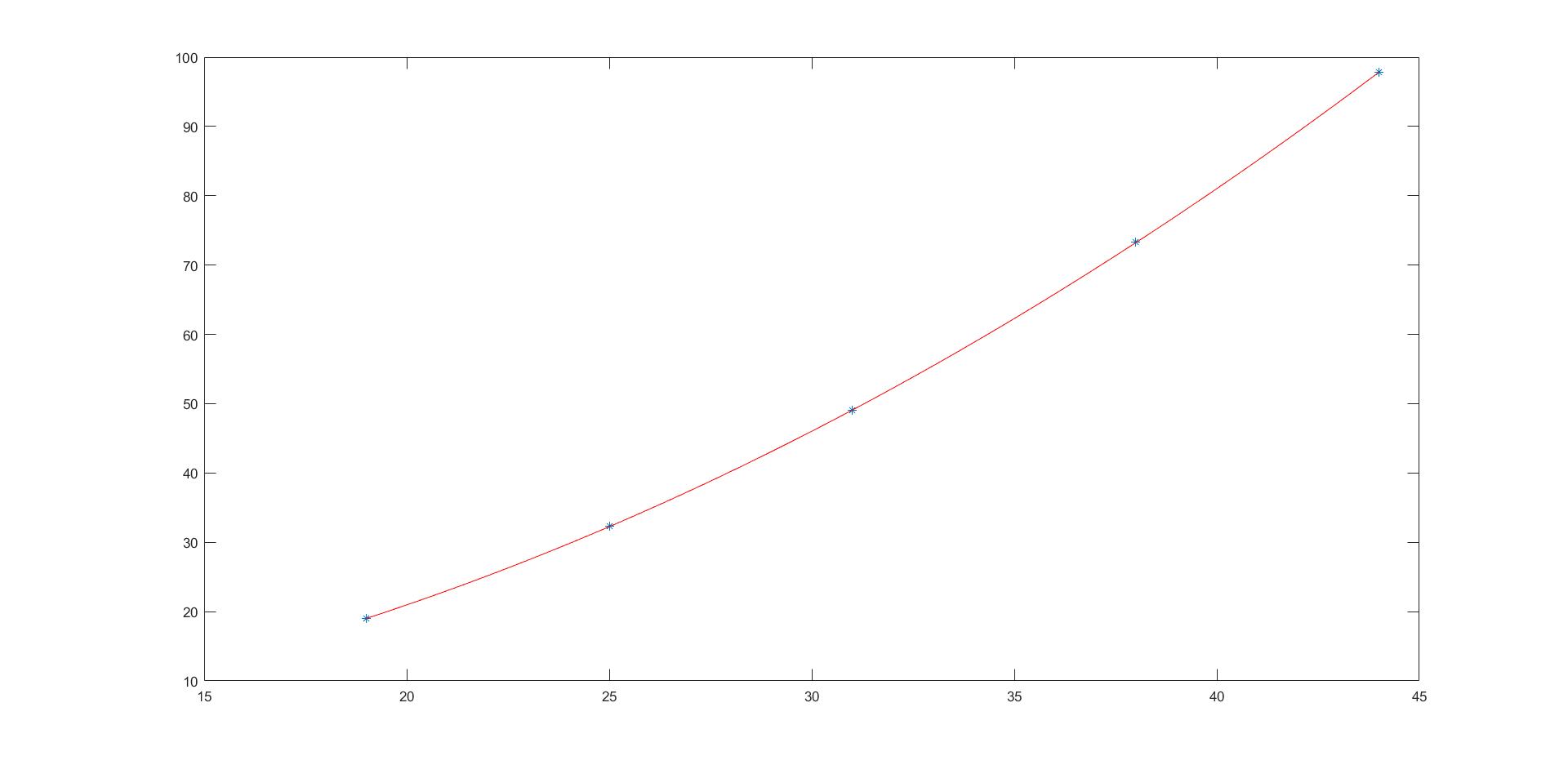
结果为:![]()
2.非线性拟合: 已知输入向量xdata和输出向量ydata,并且知道输入与输出的函数关系为ydata=F(x, xdata),但不知道系数向量x。今进行曲线拟合,求x使得输出的如下最小二乘表达式成立:![]()
在MATLAB中,可用函数lsqcurvefit和lsqnonlin 解决此类问题
lsqcurvefit 函数:
x= lsqcurvefit (‘fun’,x0,xdata,ydata,options)
其中fun是定义函数F(x,data)的M文件,x0为初始解向量,xdata,ydata为满足关系ydata=F(x,xdata)的数据
lsqnonlin 函数:
x= lsqnonlin (‘fun’,x0,options)
参数说明同上
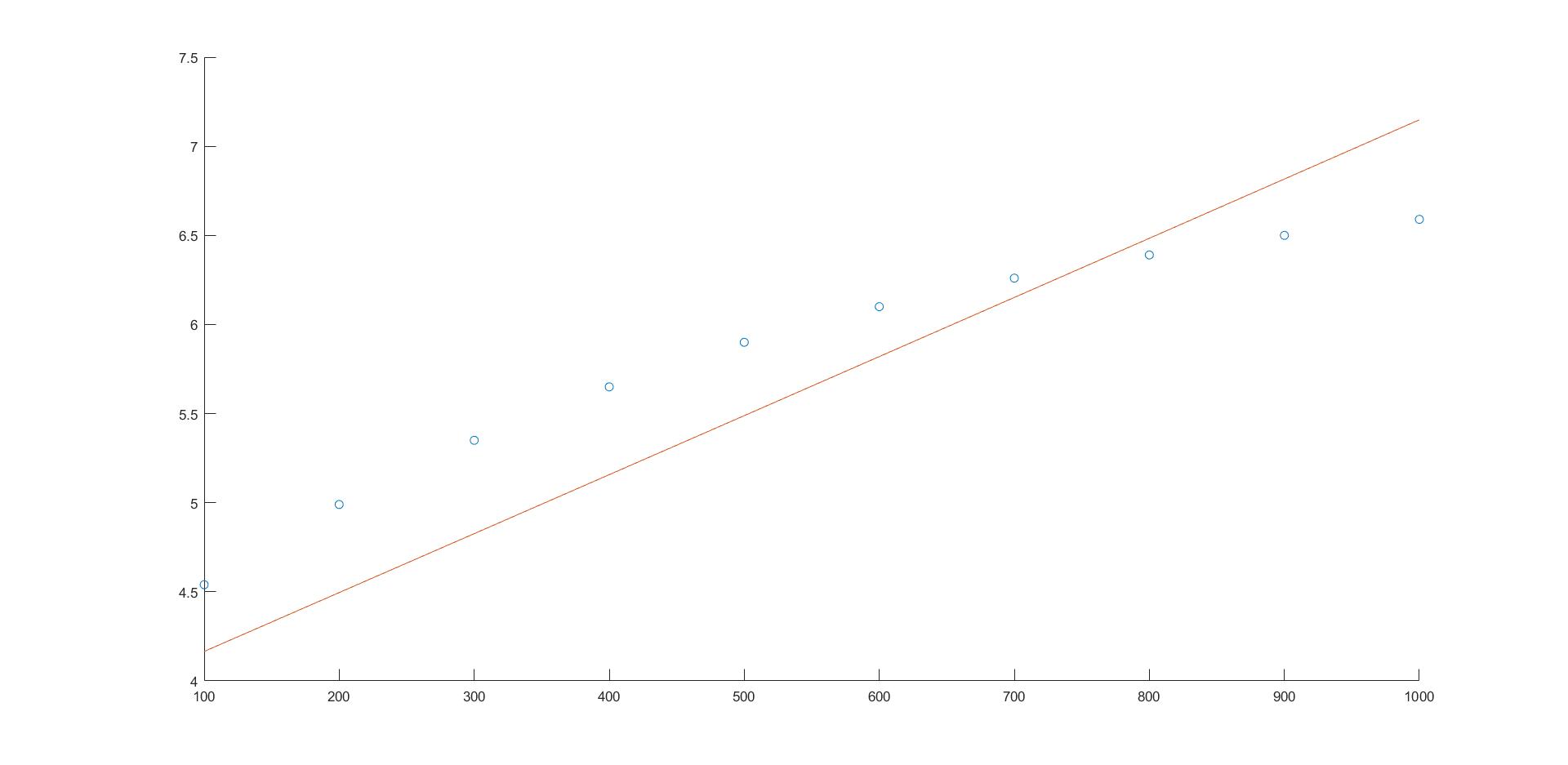
例:用下面表中的数据拟合函数中的参数a,b,k。
|
t |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
|
c |
4.54 |
4.99 |
5.35 |
5.65 |
5.90 |
6.10 |
6.26 |
6.39 |
6.50 |
6.59 |
解:首先编写 M 文件myfun.m 定义函数F(x,xdata):
function f=myfun(x,tdata);
% x(1)=a,x(2)=b,x(3)=k
f=x(1)+x(2)*exp(-0.02*x(3)*tdata);
然后调用函数 lsqcurvefit
=100:100:1000;
c=[4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59];
x0=[0.01 0.02 0.01];%初始解向量随便取的
x=lsqcurvefit(@myfun,x0,t,c)
%作图查看拟合效果
scatter(t,c)
hold on
c1=myfun(x,t);
plot(t,c1)
hold off
图像:
参考文献:
司守奎,孙兆亮,数学建模算法与应用(第二版),北京.国防工业出版社,2019
刘浩,韩晶,MATLAB R2018a完全自学一本通,中国工信出版集团,2019


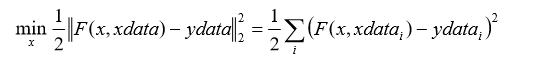
 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号