建立Huffman树的基本思路:给定有权重的一系列数据(带权重),从中挑选最小权重的两个数据,组成一棵树,得到的父节点再插入到数据系列当中。
开始的时候按着严老师的办法,是借助顺序表来完成Huffman树的建立;同样,在建树过程中要从顺序表中选择比较小的两个数,相加后再插入到表尾,如此往复,知道所有给出的点都插入为止。
通过最小堆来建树也很灵活便捷。堆的性能高,排序时间复杂度为nlog(2)n,利用最小堆,就可以将很快找出最小的元素(总是在顶部)。
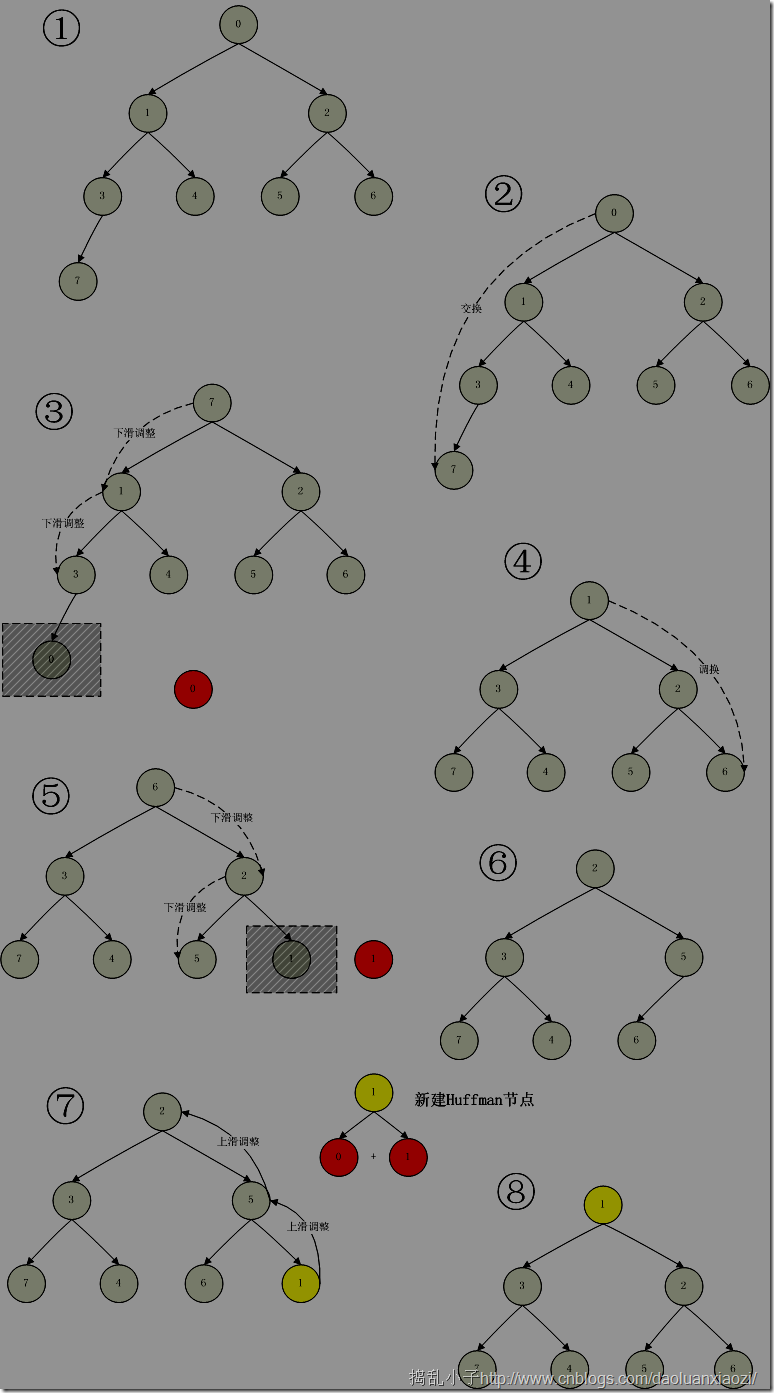
下面8步立刻掌握利用最小堆来建立Huffman树。
看图解说
①原图(已经是最小堆);
②交换堆的首元素(肯定是最小的)和最后一个元素对换;
③交换后删除最后一个元素(复制出来),其实也不是真正的删除,只是size-1这个操作而已;调换后就不是堆了,重新调整heap为最小堆,调整可以用递归调用,也可以用下标作为判断条件,我的代码用的是下标判断条件;
④继续②;
⑤弹出最小的,调整;将两个最小点复制出来后,组成新的父节点,调整他们之间的内部指针关系;
⑥调整后;
⑦插入新节点,调整;
⑧调整后。
以上做了第一遍的操作,继续做下去知道堆中只剩下最后一个元素为止,再将root指向其就可以了,下面是代码。如此下来,Huffman树就建好了。
Huffman节点数据结构设计:
#ifndef _HUFFMANNODE_H_#define _HUFFMANNODE_H_struct HuffmanNode //Huffman节点定义{private: int data;public: //构造函数 HuffmanNode * left,* right,* parent; HuffmanNode():left(NULL),right(NULL),parent(NULL),data(-1){} HuffmanNode(int d):left(NULL),right(NULL),parent(NULL),data(d){} //重载运算符 HuffmanNode &operator=(const HuffmanNode& hn) { left = hn.left; right = hn.right; data = hn.data; return *this; } //数据的获取和维护 int GetData()const{return data;} //获取数据 bool SetData(int d){data = d;return true;} //设置数据};#endif |
最小堆类:
#include <iostream>using namespace std;#ifndef _MINHEAP_H_#define _MINHEAP_H_#include "HuffmanNode.h"const int DefaultSize = 100;class MinHeap{ HuffmanNode * heap; int szCurrent;public: MinHeap(int sz = DefaultSize); ~MinHeap() {delete [] heap;} void CreateMinHeap(int arr[],int n); //数组构建最小堆 bool Insert(HuffmanNode * e); //往堆中插入Huffman节点 void SiftDown(int start,int m); //下滑,重建最小堆 void SiftUp(int start,int m); //上滑,在插入的时候用到 HuffmanNode * GetMinNode(); //获取Huffman节点data值最小的节点,同时维护szCurrent bool SwapNode(int i,int j); //交换下标为i和j的Huffman节点 void Print(); //打印Huffman节点};#endif#include <iostream>using namespace std;#include "MinHeap.h"#include <assert.h>MinHeap::MinHeap(int sz){ heap = new HuffmanNode[sz]; assert(heap!=NULL); szCurrent = 0;}void MinHeap::CreateMinHeap(int arr[],int n){ this->heap = new HuffmanNode[DefaultSize]; assert(heap!=NULL); int i; for(i=0; i<n; i++) heap[i].SetData(arr[i]); szCurrent = n; int currentpos = (szCurrent-2)/2; //从最后一个顶点开始调整 while(currentpos >= 0) { SiftDown(currentpos,szCurrent-1); currentpos -- ; }}void MinHeap::SiftDown(int start,int m){ int i = start,j = i*2+1; HuffmanNode temp = heap[i]; while(j<=m) { if(j<m && heap[j].GetData() > heap[j+1].GetData()) //j记录比较小的子节点 j++; if(temp.GetData() <= heap[j].GetData()) //不调整 break; else { heap[i] = heap[j]; //子节点上移 i = j; j = 2*j+1; } } heap[i] = temp;}void MinHeap::SiftUp(int start,int m){ int j = start, //子节点位置 i = (start-1) / 2; //顶点位置 HuffmanNode temp = heap[j]; //记录子节点 while(j > 0) { if(temp.GetData() > heap[i].GetData()) //不调整 break; else { heap[j] = heap[i]; //顶点下滑 j = i; i = (i-1) / 2; } } heap[j] = temp;}void MinHeap::Print(){ for(int i=0; i<szCurrent; i++) cout << heap[i].GetData() << " "; cout << endl;}bool MinHeap::Insert(HuffmanNode * e){ szCurrent++; if(szCurrent > DefaultSize) abort(); heap[szCurrent-1] = *e; SiftUp(szCurrent-1,0); //调整 return true;}HuffmanNode * MinHeap::GetMinNode(){ if(szCurrent>0) { HuffmanNode * t; SwapNode(0,szCurrent-1); //此时heap[0].data是最小的,让它跟最后一个元素调换 szCurrent--; SiftDown(0,szCurrent-1); t = new HuffmanNode(); * t = heap[szCurrent]; cout << "GetMinNode()后得到的堆:"; Print(); return t; } return NULL;}bool MinHeap::SwapNode(int i,int j){ swap(heap[i],heap[j]); return true;} |
Huffman类:
#include "MinHeap.h"#ifndef _HUFFMANTREE_H_#define _HUFFMANTREE_H_class Huffman{ MinHeap * mh; //堆,协助建立Huffman树 HuffmanNode * root; //Huffman树的根节点public: Huffman():root(NULL){}; ~Huffman() { delete mh; MakeEmpty(root); } void MakeEmpty(HuffmanNode * ptr) { if(ptr->left) MakeEmpty(ptr->left); if(ptr->right) MakeEmpty(ptr->right); delete ptr; } void CreateHuffmanTree(int arr[],int size); void Print();};#endif#include <iostream>using namespace std;#include <assert.h>#include "HuffmanTree.h"#include "MinHeap.h"#include <queue>void Huffman::CreateHuffmanTree(int arr[],int size){ mh = new MinHeap(size); mh->CreateMinHeap(arr,size); //将数据建立最小堆 int i; HuffmanNode * left; HuffmanNode * right; HuffmanNode * parent; for(i=0; i<size-1; i++) { left = mh->GetMinNode(); //较小成为左孩子 right = mh->GetMinNode(); //较大成为右孩子 //这里可以归结出一个函数来,但是有点麻烦,直观点 parent = new HuffmanNode(left->GetData()+right->GetData()); parent->left = left; parent->right = right; left->parent = right->parent = parent; if(!mh->Insert(parent)) abort(); cout<< "插入父节点之后的堆:"; mh->Print(); } root = parent;}void Huffman::Print(){ queue<HuffmanNode *> q; q.push(root); HuffmanNode * p; while(!q.empty()) { p = q.front(); cout << p->GetData() << " "; if(p->left != NULL) q.push(p->left); if(p->right != NULL) q.push(p->right); q.pop(); }} |
Huffman(哈弗曼,赫夫曼)在通信领域用途很大,在文件压缩技术也有所运用,做些笔记,以后有用,与大家共享,欢迎讨论:)。
当前标签: 别说我学过C++
C++对析构函数的误解 捣乱小子 2011-12-09 11:56 阅读:18 评论:0
C++虚函数和纯虚函数(2) 捣乱小子 2011-12-04 16:16 阅读:62 评论:0
C++虚函数和纯虚函数(1) 捣乱小子 2011-12-04 13:16 阅读:1062 评论:3
C++静态数据成员和静态成员函数 捣乱小子 2011-12-03 13:35 阅读:16 评论:0
sizeof运算符和strlen函数的区别 捣乱小子 2011-11-10 22:53 阅读:15 评论:0



 浙公网安备 33010602011771号
浙公网安备 33010602011771号