2021-OO-第一单元总结

2021-OO-第一单元总结

三次作业的思路

第一次作业

  • 剔除空格无需付出任何犯错误的成本

  • 求导仅涉及简单的幂函数形式

  • 可以根据幂函数次幂数相同便可进行合并化简的细节，以项的幂次为键，该幂次的项的系数作为键值，使用HashMap数据结构进行对应式化简合并。

设计

  • 由于第一次作业表达式形式化描述较为简单，且不用考虑格式检查。

  • 在输入确保正确格式的情况下

    • 表达式中仅为项的加减

    • 项中仅为单个或以乘号相连的因子 

    •  

  • 不难看出，分隔每个项的标志为且仅为有效的加减符号。

  • 有效的加减符号：剔除空白项有数字或者x的加减符号

  • 我们的思路便是将有效的项分隔开来，然后对项进行解析，获取项的信息后进行求导、合并。

  • 思路较为面向过程，便只设计了​Poly类、PolyHandler​类、​RegConstant类三个类，分别用来管理数据、管理处理函数、管理正则常量。

具体实现

输入预处理

  • 剔除空白项

  • 将有效的减符号转化成​+-的形式，以便后面进行分割。

截取有效项

  • 上面提到，分割项的标志是有效的加减符号，经过预处理，我们能够保证有效的加号一定是项与项之间的分隔符。

  • 于是我们根据该符号对表达式进行分割，得到一个String数组Terms

解析项内容

  • 在​HashMao<Exp, Coe>中储存解析结果。

  • 项解析分为以下几步

  • 首先检查项中是否有变量因子​存在

    • 如果有，则进入下一步。

    • 否则，必然为常数项，求导结果为0，略。

    • 解析项的指数

      • 检查并捕获匹配形如*x**4, x**4等进indexFunc数组。

      • 将该数组传进指数处理函数进行处理，解析出指数部分合并后的数值，返回上一层函数并存在临时变量中。

    • 解析项的系数

      • 通过正则将上述的形如​**3的纯指数部分替换为空格，并将剩余的​都替换为空格。

      • 再以空格为分隔符进行split，就可以得到 数字、±x​、空格的组合。

      • 经过条件格式限制，便可以正确解析出项的常系数，返回上一层函数，并存在临时变量中

  • 将得到的指数与系数存放在HashMao<Exp, Coe>​中，待解析完所有项后，通过构造函数得到一个解析完毕的​类。

求导合并

  • 由于本次作业使用了较为偷鸡的办法，所以根据多项式求导的特点，使用HashMao<Exp, Coe>​“一个萝卜一个坑”的特点，进行天生的化简。

  • 遍历​Poly的HashMap​

  • 如果Exp != 0​

    • 如果​HashMap中，包含这个Exp值

      • 将键值对​ 放入新的​中

    • 否则

      • 将键值对​放入新的HashMap​中

  • 在​Poly中放入​flag属性，用来记录其中​是否为空。

  • 忽略x**2的化简是​可以搞成x*x​

输出

  • 因为最终结果的HashMap​是有明确对应关系以及化简结果的，进行分类输出即可。

  • 分类

    • 0

      • 常数串

      • 合并后系数为0

    • x

      • 系数为1，指数为1

    • -x

      • 系数为-1，指数为1

    • m*x

      • 系数为m，指数为1

    • x**n

      • 系数为1，指数为n

    • m*x**n

      • 系数不为[01]，指数不为[01]

总体感受

  • 第一次还没有什么面向对象的思想，加上题目又很像大一程序设计那种输入->处理->输出结果的过程题，于是本人就写了一堆函数来处理数据、输出数据，虽然做起来很容易，但是容易出错且难以解决。

第二次作业

设计

  • 由于第一次的设计过于不可持续，没有考虑很多未来的需求，比如第一次的分隔符切割出项的方法对于多层嵌套的数据毫无还手之力，于是这次不得不进行重构。

  • 为了应对递归的需求，本次决定通过递归下降的方法进行处理。

  • 主要类为​三个类，​Factor类中包含不同的因子类​来进行统一的管理

  •  

     

  • 配置了一个静态方法类MyUtils​作为工具包，完成一些所有类中都可以通用的静态方法。（后来发现可以用接口实现统一化的管理）

  • 个人的思路就是使用递归下降去破解多层嵌套以及未来可能出现的格式检查。但是实现方式过于暴力，采用了自动机的方式，设置了两个静态变量Main.index, Main.expr，​和​来保证递归解析表达式时，在所有递归函数中都可用。

  • 解析完表达式后，分别在Expr​中获得​Term的集合、Term​中获得Factor​的集合。

  • 求导时，对原表达式进行求导，表达式会调用下层Term的​求导，​Term会根据求导法则对每个Factor​进行求导。

  • ​Expr求导返回的是​Term的集合，​Term求导返回的也是Term​的集合，​Factor求导返回的是Factor​的集合。

  • 构造出相应情况的toString()​方法，输出时对Expr​调用该方法，逐级调用下层类的该方法以获得完整的输出。

实现

  • 根据形式化表达进行逐步实现

  • 实现其实比较boring，当时其实别无选择，只能完全重构写递归下降，迫于生存的本能（bushi，选择了C语言写法的递归下降。。。

  • 具体就是类似有限自动机那种逐字符判断每个输入是否合理，并解析获得每个因子的属性，在此不再赘述。

  • ​

  • 由于时间紧迫没有采用任何优化，求导根据最暴力的组合求导法则进行完全展开。。。

感受

  • 由于没有进行优化，且递归写的不是很熟练，导致出现了不必要的多次递归（tle），而且性能分惨不忍睹，每次求导都完全展开不合并同类项真的是人干出来的事情吗（？）

  • 感觉还是没设计好.jpg

第三次作业

设计

  • 整体架构同第二次，只不过增加了格式检查异常以及对Factor类进行了统一化的处理，将三角因子、幂函数因子、常数因子、表达式因子只保留特性部分，而去掉多余的部分。

    • 例如三角函数前的系数等，严格按照形式化描述，分为 常数因子​ 三角因子。

      • 因此对求导部分进行改变，因子求导返回的是因子的集合，可能包含所有子因子，如对三角函数求导可能返回两种三角因子以及常数因子组成的集合（在生成因子集合时也应该进行合并同类项）。

      • 这样就完成了因子的单纯化，在第二次作业中因子包含系数是一个很冗余的事情。

  • 由于上一次性能分过低，这次采用合并同类项的基本优化方法进行优化，在每次将元素放入集合​时，都会查找是否有equals相同的元素，如果有，则进行对应的merge处理，这样就保证了集合中的项始终处于最简状态。

  • 最简状态：无法再找到除了涉及括号合并同类项的最简式。

实现

  • 与第二次相比的迭代之处就在于为化简做出的努力。

    • 为了合并同类项覆写了无数个​和​

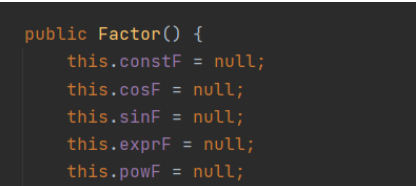
    • 由于一直没开窍使用接口和继承，我选择在Factor中内置五个因子的引用对象属性。。。。。

      • 想法很简单，这样比较粗暴，初始时都给每个因子赋null值，在程序设计时确保每个factor只有一个引用属性不为空。。。。（下次不敢这样了.jpg）

      • 带来了很多的问题，比如要操作因子就需要使用大量的控制分支语句进行管理

      •  

         

         

感受

  • 首先是不重构的快乐，第二次重构写的人都没了。

程序结构分析

复杂度分析

  • 量化分析主要参考基本复杂度​、模块设计复杂度 、​圈复杂度这几个定义，具体的含义可以自行百度。但是总的来说，他们总体符合数值越大，程序可读性、稳定性、可维护性越差的趋势。

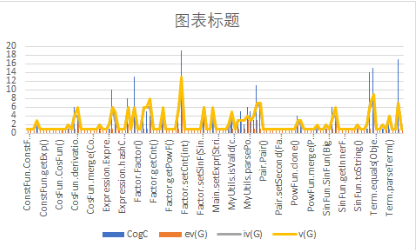
  • 以下是通过可视化的方式观察几次作业中复杂度的变化。

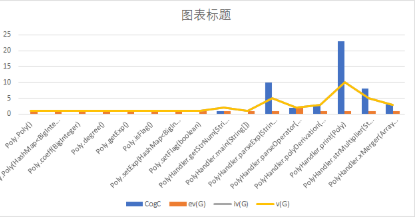
    • 第一次作业

      •  

         

      • 可以看出，在第一次作业采取的面向过程的编程方法指导下，相较于后两次作业而言程序类的个数较少，总的复杂度数也较小，但是不难看出认知复杂度还是集中在打印输出函数中，一定程度上反应该函数不好理解，也不出所料，在这个函数中强测被hack了一个点。由此可见程序复杂度和出错的概率还是有相当大关系的。

    • 第二次作业

      •  

         

      • 第二次作业是经过重构得到的，完全废弃了之前不可持续的思路。

      • 可以看出，重构后圈复杂度总数提高了很多，这里面主要是因为重构之后为了应对递归的情形，设置了大量的控制分支完成递归下降，但圈复杂度并不能代表一切。从平均较低的​我们不难看出，代码的可重构性和理解难易度还是较之前有了较大改观，各种复杂度的峰值有了明显的下降，分布也明显的更加平均。

      • 因此，从复杂度角度看，面向对象的数据管理和方法管理能够显著降低复杂度，提高程序可读性。

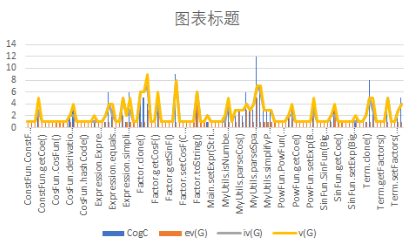
    • 第三次作业

      •  

         

      • 相较于第二次作业，第三次作业的平均复杂度进一步降低。

      • 首先是因为对于因子的划分更加清晰（将他们分为互不相关的原子因子），其次，在第三次作业加入了合并同类项的众多shit山代码后，复杂度居然没有爆炸式的增长，归功于高可重构性，让我只是覆写了很多hashcode（），而没有加特别特别多的ifelse，因为之前加过了（悲）。

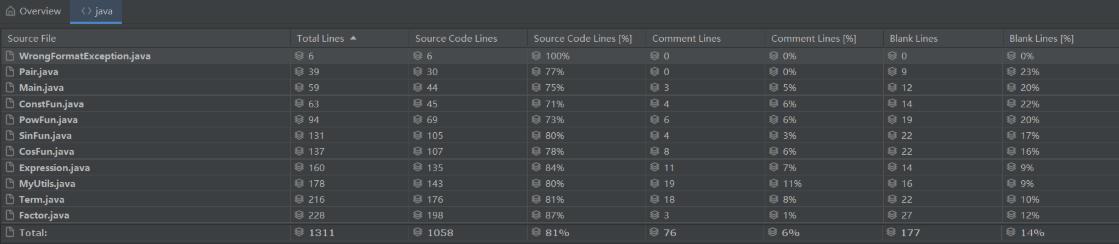
代码长度分析

  • 第一次作业

    •  

       

    • 作为一个函数式的程序，纯面向过程的行数一定是较少的，没有过多评价（留下重构蒟蒻悲伤的泪水）。

  • 第二次作业

    •  

       

    • emm 第二次作业有点挣扎的感觉，写的时候缺乏考虑，且工程量偏大。

    • 主要是因为完全重构以后，新的架构较为清晰但不够鲁棒，因子与因子间没有达到原子正交化，会有很多bug，且码量集中在每个类中的固定的、、、​等标准配套方法，我都用了idea的自动生成，一天还是只写了六七百行，这是十分累人的。（ps：其实可以加几个接口进行统一管理的）

    • 吃一堑长一智，提前设计好再开始写。

  • 第三次作业

    •  

       

    • 在第二次作业基础上进行迭代开发。

    • 增加的代码主要集中在合并同类项和求导操作中， 整体大框架没有动， 迭代yyds！

    • 但要注意Factor、Term类的代码量还是超过了200行，其实是存在更好的解决办法的。（使用继承、多态、接口）

    • 比较无语的是Term和Expression类里还存在着没删掉的待开发代码。。（下次一定

  • 总的来看，一句话，架构设计好迭代开发压力真的会小很多。

内聚与耦合分析

  • 内聚和耦合通俗说就是在描述程序之间的联系程度。函数与函数之间、类与类之间联系程度高，叫做高耦合；反之就叫高内聚。

  • 内聚和耦合从来不是必然的贬义词或褒义词。必要的耦合是不可避免的，如这次作业的递归下降做法。但我们可以尽力追求合理情况下，较低的耦合程度，来保证程序的优美和简洁。

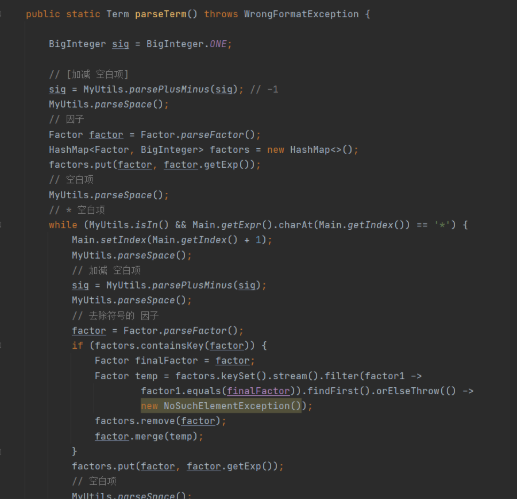
  • 递归下降方法中，所有解析函数和求导函数其实都是层层嵌套、互相耦合的。

  • 如 

     

     

  • 我们要做的可能就是在一些不合理的地方尽量解耦。

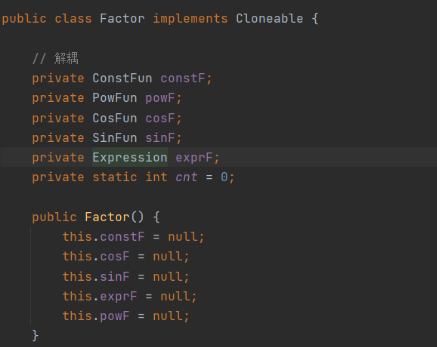
    • 比如自己的Factor类懒省事，为了表达、调用不同因子，就把所有因子类的实例塞进了Factor类

      •  

         

      • 这样其实是很反人类的，血压一下子就高起来了（

      • 明明可以写成一个抽象类 + 五个继承来的子类， 可以让这个长达210+行的大类被拆解。

  • 解决方法

    • 尽可能多的使用接口、继承等java特性

    • 类属性中放多个引用对象时，及时反思

    • 看到较不合理的程序行数时，分析下为啥（别一路向西.jpg

类图

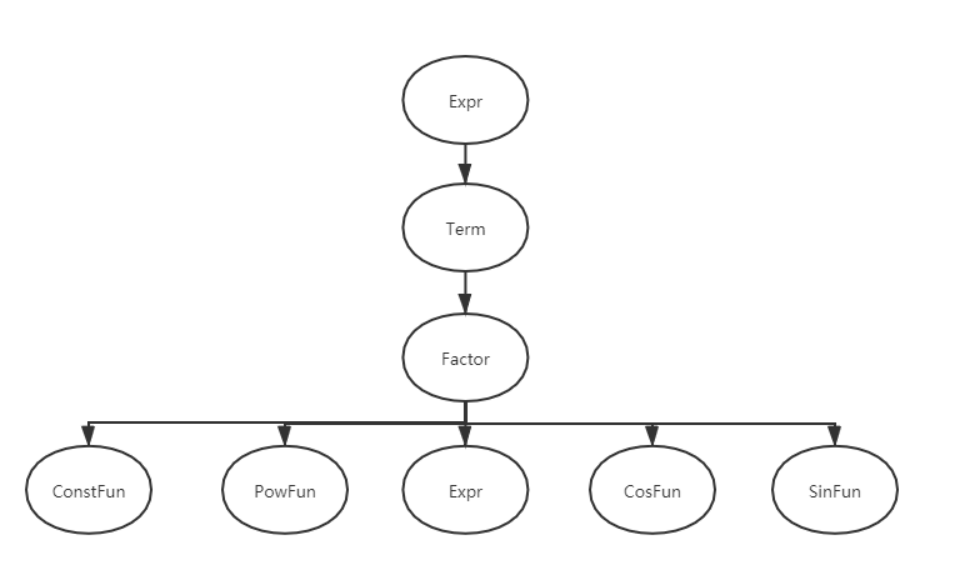
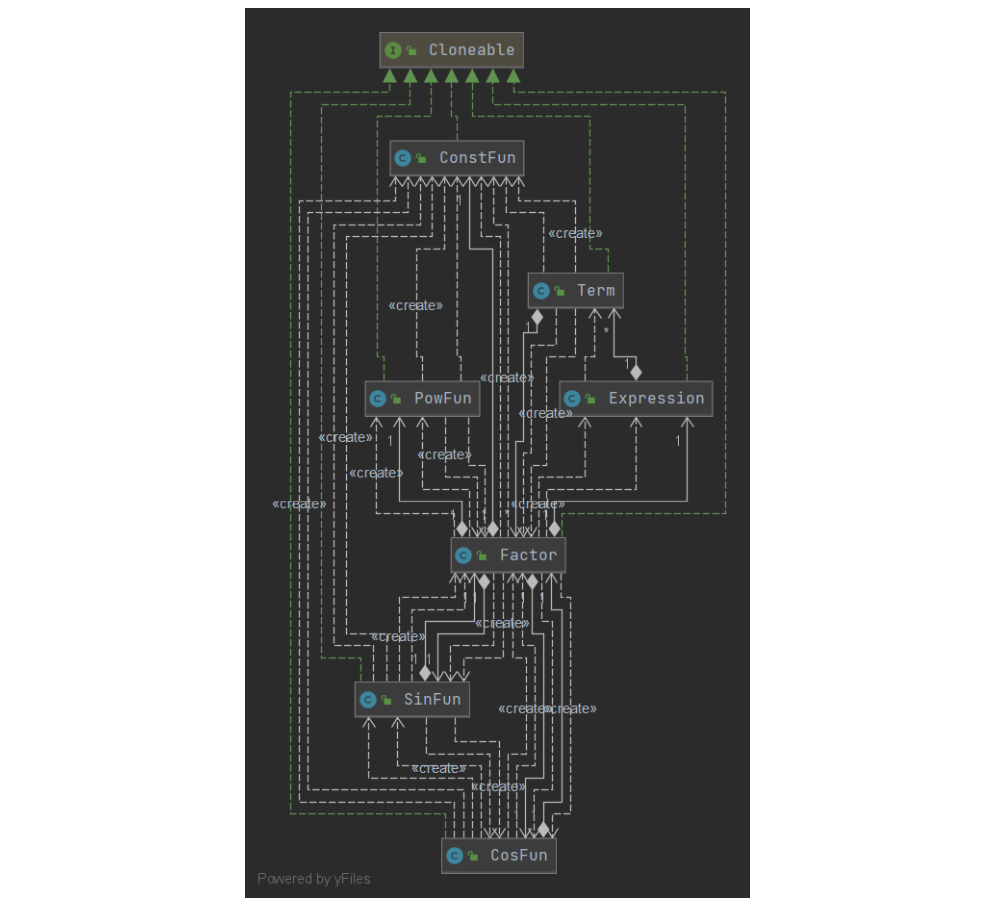
  • 以第三次作业为例分析类图

    •  

       

    • 设计的想法就是从形式化描述出发的。

      • 表达式只由项加减构成

      • 项只由因子相乘得到

      • 因子只有固定的几类

    • 于是有这种 "机制与策略分离" 的设计

      • 表达式->terms属性(机制)->项的集合->其中的项之间属于加减关系(策略)

      • 项->factors属性(机制)->factor之间属于乘除关系(策略）

    • 解析、求导以及最终的输出也是这样一层层逐次调用。

    • 优点是比较清晰，缺点是其实有的地方做的还不是那么好，比如不必要的高度耦合。

程序bug分析

  • bug总数五个

    • 第一次一个

      • 为输出问题手抖了

    • 第二次两个

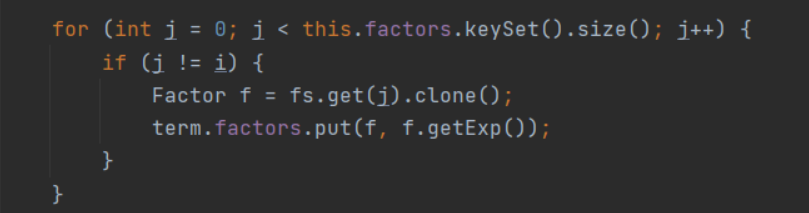
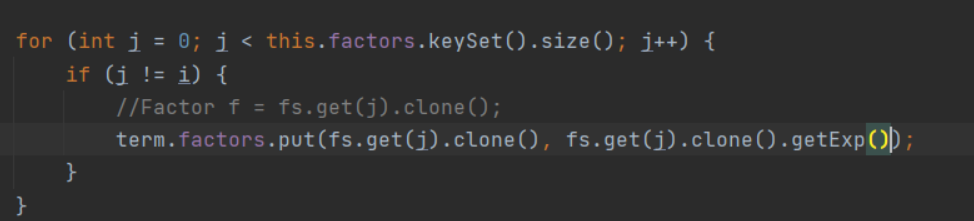
      • 递归调用写次了

        •  

           

        • 这个地方原来的写法是

           

           

        • 直接tle

      • 输入为0时输出空（nt了

    • 第三次两个

      • 一个是sin((x)这种wf没判出来（因为当时对右括号放松了警惕

      • 另一个是求完导后对Term合并同类项时，忘记合并（我以为我合并了系列

  • 出现bug的类从上面的复杂度分析可以看出，都属于认知复杂度和圈复杂度较高的地方。

bug寻找策略

  • 搞错了方向

    • 刚开始确实如纪一鹏老师讲的，为了体验圣杯战争，手动随意构造了几个样例点，完全看运气。

    • 后来得到了多个版本的评测机，就对着别人的代码进行无脑轰炸，后来发现没有意思。

    • 在最后一周索性躺平，去做其他事情。

  • 思考

    • 在最后fixbug的时候，看到房里一个兄弟hack出了自己强测没测出来的bug，而且显然那个样例是很巧妙的很精致的样例。

    • 在最后一周里，多次想和助教、老师反映互测的鸡肋性。后来想想，其实互测的初衷还是互相学习互相测试的过程，和分数无关。老师在总结课上的观点更加支持了我的想法，遂决定在之后的互测中认真学习房内代码思路，不浪费机会，只是向分看。

    • 如果不是目的性特别强的人，其实多去看看别人的代码，少去盯着分数，多想想总是没有坏处的。在学习的过程中过于功利过于趋众还是会害了自己，最后丧失独立思考的能力。

重构经历总结

  • 其实上面该说的都说了，但重要的事情要多说几遍

    • 写代码前要想明白，想清楚。

    • 当自己感觉事情不对的时候，一定要停下来找出来到底是哪里不对。

    • 不要为了使用某种方法而使用某种方法，比如这次hashmap就没啥必要。

    • 重构要趁早，憋到最后自己心态很受影响。

心得体会

  • 总的来说第一单元感觉很失败，无论从得分讲，还是从收获讲。用几次惨痛的经历让自己接下来正确面对自己的OO课程。

  • 字少事大（确信

 

 

 

posted @ 2021-03-26 23:42  WuhuAirforce  阅读(98)  评论(1)    收藏  举报