编译原理（二）

一、文法的形式化定义

（1）G=(，，P，S)

     ：终结符集合，终结符是文法所定义的语言的基本符号，有时也称token，例如：={Apple，boy，eat，little}

     ：非终结符集合，非终结符是用来表示语法成分的符号，有时也称为“语法变量”，例如： ={<句子>,<名词短语>,<动词短语>,····}

    注意： ∩=Φ        ∪ ：文法符号集。

    P：产生式集合，产生式描述了将终结符和非终结符组合成串的方法产生式的一般形式：α→β 读作：α定义为β（或由·····组成）

    α∈(∪ )+，且α中至少包含VN中的一个元素：称为产生式的头(head)或左部(left side)

    β∈(∪ )* ：称为产生式的体(body)或右部(right side)

    S：开始符号，S∈。开始符号表示该文法中最大的语法成分，例如：S=<句子>

（2）产生式的简写：对一组有相同左部的α产生式α→β1 , α→β2 , … , α→βn

    可以简记为：α→β1 | β2 | … | βn

    读作：α定义为β1，或者β2，…，或者βn ，β1，β2，…，βn称为α的候选式(Candidate)

（3）符号的约定

        下述符号是终结符：字母表中排在前面的小写字母，如 a、b、c；运算符，如 +、*等；标点符号，如括号、逗号等；数字0、1、. . . 、9；粗体字符串，如id、if等。

        下述符号是非终结符：字母表中排在前面的大写字母，如A、B、 C；字母S。通常表示开始符号；小写、斜体的名字，如 expr、stmt等；代表程序构造的大写字母。如E(表达式)、T(项)和F(因子)

除非特别说明，第一个产生式的左部就是开始符号。

二、语言的形式化定义

推导：

    给定文法G=(，，P，S)，如果 α→β ∈ P，那么可以将符号串γαδ中的α替换为β，也就是说，将γαδ 重写(rewrite)为γβδ，记作 γαδ => γβδ。此时，称文法中的符号串 γαδ 直接推导(directly derive)出 γβδ，也就是用产生式的右部替换产生式的左部。

例：推导与归约的过程

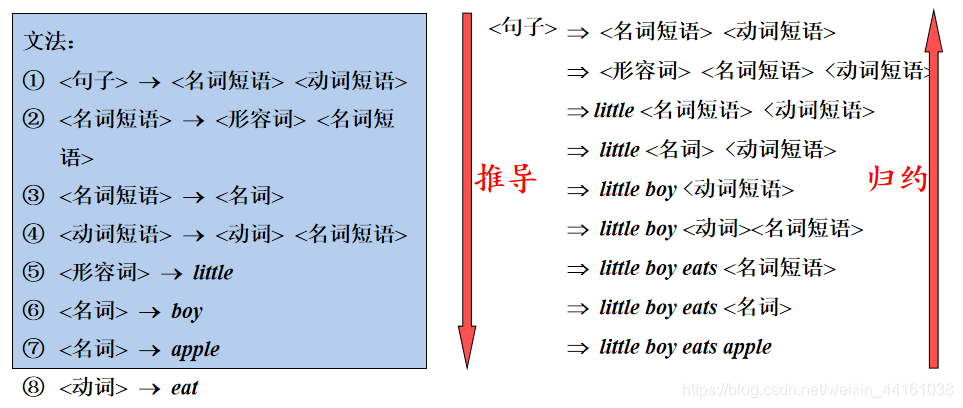
归约：就是用产生式的左部替换产生式右部的过程

句子和句型：

    如果S=>*α，α∈(∪ )*，则称α是G的一个句型。一个句型既可以包含终结符，又可以包含非终结符，也可能是空串

    如果S=>*w,w∈*，则称w是G的一个句子，句子是不包含非终结符的句型

问题：有了文法（语言规则），如何判定某一词串是否是该语言的句子？

解答：一、从生产语言角度，由该文法推导出这一词串

           二、从识别语言角度，由该词串归约出次文法

由文法G开始符号S推导出的所有句子构成的集合称为文法G生成的语言，记为L(G),即L(G)={w|S=>*w,ww∈*}

语言上的运算：

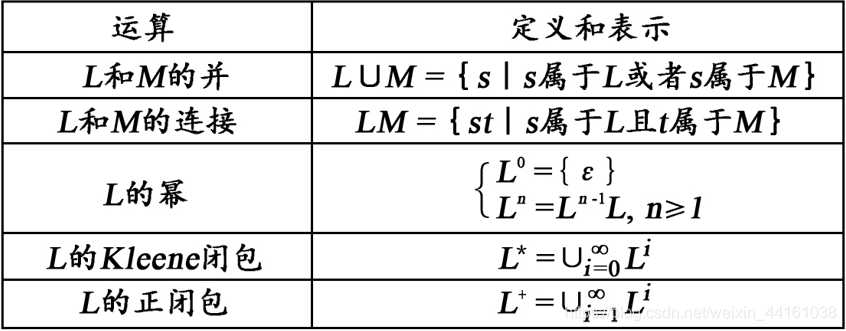
例：令L={A，B，…，Z，a，b，…，z}，D={0，1，…，9}。则L(L∪D)*表示的语言是标识符。

三、文法的分类

乔姆斯基将文法分为四种类型：0型，1型，2型，3型。

1.0型文法 α → β

无限制文法/短语结构文法（PSG）：∀α → β∈P， α中至少包含1个非终结符

0型语言：由0型文法G生成的语言L(G)

2.1型文法 α → β

上下文有关文法（CSG）：在0型文法的基础上，∀α → β∈P，｜α｜≤｜β｜  ，产生式的一般形式： α1Aα2 → α1βα2 ( β≠ε ) ，不包含ε-产生式

上下文有关语言（1型语言）：由上下文有关文法（1型文法）G生成的语言L(G)。

3.2型文法 α → β

上下文无关文法（CFG）：在1型文法的基础上，∀α → β∈P，α ∈ ，产生式的一般形式：A→β

上下文无关语言（2型语言）：由上下文无关文法（2型文法）G生成的语言L(G)。

4.3型文法 α → β

正则文法（RG）：右线性(Right Linear)文法： A→wB 或 A→w

                                左线性(Left Linear)  文法： A→Bw 或 A→w

正则语言（3型语言）：由正则文法（3型文法）G生成的语言L(G)，正则文法能描述程序设计语言的多数单词。

5.四种文法之间的关系

逐级限制：

• 0型文法：α中至少包含1个非终结符
• 1型文法（CSG） ：｜α｜≤｜β｜
• 2型文法（CFG） ：α ∈
• 3型文法（RG）：A→wB 或 A→w   (A→Bw 或A→w)

逐级包含

四、CFG（上下文无关文法）的分析树

1.CFG分析树

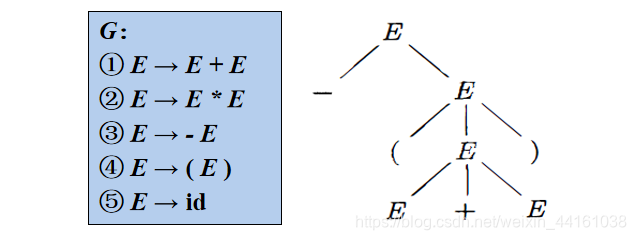
根节点的标号为文法开始符号 ；

    内部结点表示对一个产生式A→β的应用，该结点的标号是此产生式左部A 。该结点的子结点的标号从左到右构成了产生式的右部β；

    叶结点的标号既可以是非终结符，也可以是终结符。从左到右排列叶节点得到的符号串称为是这棵树的产出( yield )或边缘(f rontier) 。

2.分析树是推导的图形化表示

给定一个推导 S => => =>…=>  ，对于推导过程中得到的每一个句型，都可以构造出一个边缘为的分析树

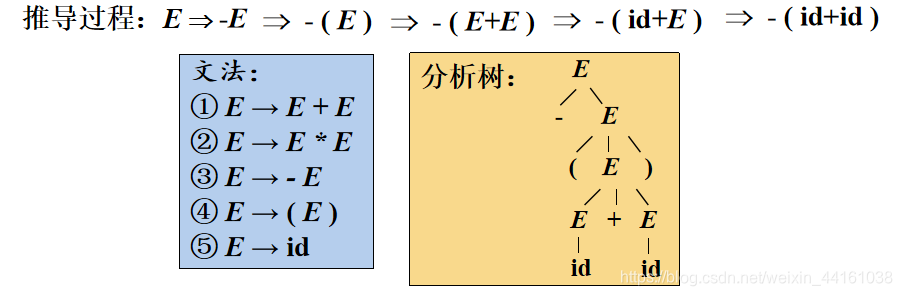
3.(句型的)短语

        给定一个句型，其分析树中的每一棵子树的边缘称为该句型的一个短语(phrase) ，如果子树只有父子两代结点，那么这棵子树的边缘称为该句型的一个直接短语(immediate phrase) 

4.二义性文法

        如果一个文法可以为某个句子生成多棵分析树，则称这个文法是二义性的。

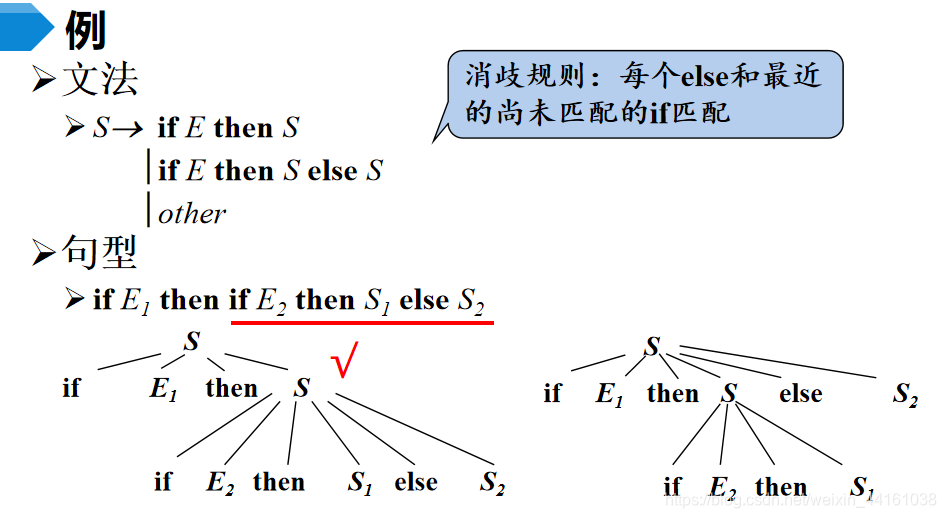
 二义性文法的判定：对于任意一个上下文无关文法，不存在一个算法，判定它是无二义性的；但是能给出一组充分条件，满足这组充分条件的文法是无二义性的，满足肯定是无二义性，不满足也未必就有二义性。