关于码字距离的一些猜想

瞎猜一下，为什么码据为1的时候没有检错能力，码据为2的时候有检错能力，码据大于等于3的时候有纠错能力
看到个词：线性码，作为一个不会任何通信原理的人，我不负责任的瞎猜一下。
把码字所有的位数n的所有状态，按照某种方式和数轴上的整数一一对应。我们这里方便起见，就按照从小到大把。码字代表的状态用蓝色下表。

我这里就很偷懒了。我直接用数轴上的距离来处理。n=1的时候，落不到错误状态，没办法检错。n=2的时候，至少可以对一个状态而言，它可以是码字，也可以不是，二分了。所以只有检错能力。但是n=3的时候，就出现了距离这个概念。我这里有一个想法，这个距离“码字”的距离也是一种状态。状态越是靠近某个码字，那么就越有可能是那个码字——也许继续是概率论？我这个距离和几何表示方法很简陋，也很直白，我是相信一定有更好的已经被研究而且应用了。比如码据而不是我这里的线性距离，又或者不是单纯的一位表示，而是更高维度的表示方法，比如n=2是一个二维坐标系，n=3的时候是三维坐标系？n趋于无穷岂不是一个无穷维度的（笑）
继续有个想法。
维度拓展？比如从n=1开始，我们规定x轴，就有0，1，算了直接画图吧。

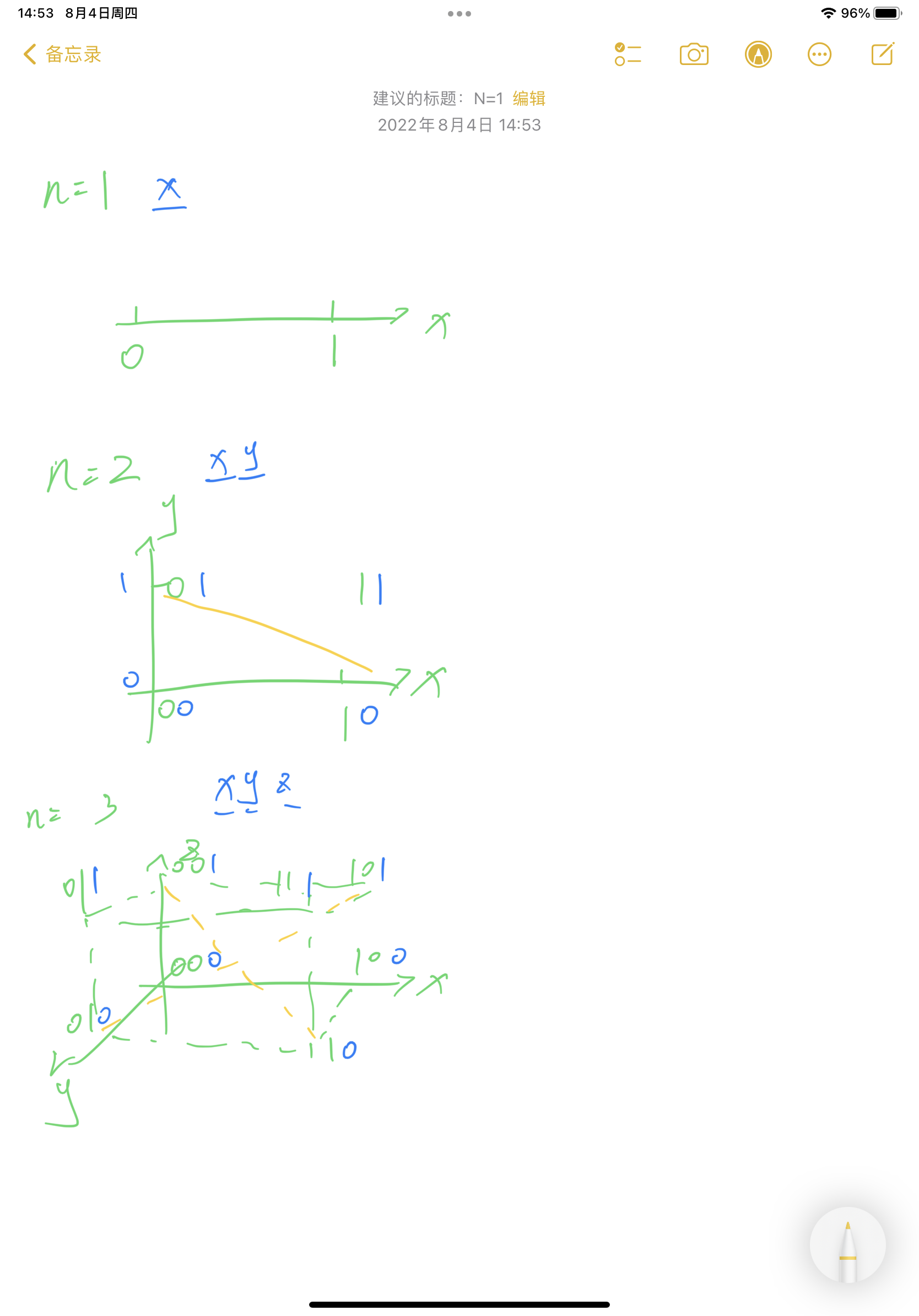
这似乎也是一种设计方法，尽可能地拉开且均分每个码字的距离。但是几何方法似乎只能到3维，更高维就只能上代数方法了。反正我做不到。我是菜鸡。这玩意怕不是早就写在某些课本上了。瞎猜也是好的。
继续复习408了，我要上深大呜呜呜我好菜