GDCPC广东省赛F-Fake Math Problem题解

GDCPC广东省赛F-Fake Math Problem题解

原题链接

前言：

赛场上一开始没发现naughty的998241383不是质数，一直想着逆元推式子，后来发现不是质数后就不太有思路了，比赛结束发现朋友们是用线段树做的，今天复盘想出了较为“数学”的解法（好像也是官方题解）

思路：
998241383=673×937×1583，而

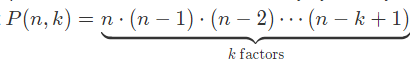
我们发现，外层循环枚举n，内层循环枚举a[i],内层循环的次数不会太大，因为当内层k枚举超过1583时，P(i, k)为连续1583个数相乘，其中必有673,937,1583的倍数，他们相乘后mod淘气数则为0，所以内层循环至多1583次，直接枚举就好，内层判断一下P值是否为0，为0则break，时间复杂度O(1583n)
代码如下：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod = 998241383;
ll t;
ll a[100010];
ll n;
ll P;
ll ans;
int main() {
    ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
    cin >> t;
    while (t--) {
        cin >> n;
        for (int i = 0; i <= n; i++) {
            cin >> a[i];
        }
        ans = 0;
        for (int i = 0; i <= n; i++) {
            P = 1;                                  //初始化P值为1
            for (int j = 0; j <= a[i]; j++) {
                ans = (ans + P) % mod;
                P = (P * (i - j)) % mod;        //乘上下一个相邻的数
                if (P == 0) break;                //如果为0则退出循环
            }
        }
        cout << ans << "\n";
    }
    return 0;
}

反思

面向模数解题法，学到了学到了Qwq

​