归并排序

【分】

【治】

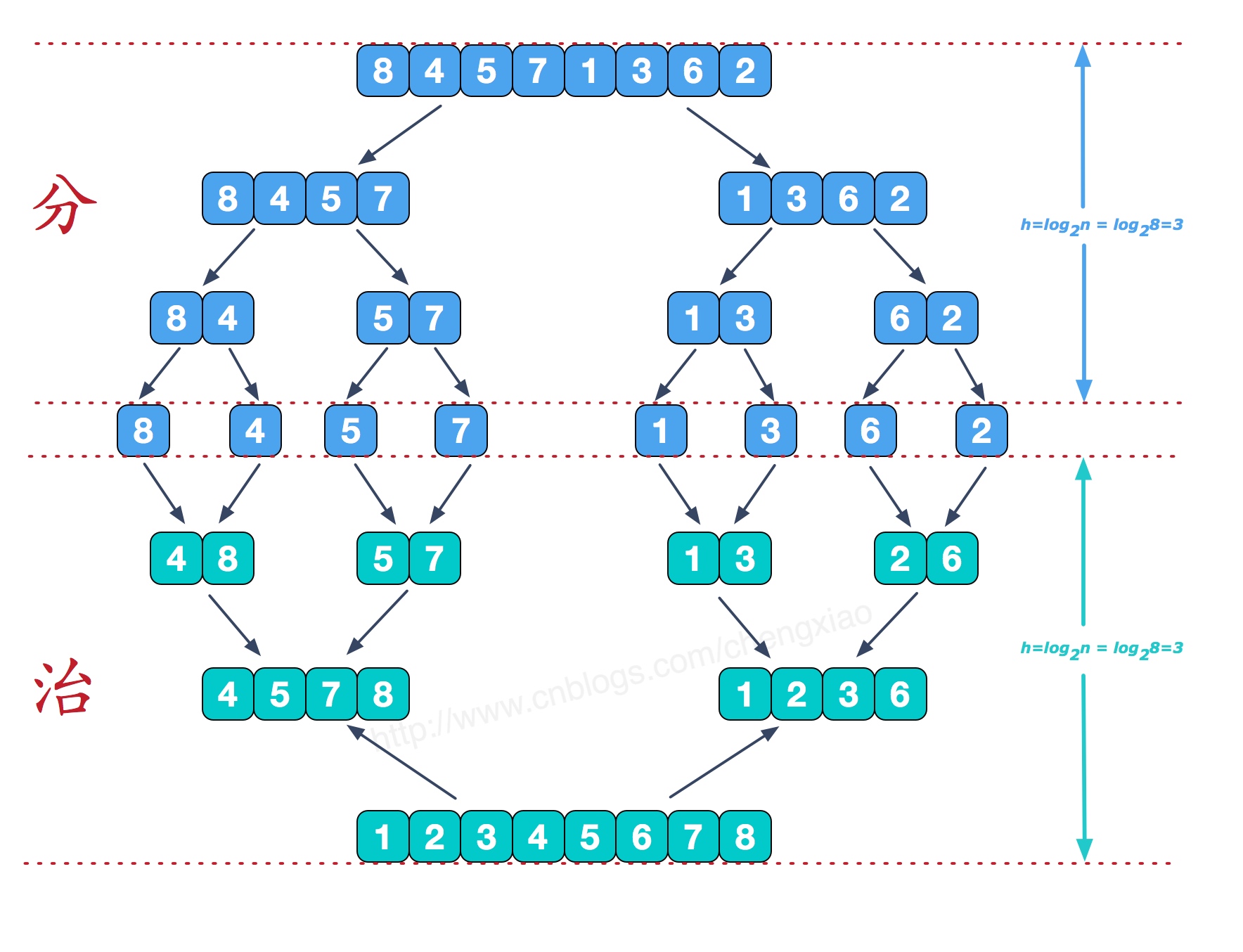
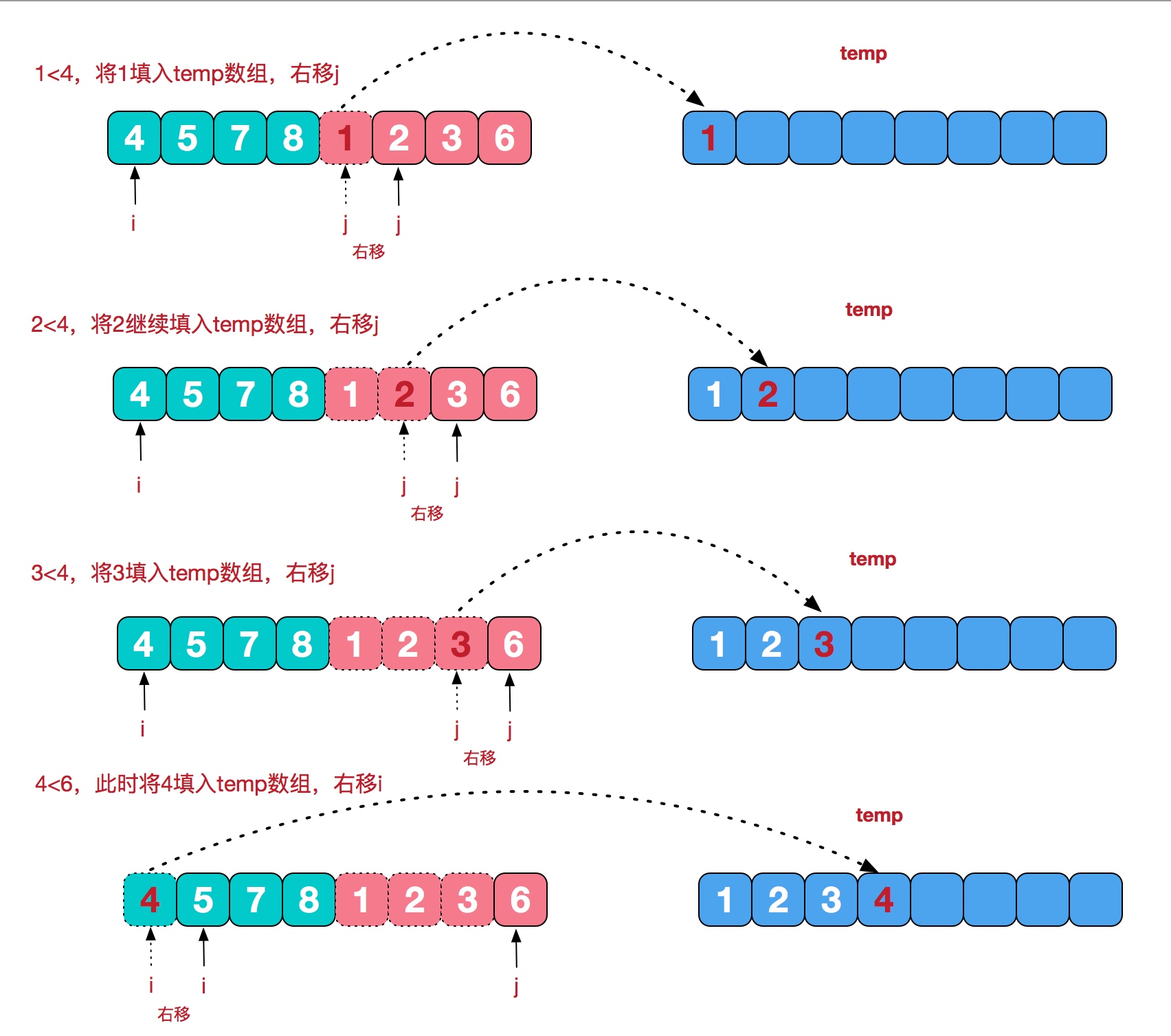
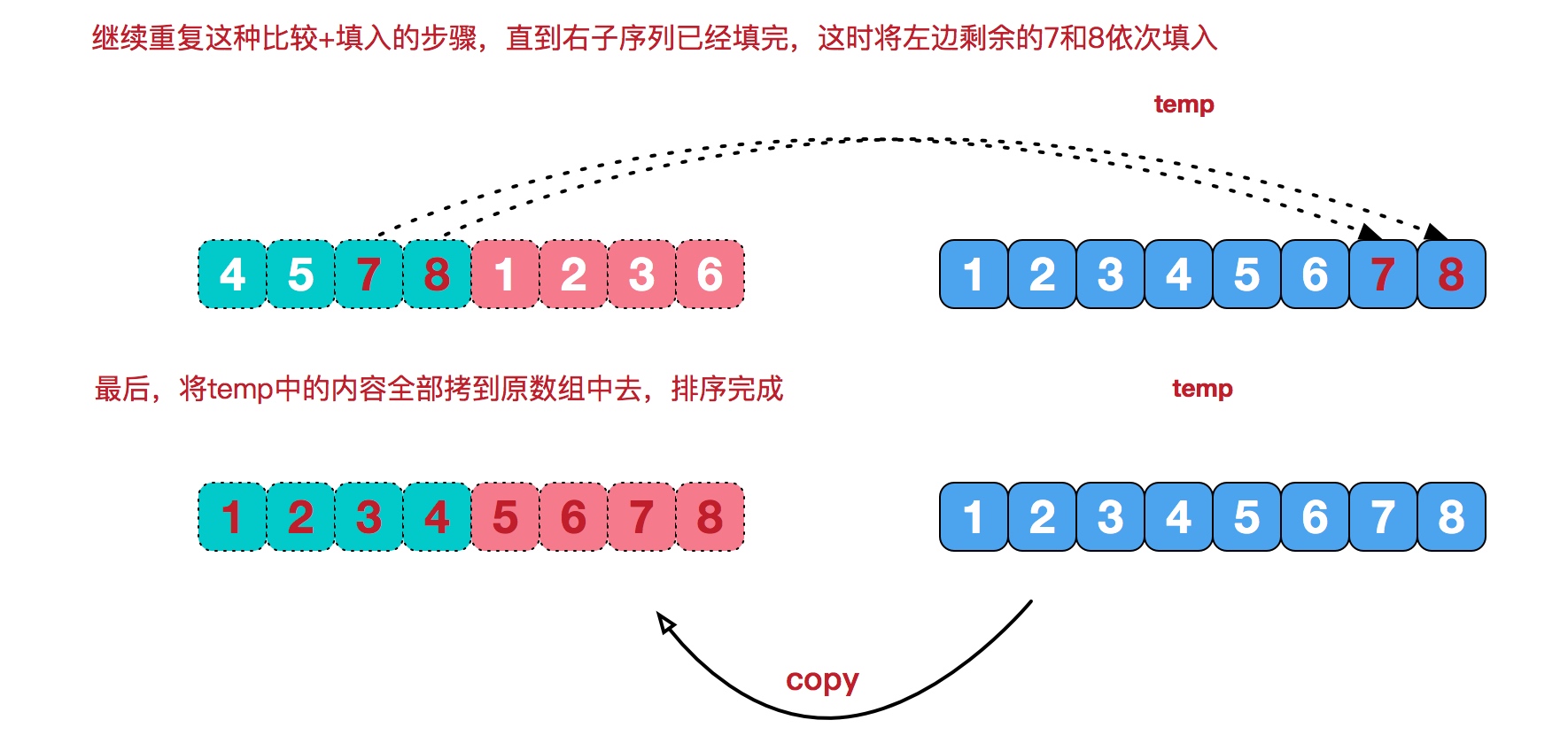
归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

递归，就是在运行的过程中调用自己。
构成递归需具备的条件：

1. 子问题须与原始问题为同样的事，且更为简单；
2. 不能无限制地调用本身，须有个出口，化简为非递归状况处理。

package com.example.leetcode.easy;

import org.slf4j.Logger;
import org.slf4j.LoggerFactory;

import java.util.Arrays;

/**
 * @author LiPeng01
 * @since 2021/2/27 10:38 上午
 */
public class Merge {
    public static void main(String[] args) {
        int[] num ={9,8,7,6,5,4,3,2,1};
        sort(num);
        Logger logger = LoggerFactory.getLogger(Merge.class);
        logger.info(Arrays.toString(num));
    }
    public static void sort(int[] nums) {
        //在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        int[] tmp = new int[nums.length];
        divideAndSort(nums, 0, nums.length-1, tmp);
    }

    /**
     * 函数作用,将指定数组nums分而治之,得到一个[left,right]排序后的数组
     * @param nums
     * @param left
     * @param right
     * @param tmp
     */
    public static void divideAndSort(int[] nums, int left, int right, int[] tmp) {
        //什么时候left>=right呢
        // 1. 当待分割数组长度仅为1的时候,分割后,数组mid = (left+right)/2; mid == left ;mid == right; mid+1 > right;
        // 2. 当待分割数组长度仅为2的时候,分割后,数组mid = (left+right)/2; mid == left ; mid+1 == right ;
        if(left<right) {
            int mid = (left+right) /2 ;
            //分割左半边数组,并对左半边数组排序.左边归并排序，使得左子序列有序
            divideAndSort(nums,left,mid, tmp);
            //分割右半边数组,并对右半边数组排序.右边归并排序，使得右子序列有序
            divideAndSort(nums,mid+1, right,tmp);
            //合并左右数组,将两个有序子数组合并操作
            merge(nums,left,mid,right,tmp);
        }
    }

    /**
     * 合并数组,将左右半边数组按顺序合并
     * @param nums
     * @param left
     * @param mid
     * @param right
     * @param tmp
     */
    private static void merge(int[] nums, int left, int mid, int right, int[] tmp) {
        //左序列指针
        int i = left;
        //右序列指针
        int j = mid+1;
        //临时数组指针
        int k = 0;
        //如果两个数组都没到边界,则将其填充进临时数组
        while (i<= mid && j<=right) {
            //谁小谁填充,并移动指针
            if(nums[i] <= nums[j]) {
                tmp[k++] = nums[i++];

            }else {
                tmp[k++] = nums[j++];

            }
        }

        //如果是左序列没有填充完,则将剩下的元素都填充到临时数组末尾
        while (i<=mid) {
            tmp[k++] = nums[i++];

        }
        //如果是右序列没有填充完,则将剩下的元素都填充到临时数组末尾
        while (j<=right) {
            tmp[k++] = nums[j++];

        }

        //重置临时数组指针
        k = 0;
        //将排序好的所有元素,从临时数组复制到原数组上,此时原数组[left,right]有序
        while (left <= right) {
            nums[left++] = tmp[k++];
        }
    }


}