TensorFlow+实战Google深度学习框架学习笔记（10）-----神经网络几种优化方法

神经网络的优化方法：

1、学习率的设置（指数衰减）

2、过拟合问题（Dropout）

3、滑动平均模型（参数更新，使模型在测试数据上更鲁棒）

4、批标准化（解决网络层数加深而产生的问题---如梯度弥散，爆炸等）

 

一、学习率的设置----指数衰减方法

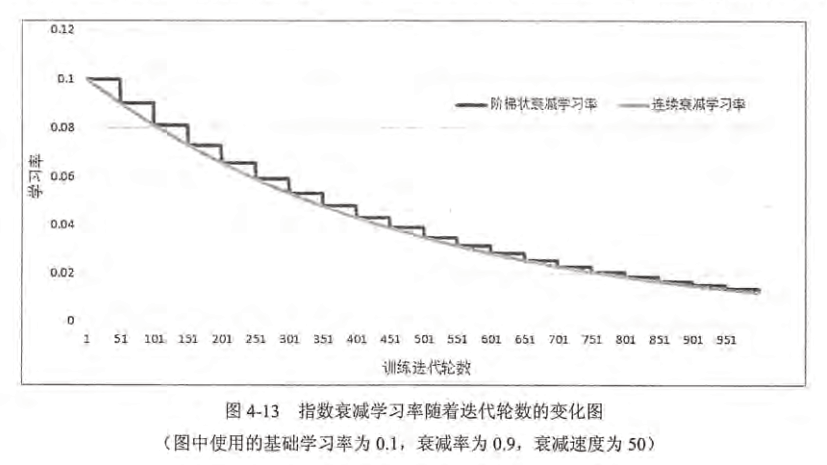
通过指数衰减的方法设置GD的学习率。该方法可让模型在训练的前期快速接近较优解，又可保证模型在训练后期不会有太大的波动，从而更加接近局部最优。

学习率不能过大，可能让参数在极值两侧波动，不能过小，训练时间会过长。

TensorFlow提供的方法：tf.train.exponential_decay函数实现了指数衰减学习率。通过这个函数，可以先使用较大的学习率来快速得到一个比较优的解，然后随着迭代的继续逐步减小学习率，使得模型在训练后期更加稳定。exponential_decay函数会指数级地减少学习率：

 

 应用：

 

 二、过拟合问题：

过拟合：一个模型过于复杂时，只记得去学习训练数据中随机噪声而忘了去学习训练数据中通用的趋势。

避免过拟合的方法：正则化、数据增强（增加训练数据）、提早终止训练、参数共享、批标准化、集成方法、辅助分类节点

正则化：在损失函数中加入刻画模型复杂程度的指标。通过限制权重的大小，得到模型不能拟合训练数据中的随机噪音。

TensorFlow中的L2正则化的损失函数定义：

提高代码可读性：可以运用集合collection的思想，即将均方误差损失函数和正则化损失函数分开计算，然后放入loss【自己取名】的集合中，最终再从集合中取出求和。

三、滑动平均模型【参数的更新】

作用：

使用滑动平均模型在很多应用中都可以在一定程度提高模型在测试数据上的鲁棒性。

其实滑动平均模型，主要是通过控制衰减率来控制参数更新前后之间的差距，从而达到减缓参数的变化值（如，参数更新前是5，更新后的值是4，通过滑动平均模型之后，参数的值会在4到5之间）

如：本次结果=(1-a)本次采样值+a上次结果

目的：平滑、滤波，即使数据平滑变化，通过调整参数来调整变化的稳定性。

为何在测试阶段使用：

对神经网络边的权重 weights 使用滑动平均，得到对应的影子变量 shadow_weights。在训练过程仍然使用原来不带滑动平均的权重 weights，不然无法得到 weights 下一步更新的值，又怎么求下一步 weights 的影子变量 shadow_weights。之后在测试过程中使用 shadow_weights 来代替 weights 作为神经网络边的权重，这样在测试数据上效果更好。因为 shadow_weights 的更新更加平滑，对于随机梯度下降而言，更平滑的更新说明不会偏离最优点很远；对于梯度下降 batch gradient decent，我感觉影子变量作用不大，因为梯度下降的方向已经是最优的了，loss 一定减小；对于 mini-batch gradient decent，可以尝试滑动平均，毕竟 mini-batch gradient decent 对参数的更新也存在抖动。

比如：在最后的1000次训练过程中，模型早已经训练完成，正处于抖动阶段，而滑动平均相当于将最后的1000次抖动进行了平均，这样得到的权重会更加robust。

应用：

tensorflow提供了tf.train.ExponentialMovingAverage（decay, num_updates=None, name='ExponentialMovingAverage'）这个接口。

  • decay：一般设置为非常接近1的数，比如0.9999，
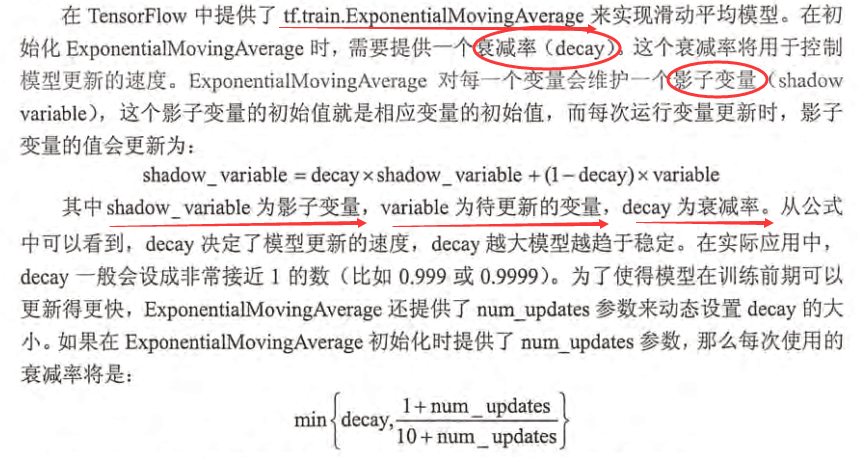
  • num_updates：为了在初期快速的更新，可以设置num_updates，如果num_updates = None ,那么decay将为一个固定的值。设置num_updates=global_step，那么dacay将会根据如下公式选择decay值：

                    min(decay, (1 + num_updates) / (10 + num_updates))

使用MovingAverage的三个要素。

  1. 指定decay参数创建实例： 
    • ema = tf.train.ExponentialMovingAverage(decay=0.9999)
  2. 对模型变量使用apply方法：
    • maintain_averages_op = ema.apply([var0, var1])
  3. 在优化方法使用梯度更新模型参数后执行MovingAverage：
    • with tf.control_dependencies([opt_op]):
          training_op = tf.group(maintain_averages_op)
      其中，tf.group将传入的操作捆绑成一个操作。

以下的代码有以下几点要注意：

1） 定义好ema之后，分两步，一步ema.apply，一步ema.average
2） 先apply，后average
3） apply里放的是一个list
4） Variable通过tf.assign改动

原理：

apply方法会为每个变量（也可以指定特定变量）创建各自的shadow variable， 即影子变量。之所以叫影子变量，是因为它会全程跟随训练中的模型变量。影子变量会被初始化为模型变量的值，然后，每训练一个step，就更新一次。更新的方式为：

应用例子：

import tensorflow as tf

v1 = tf.Variable(0, dtype=tf.float32) #初始化v1变量
step = tf.Variable(0, trainable=False) #初始化step为0
ema = tf.train.ExponentialMovingAverage(0.99, step) #定义平滑类，设置参数以及step
maintain_averages_op = ema.apply([v1]) #定义更新变量平均操作

with tf.Session() as sess:

    # 初始化
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print sess.run([v1, ema.average(v1)])

    # 更新变量v1的取值
    sess.run(tf.assign(v1, 5))
    sess.run(maintain_averages_op)
    print sess.run([v1, ema.average(v1)]) 

    # 更新step和v1的取值
    sess.run(tf.assign(step, 10000))  
    sess.run(tf.assign(v1, 10))
    sess.run(maintain_averages_op)
    print sess.run([v1, ema.average(v1)])       

    # 更新一次v1的滑动平均值
    sess.run(maintain_averages_op)
    print sess.run([v1, ema.average(v1)])

书中详细解释

四、批标准化：（batch normalization，BN)

https://www.cnblogs.com/zyly/p/8996070.html

（1）BN的来源：

批标准化（BN）是为了克服神经网络层数加深导致难以训练而产生的。

神经网络层数加深，收敛速度会很慢，常常导致梯度弥散或者梯度爆炸问题。

统计学中有一个ICS（Internal Covariate Shift）理论，这是一个经典假设：源域和目标域的数据分布是一致的。即训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好效果的一个基本保障。

【Covariate Shift：指训练集的样本数据和目标样本集分布不一致时，训练得到的模型无法很好地泛化，它是分布不一致假设之下的一个分支问题，即源域和目标域的条件概率是一致的，但其边缘概率不同。的确，神经网络的各层输出，输出分布和对应的输入分布不同，且差异随着网络深度增大而加大，但每一层所指向的样本标记（label）是不变的。】

解决思路：根据训练样本和目标样本的比例对训练样本做一个矫正。通过BN来规范化某些层或所有层的输入，来固定每层输入的均值与方差。

（2）BN方法：

BN一般用在激活函数之前，对x=Wu+b做规范化，使结果的均值为0，方差为1.让每一层的输入有一个稳定的分布会有利于网络的训练。

BN层的前向传播公式为：

 反向传播:

https://blog.csdn.net/pan5431333/article/details/78052867

（3）BN类型：

  • Batch Norm：统计每个通道上所有其他维度的均值和方差。

（4）BN优点：

详细解释:https://blog.csdn.net/sunflower_sara/article/details/81159155

BN通过规范化让激活函数分布在线性区间，结果就是加大了梯度，优点如下：

  1. 加大探索的步长，加快收敛速度
  2. 容易跳出局部最小值
  3. 破坏原来的数据分布，一定程度上缓解过拟合
  4. 降低网络对初始化权重敏感
  5. 允许使用较大的学习率

(5)BN缺点:

https://cloud.tencent.com/developer/article/1351476

  1. 如果Batch Size太小，则BN效果明显下降。
  2. 局限2：对于有些像素级图片生成任务来说，BN效果不佳；
  3. 局限3：RNN等动态网络使用BN效果不佳且使用起来不方便
  4. 局限4：训练时和推理时统计量不一致

（6）BN训练 \ 验证 \ inference

训练:

BN层执行的操作为前向传播，eps的作用是保证分母不会除零，计算每个featuremap的minibatch集内的均值方差，归一化每个神经元xi，也就是CNN中featuremap的每个像素点，然后乘一个系数r，加上偏置b(初始化时一般r=1,b=0)，得到输出yi，然后yi输入到激活函数，激活函数的输出再输入下一个卷积层，下一个卷积层的输出又重复以上操作。一般BN层都加在非线性层前面。参数r,b也是通过反向传播算法学习得到。所以在训练中，forward和backward都经过BN层。

按照：

 迭代更新全局训练数据的统计值𝜇𝑟和𝜎𝑟2，其中momentum 是需要设置一个超参数，用于平衡两者更新幅度。默认为0.99

验证\inference:

 在训练时，归一化输入用的是minibatch的均值方差，而实际上，整个训练集的均值方差是最能反映数据分布的，但是由于训练的计算量考虑，用随机抽取的minibatch也能大致反映数据的分布。但是到了测试的时候，输入只有一个，BN无法对一个输入归一化，所以在网络每次训练时，会保存每个minibatch的均值方差，在网络训练好之后，BN层的均值方差用之前训练用的所有minibatch对整个数据集的均值方差的无偏估计量来代替。r,b任然用仍然用训练得到的参数。

 

(7)BN两种情况:全连接\CNN

https://www.cnblogs.com/bonelee/p/8528464.html

(8) 代码示例：

三种情况:

  1. tf.nn.batch_normalization
  2. tf.layers.batch_normalization [推荐]
  3. tf.contrib.layers.batch_norm [推荐]

使用tf.nn.batch_normalization:

    • 加入 is_training 参数
    • 去除bias 以及激活函数
    • 添加 gamma,beta,pop_mean，pop_variance变量
    • 使用 tf.cond处理训练与测试的不同
    • tf.nn.moments计算均值和方差。with tf.control_dependencies... 更新population statistics,tf.nn.batch_normalization 归一化层的输出
    • 在测试时，用tf.nn.batch_normalization归一化层的输出，使用训练时候的population statistics
      -加入激活函数

m = K.mean(X, axis=-1, keepdims=True)        #计算均值  
std = K.std(X, axis=-1, keepdims=True)           #计算标准差  
X_normed = (X - m) / (std + self.epsilon)         #归一化  
out = self.gamma * X_normed + self.beta           #重构变换

 使用tf.layers.batch_normalization [推荐]:

CNN的实战代码:https://www.01hai.com/note/av147588

https://www.cnblogs.com/cloud-ken/p/9314711.html

　　全连接\CNN:

  • 加入 is_training 参数
  • 从全连接层中移除激活函数和bias
  • 使用tf.layers.batch_normalization函数 归一化层的输出
  • -传递归一化后的值给激活函数

　　但比较两者的区别，当你使用tf.layers时，对全连接层和卷积层时基本没有区别，使用tf.nn的时候，会有一些不同 。
一般来说，人们同意消除层的bias(因为批处理已经有了扩展和转换)，并在层的非线性激活函数之前添加batch normalization。然而，对一些网络来说，使用其他方式也能很好工作。

在train方面，需要修改：

  • 添加is_training ,一个占位符储存布尔量，表示网络是否在训练。
  • 传递is_training给卷积层和全连接层
  • 每次调用session.run(),都要给feed_dict传递合适的值
  • 将train_opt放入tf.control_dependencies(tf.get_collection(tf.GraphKeys.UPDATE_OPS)):下

训练的时候需要注意两点，(1)输入参数training=True,(2)计算loss时，要添加以下代码（即添加update_ops到最后的train_op中）。这样才能计算μ和σ的滑动平均（测试时会用到）

##在网络结构中,将该参数设置为占位符,在inference时可传入值False
self.is_training = tf.placeholder(tf.bool,name="is_training")

def batch_norm(x, momentum=0.9, epsilon=1e-5, train=True, name='bn'):
      return tf.layers.batch_normalization(x,
                              momentum=momentum,
                              epsilon=epsilon,
                              scale=True,
                              training=train,
                              name=name)

with tf.name_scope("output"):
    W = tf.get_variable(
        "W",
        shape=[num_filters_total, num_classes],
        initializer=tf.contrib.layers.xavier_initializer())
    b = tf.Variable(tf.constant(0.1, shape=[num_classes]), name="b")
    l2_loss += tf.nn.l2_loss(W)
    l2_loss += tf.nn.l2_loss(b)
    W_matmul_x = tf.matmul(self.h_drop,W) ##注意这个把biase去掉
#             Wx_plus_b = tf.nn.xw_plus_b(self.h_drop, W, b, name="scores")

##注意train在训练时设置为True,验证和inference时设置为False
    # BN 
    if self.use_batch_norm:
        fn_output = batch_norm(W_matmul_x,train=self.is_training)
    else:
        fn_output = W_matmul_x + b

    self.scores = tf.sigmoid(fn_output, name="sigmoid_scores")
    self.predictions = tf.cast(self.scores > 0.5, tf.int64,name = "predictions")

训练时记得添加以下代码:

 update_op = tf.get_collection(tf.GraphKeys.UPDATE_OPS)
 with tf.control_dependencies(update_op):
    train_op = optimizer.minimize(loss)

测试时:

# inference
def inference(input_data,file):
    graph = tf.Graph()
    with graph.as_default():
        os.environ["CUDA_VISIBLE_DEVICES"] = "1"
        config = tf.ConfigProto()
        config.gpu_options.allow_growth = True
        sess = tf.Session(config=config)
        with sess.as_default():
            saver = tf.train.import_meta_graph(file + '.meta')
            saver.restore(sess, file)
            input_x = graph.get_operation_by_name("input_x").outputs[0]
            scores = graph.get_operation_by_name("output/sigmoid_scores").outputs[0]
            dropout_keep_prob = graph.get_operation_by_name("dropout_keep_prob").outputs[0]
###将is_training的占位符参数传入
            is_training = graph.get_operation_by_name("is_training").outputs[0]
            pred = scores.eval(feed_dict={input_x: input_data, dropout_keep_prob: 1.0,is_training:False})
            print('pred_split:',pred[:10])
    return pred

 

posted on 2018-11-27 21:43  吱吱了了  阅读(956)  评论(0)    收藏  举报

导航