Hall 定理

Hall 定理

---

其实很多是和其他结合的，但是大部分难点都在用上 hall 吧

P3488：根据 Hall 定理，知道对于任意一些号码的人，总要有大于等于他们人数的鞋与之匹配。因为取相邻号码是最劣的，所以只要保证 $ sum_{l,r} \leq (r-l+1+d) \cdot k $ 就绝对有完美匹配。令 $s_{l,r}= \sum_{i=l}^{r}{a_i-k} $ 则可以将式子转化为 $ s_{l,r} \leq d k $，线段树动态维护最大子段和即可。

P10208：将 \(A_i\) 视为左部点，$ B_i $ 视为右部点，对于所有 \(A_i\)，向所有 \(B_i \leq A_i\) 且 \(i \neq j\) 连边，求是否有完美匹配。根据 Hall 定理，对于任意大小为 \(k\) 的左部点集合，其邻域大小必须大于等于 \(k\)。

先考虑极端情况，将所有 \(A_i,B_i\) 视为一段区间，则对于最大的 \(A_i\)，若 \([A_i,B_i]\) 与其他区间无交就绝对没有完美匹配。考虑推广，对于任意 \([A_i,B_i]\) 都与其他区间有交就有完美匹配。题解区大神的证明。

记一个与区间 \([A_i,B_i]\) 相交的，在其左侧且下标最接近的区间的下标为 \(L_i\)，右边的为 \(R_i\)。则对于一个询问，没有完美匹配当且仅当存在 $ L_i < l \leq i \leq r \leq R_i $。

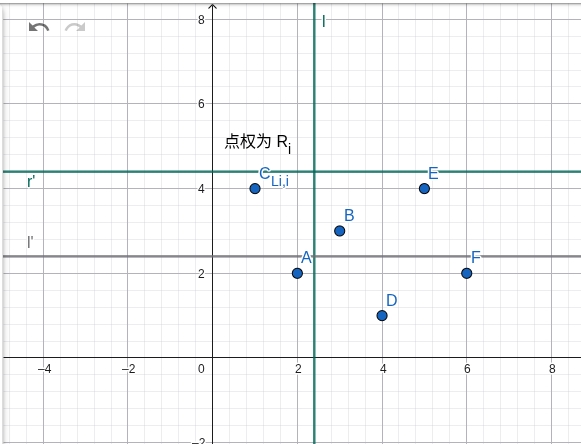
考虑维护 \(L_i,R_i\)。下标从小到大加入线段树，区间查询下标最大/最小值，再区间修改 \(A_i,B_i\) 为 \(i\) 即可。如何求是否存在 $ L_i < l \leq i \leq r \leq R_i $。将询问离线，按 \(l\) 排序，线段树加入所有 \(L_i < l\) 的区间，下标为 \(i\)，存储的值为 \(R_i\)。因为已经自然地满足了 \(L_i < l\)，所以查询 \([l,r]\) 中的最大值，即图中 \(l,l',r'\) 围住的区域中取最大点权。如果大于等于 \(r\) 就是无解，否则有解。