统计学习——KNN
1.KNN基本介绍
KNN,又叫K近邻法(k-nearest neighbor),是一种基本分类与回归方法,这点和决策树算法相同。
它的基本原理是“物以类聚”,如果空间中某些样本具有近似的特征属性,则将它们归为一类,于是,训练数据集便把特征空间进行了划分,当有新的输入进来时,便去寻找和它最相似的k个样本,看这k个样本大多数属于哪一个类别,便把新的输入归为该类别。
KNN做回归和分类的主要区别在于最后做预测时候决策方式不同。KNN做分类预测时,一般是选择多数表决法,即训练集和预测的样本特征最近的k个样本,预测为里面有最多类别数的类别。而KNN在做回归的时候,一般是选择平均法,即最近的k个样本的样本输出的平均值作为回归预测值。两者区别不大,本文主要讲解KNN的分类方法,但思想对KNN的回归方法也适用,由于scikit-learn里只使用了蛮力实现(brute-force),KD树实现(KDTree)和球树(BallTree)实现,本文只讨论这几种算法的实现原理。其余的实现方法比如BBF树,MVP树等,在这里不做讨论。
2.KNN算法
k近邻算法简单、直观:给定一个训练数据集,对新的输入实例,在训练数据集中找到与该实例最邻近的k个实例,这k个实例的多数属于某一类,就把该输入实例分为这个类。下面先叙述k近邻算法,然后在讨论细节。
算法(knn)
输入:训练数据集
其中,\(x_i\in x \subseteq R^n\)为实例的特征向量,\(y_i \in Y = \{c_1,c_2,···,c_k\}\)为实例的类别,\(x\)为输入实例
输出:实例\(x\)所属的类\(y\)
(1) 根据给定的距离度量,在训练集\(T\)中找出与\(x\)最邻近的\(k\)个点,涵盖这\(k\)个点的\(x\)的邻域记作\(N_k(x)\);
(2) 在\(N_k(x)\)中根据分类决策规则(如多数表决)决定\(x\)的类别\(y\):
这个公式实现的就是如果k个实例的多数属于某一类,就把该输入实例分为这个类。
k近邻法的特殊情况是\(k=1\),称为最近邻算法。对于输入的实例点\(x\),最近邻法将训练数据集中与\(x\)最近邻点的类作为\(x\)的类。
注意:k近邻法没有显示的学习过程。
3.KNN模型
3.1模型
k近邻法,模型确定通常需要确定三个条件,即距离度量(如欧式距离)、k值、分类决策规则(如多数表决)。当这三个条件确定后,模型的预测方式也就确定了,便可以对任何一个新的输入实例,它所属的类唯一地确定。其实就是通过上述的三个条件将特征空间划分为一些子空间,确定子空间里的每个点所属的类
3.2距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映。k近邻模型的特征空间一般是\(n\)维实数向量空间\(R^n\)。使用的距离是欧式距离,也可以是其他距离,如更一般的\(L_p\)距离。
设特征空间\(x\in R^n\),\(x_i,x_j\in X\),\(x_i = (x_i^{(1)},x_i^{(2)},···,x_i^{(n)})^T,x_j = (x_j^{(1)},x_j^{(2)},···,x_j^{(n)})^T\),\(x_i,x_j\)的\(L_p\)距离定义为
这里\(p\geq1\)。当\(p=2\)时,称为欧式距离;当\(p=1\)时,称为曼哈顿距离。当\(p=\infty\),它是各个坐标距离的最大值,即
如图给出了二维空间中p取不同值,与原点的\(L_p\)距离为1的点的图形。
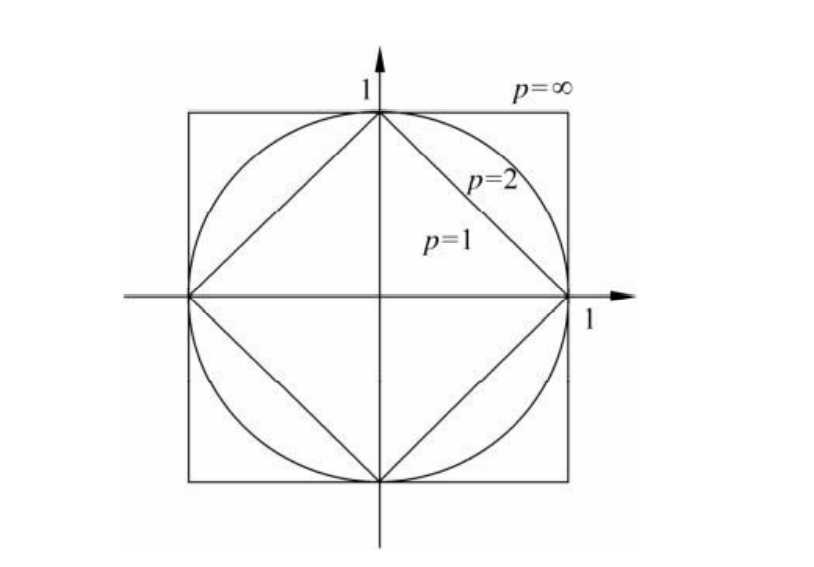
例子:已知二维空间的三个点\(x_1 = (1,1)^T,x_2 = (5,1)^T,x_3 = (4,4)^T\),试求在p取不同值时,\(L_p\)距离下\(x_1\)的最近邻点。
解:因为\(x_1,x_2\)只有第一维上值不同,所以\(p\)为任何值时,\(L_p(x_1,x_2) = 4\)。而
于是得到:\(p=1~or~p=2\),\(x_2\)是\(x_1\)的最近邻点;\(p\geq3\),\(x_3\)是\(x_1\)的最近邻点。
3.3\(~\)k值选择
k值的选择会对k近邻法的结果产生重大影响。如果选择较小的k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。但缺点是“学习”的估计误差会增大,预测结果会对近邻的实例点非常敏感。如果邻近的实例点恰巧是噪声,预测就会出错。换句话说,k值的减小就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的k值,就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差。但缺点是学习的近似误差会增大。这时与输入实例较远的(不相似的)训练实例也会对预测起作用,使预测发生错误。k值的增大就意味着整体的模型变得简单,会发生模型的欠拟合。
如果k=N,那么无论输入实例是什么,都将简单地预测它属于在训练实例中最多的类。这时,模型过于简单,完全忽略训练实例中的大量有用信息,是不可取的。
在应用中,k值一般取一个比较小的数值。通常采用交叉验证法来选取最优的k值。
3.4分类决策规则
k近邻法中的分类决策规则往往是多数表决,即由输入实例的k个邻近的训练实例中的多数类决定输入实例的类。
4.KNN算法实现方式
4.1暴力实现
计算预测样本到所有训练集样本的距离,然后选择最小的k个距离即可得到k个最近邻点。缺点在于当特征数比较多、样本数比较多的时候,算法的执行效率比较低。
代码实现python:
取load_iris数据集中的sepal length,sepal width作为两大类,作为输入实例
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from collections import Counter
# data
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
# data = np.array(df.iloc[:100, [0, 1, -1]])
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()
data = np.array(df.iloc[:100, [0, 1, -1]])
X, y = data[:,:-1], data[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
class KNN:#Brute-force
def __init__(self, X_train, y_train, n_neighbors=3, p=2):
"""
parameter: n_neighbors 临近点个数,这里取3
parameter: p 距离度量
"""
self.n = n_neighbors
self.p = p
self.X_train = X_train
self.y_train = y_train
def predict(self, X):
# 取出n个点
knn_list = []
for i in range(self.n):#初始化,先取训练数据中的前3个样本,存入knn_list列表中
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)#求L2距离
knn_list.append((dist, self.y_train[i]))
for i in range(self.n, len(self.X_train)):#取列表中dist最大值与后面逐个比较
max_index = knn_list.index(max(knn_list, key=lambda x: x[0]))
dist = np.linalg.norm(X - self.X_train[i], ord=self.p)
if knn_list[max_index][0] > dist:#如果此时存在比列表中小的dist,则进表,
knn_list[max_index] = (dist, self.y_train[i])
# 统计
knn = [k[-1] for k in knn_list]
count_pairs = Counter(knn)#统计词频
# max_count = sorted(count_pairs, key=lambda x: x)[-1]
max_count = sorted(count_pairs.items(), key=lambda x: x[1])[-1][0]#这里是升序排序,最后要取列表中最后一个的第一个元素,即类别数最大的类别
return max_count
def score(self, X_test, y_test):#计算测试集的准确率
right_count = 0
n = 10
for X, y in zip(X_test, y_test):
label = self.predict(X)
if label == y:
right_count += 1
return right_count / len(X_test)
clf = KNN(X_train, y_train)
print(clf.score(X_test,y_test))
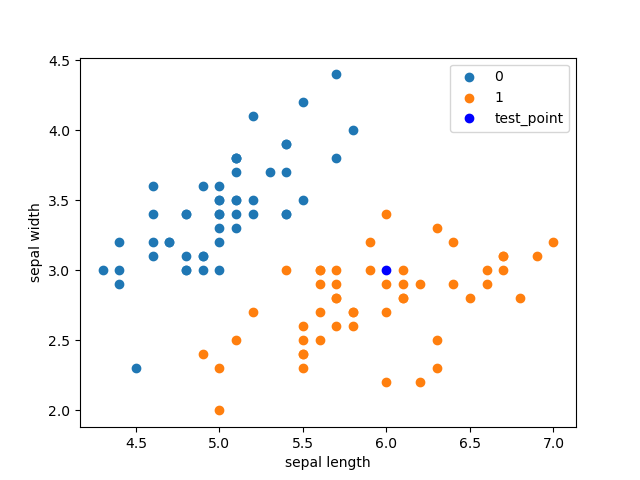
test_point = [6.0, 3.0]
print('Test Point: {}'.format(clf.predict(test_point)))
plt.scatter(df[:50]['sepal length'], df[:50]['sepal width'], label='0')
plt.scatter(df[50:100]['sepal length'], df[50:100]['sepal width'], label='1')
plt.plot(test_point[0], test_point[1], 'bo', label='test_point')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()
4.2\(~\)KD树
为了提高k近邻搜索的效率,可以考虑使用特殊的结构存储训练数据,以减少计算距离的次数。下面介绍kd树的方法
kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树,表示对k维空间的一个划分。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分,构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。
kd树算法包括三步,第一步是建树,第二步是搜索最近邻,最后一步是预测。
4.2.1构造kd树
构造kd树的方法如下:kd树建树采用从m个样本的n维特征中,分别计算n个特征取值的方差,用方差最大的第k维特征\(n_k\)来作为根节点。对于这个特征,我们选择这m个样本的\(n_k\)特征,进行排序,得中位数\(n_{kv}\)所对应的样本作为划分点,对于所有第k维特征的取值小于\(n_{kv}\)的样本,我们划入左子树,对于第k维特征的取值大于等于\(n_{kv}\)的样本,我们划入右子树,然后对于左右子树,采用同样的办法来求方差最大的特征来做根结点,递归的生成kd树。
具体流程如下图:
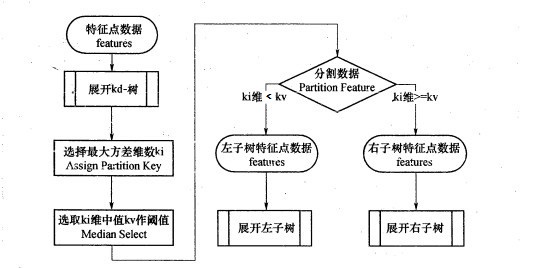
书上是依次选择特征\(\{x^{(1)},x^{(2)},···,x^{(n)}\}\)对空间切分,选择训练实例点在选定坐标轴上的中位数为切分点,并没有做方差比较,这样得到的kd树是平衡的。注意,平衡的kd树搜索时的效率未必是最优的。
kd树算法
输入:k维空间数据集\(T = \{x_1,x_2,···,x_m\}\),\(x_i \in R^n\)
(1) 开始:构造根节点,具体方法计算每一维的方差,选择方差最大的维数\(k\)为坐标轴,找所有实例\(x^{(k)}\)坐标的中位数为切分点,然后切分由通过切分点并与坐标轴\(x^{(k)}\)垂直的超平面实现,根节点的切分将对应的超矩形区域切分为两个子区域。
由根节点生成深度为1的左右子节点:左节点对应坐标\(x^{(k)}\)小于切分点的子区域,右子节点对应于坐标\(x^{(k)}\)大于等于切分点的子区域。将落在切分超平面上的实例点保存在根结点。
(2) 重复:对左右子树按照(1)的方法继续构造
(3) 直到两个子区域没有实例存在时停止。从而形成kd树的区域划分。
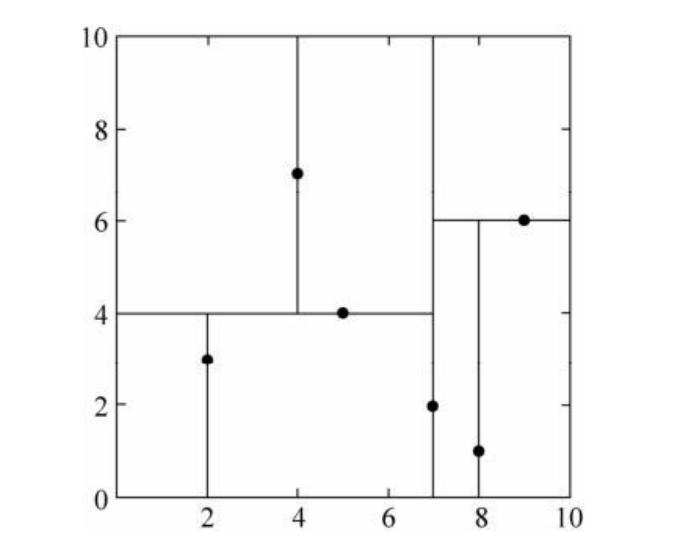
例子:给定一个二维空间的数据集:
构造一个kd树
解:
(1)先找根节点,6个数据点在x,y维度上的数据方差为6.97,5.37,所以在x轴上方差更大,用第1维特征建树,按照第1维进行排序,即:
确定划分点是\((7,2)^T\),这样,该节点的分割超平面就是通过\((7,2)^T\),并垂直于x轴。
(2)确定左右子树。分割超平面\(x=7\)将整个空间分为两部分:\(x<7\)的部分为左子树,包含3个结点\(\{(2,3)^T,(5,4)^T,(4,7)^T\}\);另一部分为右子树,包含2个结点\(\{(9,6)^T,(8,1)^T\}\)
(3)用同样的办法划分左右子树。最终得到kd树。
4.2.2\(~\)kd树搜索最近邻
下面介绍如何利用kd树进行k近邻搜索。这里介绍最近邻为例。
当kd树建好后,给定一个目标点,我们首先在kd树里面找到包含目标点的叶子节点。以目标点为圆心,以目标点到叶子节点样本实例的距离为半径,得到一个超球体,最近邻点一定在这个超球体内部。然后返回叶子节点的父节点,检查该父节点包含的超平面是否和超球体相交,如果相交就到这个父节点的另一个子节点寻找是否有更加近的点,如果不相交,就在另一个子树继续搜索最近邻。当回溯到根节点时,算法结束,此时保存的最近邻点就是最终的最近邻。
从上面可以看出,kd树划分后可以大大减少无效的最近里搜索,很多样本由于所在的超平面和超球体不相交,根本不需要计算距离。大大节省了计算时间。
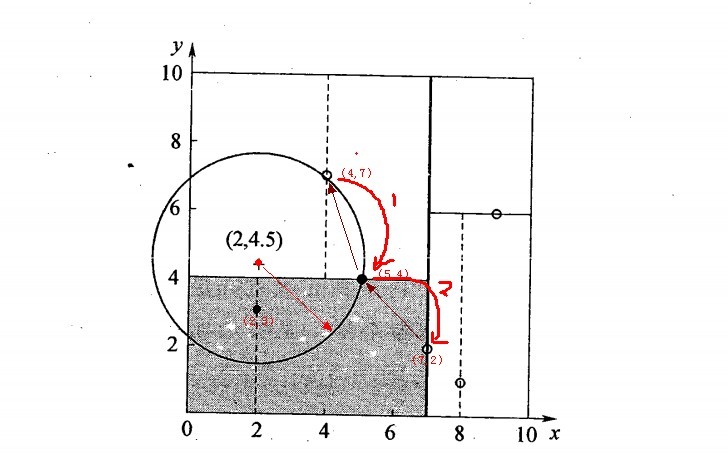
我们用4.2.1建立的kd树,来找点\((2,4.5)^T\)的最近邻。
先进行二叉查找,先从\((7,2)^T\)查找到\((5,4)^T\)节点,在进行查找时是由\(y = 4\)为分割超平面,由于查找点为y值为\(4.5\),因此进入右子空间查找到\((4,7)^T\),形成搜索路径\(<(7,2)^T,(5,4)^T,(4,7)^T>\),但 \((4,7)^T\)与目标查找点的距离为\(3.202\),而\((5,4)^T\)与查找点之间的距离为\(3.041\),所以\((5,4)^T\)为查询点的最近点; 以\((2,4.5)^T\)为圆心,以\(3.041\)为半径作圆,如下图所示。可见该圆和\(y = 4\)超平面交割,所以需要进入\((5,4)^T\)左子空间进行查找,也就是将\((2,3)^T\)节点加入搜索路径中得\(<(7,2)^T,(5,4)^T,(4,7)^T,(2,3)^T>\);于是接着搜索至\((2,3)^T\)叶子节点,\((2,3)^T\)距离\((2,4.5)^T\)比\((5,4)^T\)要近,所以最近邻点更新为\((2,3)^T\),最近距离更新为\(1.5\);回溯查找至\((5,4)^T\),直到最后回溯到根结点\((7,2)^T\)的时候,以\((2,4.5)^T\)为圆心\(1.5\)为半径作圆,并不和\(x = 7\)分割超平面交割,如下图所示。至此,搜索路径回溯完,返回最近邻点\((2,3)\),最近距离\(1.5\)。
4.2.3kd树预测
有了kd树搜索最近邻的方法,kd树预测就很简单了,在kd树搜索最近邻的基础上,我们已经求得第一个最近邻样本,就把它置为已选。在第二轮中,我们忽略为已选的样本,重新run,求得第二个最近邻样本,再把它置为已选。这样跑k次,就得到了目标的k个最近邻,然后根据多数表决法,如果是KNN分类,预测为k个最近邻里面有最多类别数的类别,如果是KNN回归,用k个最近邻样本输出的平均值作为回归预测值。
算法(kd树的最近邻搜索)
输入:已构造的kd树;目标点x;
输出:x的最近邻。
(1) 在kd树中找出包含目标点x的叶节点:从根节点出发,递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标,则移动到左子节点,否则移动到右子节点。直到子节点为叶节点为止。
(2) 以此叶节点为“当前最近点”。
(3) 递归地向上回退,在每个节点进行一下操作:
(a)如果该节点保存的实例点比当前最近点距离目标点更近,则以该实例点为“当前最近点”。
(b)目标最近点可能存在于该节点另一个子节点对应的区域。检查该子节点的父节点的另一子节点对应的区域是否有更近的点。具体地,检查另一子节点对应的区域是否与以目标点为球心、以目标点与“当前最近点”间的距离为半径的超球体相交。
如果相交,可能在另一个子节点对应的区域内存在距目标点更近的点,移动到另一个子节点。接着,递归地进行最近邻搜索;
如果不相交,向上回退。
(4) 当回退到根结点时,搜索结束。最后的“当前最近点”即为x的最近邻点。
如果实例点是随机分布,kd树搜索的平均计算复杂度是\(O(logN)\),这里\(N\)是训练实例数。kd树更适用于训练实例数远大于空间维数时的k近邻搜索。当空间维数接近训练实例数时,退化成线性扫描;
4.2.3 kd树代码实战
# kd-tree每个结点中主要包含的数据结构如下
class KdNode(object):
def __init__(self, dom_elt, split, left, right):
self.dom_elt = dom_elt # k维向量节点(k维空间中的一个样本点)
self.split = split # 整数(进行分割维度的序号)
self.left = left # 该结点分割超平面左子空间构成的kd-tree
self.right = right # 该结点分割超平面右子空间构成的kd-tree
class KdTree(object):
def __init__(self, data):
k = len(data[0]) # 数据维度
def CreateNode(split, data_set): # 按第split维划分数据集data_set创建KdNode
if not data_set: # 数据集为空
return None
data_set.sort(key=lambda x: x[split]) # 按要进行分割的那一维数据排序
split_pos = len(data_set) // 2 # 求中位数
median = data_set[split_pos] # 中位数分割点
split_next = (split + 1) % k # 循环重复求下一个分割点
# 递归的创建kd树
return KdNode(
median,
split,
CreateNode(split_next, data_set[:split_pos]), # 创建左子树
CreateNode(split_next, data_set[split_pos + 1:])) # 创建右子树
self.root = CreateNode(0, data) # 从第0维分量开始构建kd树,返回根节点
# KDTree的前序遍历
def preorder(root):
print(root.dom_elt)
if root.left: # 节点不为空
preorder(root.left)
if root.right:
preorder(root.right)
# 对构建好的kd树进行搜索,寻找与目标点最近的样本点:
from math import sqrt
from collections import namedtuple
# 定义一个namedtuple,分别存放最近坐标点、最近距离和访问过的节点数
result = namedtuple("Result_tuple",
"nearest_point nearest_dist nodes_visited")
def find_nearest(tree, point):
k = len(point) # 数据维度
def travel(kd_node, target, max_dist): # target 目标点
if kd_node is None: # kd树空,不存在
return result([0] * k, float("inf"),
0) # python中用float("inf")和float("-inf")表示正负无穷
nodes_visited = 1
s = kd_node.split # 进行分割的维度,一开始是第0维
pivot = kd_node.dom_elt # 进行分割的“轴”
if target[s] <= pivot[s]: # 如果目标点第s维小于分割轴的对应值(目标离左子树更近)
nearer_node = kd_node.left # 下一个访问节点为左子树根节点
further_node = kd_node.right # 同时记录下右子树
else: # 目标离右子树更近
nearer_node = kd_node.right # 下一个访问节点为右子树根节点
further_node = kd_node.left
temp1 = travel(nearer_node, target, max_dist) # 进行遍历找到包含目标点的区域
nearest = temp1.nearest_point # 找到以此叶结点作为“当前最近点”
dist = temp1.nearest_dist # 更新最近距离
nodes_visited += temp1.nodes_visited
if dist < max_dist:
max_dist = dist # 最近点将在以目标点为球心,max_dist为半径的超球体内
#----------------------------------------------------------------------
# 计算目标点与分割点的欧氏距离
temp_dist = sqrt(sum((p1 - p2)**2 for p1, p2 in zip(pivot, target)))
if temp_dist < dist: # 如果“更近”
nearest = pivot # 更新最近点
dist = temp_dist # 更新最近距离
max_dist = dist # 更新超球体半径
# 检查另一个子结点对应的区域是否有更近的点
temp2 = travel(further_node, target, max_dist)
nodes_visited += temp2.nodes_visited
if temp2.nearest_dist < dist: # 如果另一个子结点内存在更近距离
nearest = temp2.nearest_point # 更新最近点
dist = temp2.nearest_dist # 更新最近距离
return result(nearest, dist, nodes_visited)
return travel(tree.root, point, float("inf")) # 从根节点开始递归
data = [[2,3],[5,4],[9,6],[4,7],[8,1],[7,2]]
kd = KdTree(data)
print(preorder(kd.root))
ret = find_nearest(kd, [3,4.5])
print (ret)
[7, 2]
[5, 4]
[2, 3]
[4, 7]
[9, 6]
[8, 1]
Result_tuple(nearest_point=[2, 3], nearest_dist=1.8027756377319946, nodes_visited=4)
from time import perf_counter
from random import random
# 产生一个k维随机向量,每维分量值在0~1之间
def random_point(k):
return [random() for _ in range(k)]
# 产生n个k维随机向量
def random_points(k, n):
return [random_point(k) for _ in range(n)]
N = 400000
t0 = perf_counter()
kd2 = KdTree(random_points(3, N)) # 构建包含四十万个3维空间样本点的kd树
ret2 = find_nearest(kd2, [0.1,0.5,0.8]) # 四十万个样本点中寻找离目标最近的点
t1 = perf_counter()
print ("time: ",t1-t0, "s")
print (ret2)
time: 5.4623788 s
Result_tuple(nearest_point=[0.09929288205798159, 0.4954936771850429, 0.8005722800665575], nearest_dist=0.004597223680778027, nodes_visited=42)
4.3球数(Ball Tree)
球树,顾名思义,就是每个分割块都是超球体,而不是kd树里的超平面
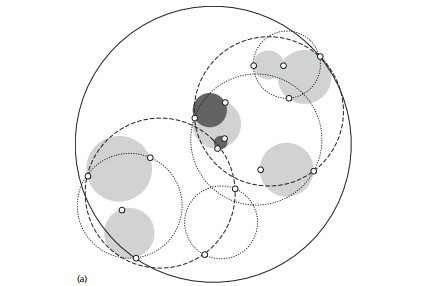
具体的建树流程:
(1) 先构建一个超球体,这个超球体是可以包含所有样本的最小球体。
(2) 从球中选择一个离球的中心最远的点,然后选择第二个点离第一个点最远,将球中所有的点分配到离这两个聚类中心最近的一个上,然后计算每个聚类的中心,以及聚类能够包含它所有数据点所需的最小半径。这样我们得到了两个子超球体,和KD树里面的左右子树对应。
(3)对于这两个子超球体,递归执行步骤(2)。 最终得到了一个球树。
可以看出KD树和球树类似,主要区别在于球树得到的是节点样本组成的最小超球体,而KD得到的是节点样本组成的超平面,这个超球体要与对应的KD树的超平面小,这样在做最近邻搜索的时候,可以避免一些无谓的搜索。
4.3.1球树搜索最近邻
使用球树找出给定目标点的最近邻方法是首先自上而下贯穿整棵树找出包含目标点所在的叶子,并在这个球里找出与目标点最邻近的点,这将确定出目标点距离它的最近邻点的一个上限值,然后跟KD树查找一样,检查兄弟结点,如果目标点到兄弟结点中心的距离超过兄弟结点的半径与当前的上限值之和,那么兄弟结点里不可能存在一个更近的点;否则的话,必须进一步检查位于兄弟结点以下的子树。
检查完兄弟节点后,我们向父节点回溯,继续搜索最小邻近值。当回溯到根节点时,此时的最小邻近值就是最终的搜索结果。
从上面的描述可以看出,KD树在搜索路径优化时使用的是两点之间的距离来判断,而球树使用的是两边之和大于第三边来判断,相对来说球树的判断更加复杂,但是却避免了更多的搜索,这是一个权衡。
5.KNN算法的扩展
这里再讨论下KNN算法的扩展,限定半径最近邻算法。
有时候我们会遇到这样的问题,即样本中某系类别的样本非常的少,甚至少于K,这导致稀有类别样本在找K个最近邻的时候,会把距离其实较远的其他样本考虑进来,而导致预测不准确。为了解决这个问题,我们限定最近邻的一个最大距离,也就是说,我们只在一个距离范围内搜索所有的最近邻,这避免了上述问题。这个距离我们一般称为限定半径。
接着再讨论下另一种扩展,最近质心算法。这个算法比KNN还简单。它首先把样本按输出类别归类。对于第 \(L\)类的\(C_l\)个样本。它会对这\(C_l\)个样本的\(n\)维特征中每一维特征求平均值,最终该类别所有维度的\(n\)个平均值形成所谓的质心点。对于样本中的所有出现的类别,每个类别会最终得到一个质心点。当我们做预测时,仅仅需要比较预测样本和这些质心的距离,最小的距离对于的质心类别即为预测的类别。这个算法通常用在文本分类处理上。
6.scikit-learn中KNN库
在scikit-learn 中,与近邻法这一大类相关的类库都在sklearn.neighbors包之中。KNN分类树的类是KNeighborsClassifier,KNN回归树的类是KNeighborsRegressor。除此之外,还有KNN的扩展,即限定半径最近邻分类树的类RadiusNeighborsClassifier和限定半径最近邻回归树的类RadiusNeighborsRegressor, 以及最近质心分类算法NearestCentroid。
在这些算法中,KNN分类和回归的类参数完全一样。限定半径最近邻法分类和回归的类的主要参数也和KNN基本一样。
比较特别是的最近质心分类算法,由于它是直接选择最近质心来分类,所以仅有两个参数,距离度量和特征选择距离阈值,比较简单,因此后面就不再专门讲述最近质心分类算法的参数。
另外几个在sklearn.neighbors包中但不是做分类回归预测的类也值得关注。kneighbors_graph类返回用KNN时和每个样本最近的K个训练集样本的位置。radius_neighbors_graph返回用限定半径最近邻法时和每个样本在限定半径内的训练集样本的位置。NearestNeighbors是个大杂烩,它即可以返回用KNN时和每个样本最近的K个训练集样本的位置,也可以返回用限定半径最近邻法时和每个样本最近的训练集样本的位置,常常用在聚类模型中。
下面介绍常用的基本用法,若想查看更多资料,推荐scikit-learn 中KNN相关的类库
from sklearn.neighbors import KNeighborsClassifier
clf_sk = KNeighborsClassifier()
clf_sk.fit(X_train, y_train)
## KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
## metric_params=None, n_jobs=None, n_neighbors=5, p=2,
## weights='uniform')
- n_neighbors: 临近点个数
- p: 距离度量
- algorithm: 近邻算法,可选{'auto', 'ball_tree', 'kd_tree', 'brute'}
- weights: 确定近邻的权重
6.总结与参考文献
k近邻法是基本且简单的分类与回归方法。思想不难理解,但是算法优化,kd树构建之类就显得稍微复杂,特别是底层原理代码时,变量多,关系有点难理解。这里总结下KNN的优缺点:
KNN的主要优点:
(1) 理论成熟,思想简单,既可以用来做分类也可以用来做回归
(2) 可用于非线性分类
(3) 训练时间复杂度比支持向量机之类的算法低,仅为O(n)
(4) 和朴素贝叶斯之类的算法比,对数据没有假设,准确度高,对异常点不敏感
(5) 由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合
(6) 该算法比较适用于样本容量比较大的类域的自动分类,而那些样本容量较小的类域采用这种算法比较容易产生误分
主要缺点:
(1) 计算量大,尤其是特征数非常多的时候
(2) 样本不平衡的时候,对稀有类别的预测准确率低
(3) KD树,球树之类的模型建立需要大量的内存
(4) 使用懒散学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
(5) 相比决策树模型,KNN模型可解释性不强
1.《统计学习方法》(李航)
2.刘建平老师机器学习博客

 统计学习——knn
统计学习——knn

 浙公网安备 33010602011771号
浙公网安备 33010602011771号