20251222 - 强连通分量 总结
强连通分量
连通性的定义
-
无向图:
- 连通:任意两点之间都可达。
- 点双连通:任意删去一点之后任意两点之间还可达。
- 边双连通:任意删去一边之后任意两点之间还可达。
-
有向图:
- 弱连通:一个有向图把边替换成无向边后可以得到一张连通图。
- 强连通:一个有向图在有向情况下就是一张连通图。
强连通分量
从原图中选出一些节点和一些边构成的图,叫做这个原图的子图。
而如果该子图为连通图,则这个子图被称为连通子图。
一个连通子图的节点数和边数都极大,则成它为极大连通子图。
极大强连通子图被称为强连通分量,即 Strongly Connected Components,简称为 SCC。
DFS 树
DFS 树,又称为 DFS 生成树、DFS 搜索树,为遍历一张图的过程中,第一次到达每个点的每条边组成的树,根节点不算。
下图就是一张 DFS 树的示例图:
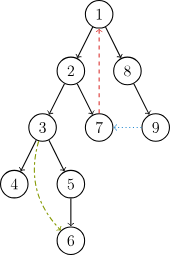
在有向图中,与 DFS 树有关的有四类边:
- 树边(上图中黑色实线),从父节点指向还没有被访问的子节点。
- 反祖边(上图中红色虚线),从子孙节点指向祖先节点的边。
- 前向边(上图中绿色虚线),指向子树中的边。
- 横叉边(上图中蓝色虚线),指向已经访问过但既不是祖先节点也不是子树中的边。
注意,前向边和横叉边只在有向图的 DFS 树中存在,无向图中只有树边和返祖边。
强连通分量求解结论
DFS 树和强连通分量的关系有一条结论:对于一个 SCC 中最先被搜到的点 \(u\),这个 SCC 中剩余的其他节点一定都在以 \(u\) 为根的子树中。
证明:
采用反证法。
对于这个 SCC 中的点 \(v\),假设点 \(v\) 不在以 \(u\) 为根的子树中。那么 \(u\) 到 \(v\) 的路径上一定有不包含在这个子树内的边,即横叉边或返祖边。这都要求指向的节点已经被访问过。
因为 \(u\) 和 \(v\) 在同一个 SCC 中,那么访问这些更早被访问的点时肯定能访问到 \(u\),这和 \(u\) 是最先被搜到的矛盾。
得证。
依据该结论求解强连通分量的算法叫做 Tarjan。
具体实现时,为了能快速取到被访问过节点的信息,我们采用栈(即 stack)存储所有被访问过的节点编号,找 SCC 时就取出连续一段来。
void Tarjan(int u){
f[u]=(++cnt),id[u]=f[u];
st.push(u),vis[u]=1;
for(int v:g[u])
if(!id[v])Tarjan(v),f[u]=min(f[u],f[v]);
else if(vis[v])f[u]=min(f[u],id[v]);
if(f[u]==id[u]){
vector<int> tmp;tmp.clear();
while(tmp.empty()||tmp.back()!=u)
vis[st.top()]=0,tmp.pb(st.top()),st.pop();
SCCs[++tot]=tmp;
}return;
}
缩点
在某些图论问题中,我们可以把一个 SCC 缩成一个点,这样就可以把原图转化为一个有向无环图,即 DAG,这样处理起来就会更加方便。
缩点时要注意原图中的边和新图中的边的对应关系。
代码就不放了。
边双连通分量
如果把强连通分量中的有向边替换成无向边,我们就得到了边双连通分量。
因为强连通分量中任意两点 \(u,v\),都有 \(u \to v\) 和 \(v \to u\) 两条路径,那么替换成无向边之后,任意两点之间都有至少两条不同的路径。
称边双连通为 BCC。
具体实现上与求 SCC 十分类似。
void Tarjan(int u,int fa){
f[u]=(++cnt),id[u]=f[u];
st.push(u),vis[u]=1;bool flag=0;
for(int v:g[u]){
if(v==fa){
if(flag)f[u]=min(f[u],id[v]);
else flag=1;continue;
}if(!id[v])Tarjan(v,u),f[u]=min(f[u],f[v]);
else if(vis[v])f[u]=min(f[u],id[v]);
}if(f[u]==id[u]){
vector<int> tmp;tmp.clear();
while(tmp.empty()||tmp.back()!=u)
vis[st.top()]=0,tmp.pb(st.top()),st.pop();
SCCs[++tot]=tmp;
}return;
}
例题选讲
D - 刻录光盘
最开始,你可能想当然地直接猜测,只有处于一个强连通分量中的人,才能只发一张光盘,因此只需要求强连通分量的个数就可以了。
然而,这样求出来的个数是比真实答案大的。为什么呢?因为发光盘不需要每个人相互之间都能拷贝,只要从某一个“根”出发能按有向图遍历到所有人,就可以了。那显然一群只要一张光盘的人可以不是强联通分量。
那怎么办呢。我们依然先求出所有强连通分量,并对应记录好每个节点 \(u\) 在强连通分量 \(bel_u\)(\(bel\) 是 belong 的缩写)中。接着,我们根据原图的存储信息,把每个强连通分量视作一个节点,计算出每个强连通分量的入度。
算了入度有什么用呢?这一群人可以是一堆强连通分量串在一起的,如果某个强连通分量可以从另外一个强连通分量拷贝过来,那它自己就不必新领一张光盘了;但是如果没地方给你拷贝,你就得自己新建一个。
那么代码也很好写了。
int main(){
n=read();
for(int x=1;x<=n;x++){
int y=read();
while(y)g[x].pb(y),y=read();
}for(int i=1;i<=n;i++)if(!id[i])Tarjan(i);
for(int u=1;u<=n;u++)for(int v:g[u])
du[bel[v]]+=(bel[u]!=bel[v]);
for(int i=1;i<=tot;i++)if(!du[i])Ans++;
cout<<Ans<<"\n";
return 0;
}
E - 间谍网络
该题与 D 题十分类似。不同的是,D 题可以给任何人光盘,但这题中只有一部分人愿意被收买,而且收买还有价格。
由于收买的时候,只要收买的是那个入度为 \(0\) 的强连通分量中的人,任意一个都是可以的,那么我们在记录每个强连通分量的情况的时候,还要顺带求出该强连通分量中愿意被收买的那些人的价格的最小值。
那么无解是怎么判断的呢。显然,跑 Tarjan 时经过过的点最终一定是能被掌控的,那经过过的点一定存储了 \(id\) 值(即 dfn 中的对应编号)。而如果某个点没有存储,那显然是无法被掌控的了,这时回答无解并输出该人编号即可。
实现上有一些细节:
- 要将无法被收买的人的收买价格初始化为 \(\infty\)。
- 从某个人最初进入 Tarjan 遍历时,不是每个人都能进去遍历,只有能被收买的人才能进得去。
void Tarjan(int u){
f[u]=(++cnt),id[u]=f[u];
st.push(u),vis[u]=1;
for(int v:g[u])
if(!id[v])Tarjan(v),f[u]=min(f[u],f[v]);
else if(vis[v])f[u]=min(f[u],id[v]);
if(f[u]==id[u]){
vector<int> tmp;
tmp.clear();mn[u]=a[u];
while(tmp.empty()||tmp.back()!=u)
vis[st.top()]=0,tmp.pb(st.top()),
bel[st.top()]=u,mn[u]=min(mn[u],a[st.top()]),st.pop();
SCCs[++tot]=tmp,hav[tot]=u;
}return;
}
int main(){
n=read(),p=read();
for(int i=1;i<=n;i++)a[i]=0x3f3f3f3f;
for(int i=1;i<=p;i++){int x=read();a[x]=read();}
m=read();
for(int i=1;i<=m;i++){
int x=read(),y=read();
g[x].pb(y);
}for(int i=1;i<=n;i++)
if(!id[i]&&a[i]!=0x3f3f3f3f)Tarjan(i);
for(int i=1;i<=n;i++)if(!id[i])
{cout<<"NO\n"<<i<<"\n";return 0;}
for(int u=1;u<=n;u++)for(int v:g[u])
du[bel[v]]+=(bel[u]!=bel[v]);
for(int i=1;i<=tot;i++)
if(!du[hav[i]])Ans+=mn[hav[i]];
cout<<"YES\n"<<Ans<<"\n";
return 0;
}
F - Cow Ski Area G
最开始的连边和建图是简单的,不过需要把二维点坐标转化为一维的位置信息值。依然是跑 Tarjan,从每个没被经过过的点出发跑 Tarjan。
但是问题来了,有多少个位置需要建缆车呢?首先特判全图连通不需要建缆车直接输出 \(0\),否则,我们统计入度和出度分别为 \(0\) 的强连通分量个数,取 \(\max\)。
为什么呢,我们首先看入度为 \(0\) 的,那说明其他地方进不来这里,那肯定得修个缆车;而出度为 \(0\) 的,那说明无法出去到其他地方,也肯定得修个缆车。而只需要选择其中更完整的一种做到底就可以让全图连通了,故取 \(\max\)。
void Tarjan(int u){
f[u]=(++cnt),id[u]=f[u];
st.push(u),vis[u]=1;
for(int v:g[u])
if(!id[v])Tarjan(v),f[u]=min(f[u],f[v]);
else if(vis[v])f[u]=min(f[u],id[v]);
if(f[u]==id[u]){
vector<int> tmp;
tmp.clear();++tot;
while(tmp.empty()||tmp.back()!=u)
vis[st.top()]=0,tmp.pb(st.top()),
bel[st.top()]=tot,st.pop();
SCCs[tot]=tmp;
}return;
}
int Num(int x,int y){return (x-1)*L+y;}
int main(){
L=read(),W=read(),n=W*L;
for(int i=1;i<=W;i++)
for(int j=1;j<=L;j++)wg[i][j]=read();
for(int x=1;x<=W;x++)
for(int y=1;y<=L;y++)
for(int k=0;k<4;k++){
int x2=x+dx[k],y2=y+dy[k];
if(x2<1||x2>W||y2<1||y2>L)continue;
if(wg[x2][y2]>wg[x][y])continue;
g[Num(x,y)].pb(Num(x2,y2));
}
for(int i=1;i<=n;i++)if(!id[i])Tarjan(i);
for(int u=1;u<=n;u++)for(int v:g[u])
if(bel[u]!=bel[v])du[bel[v]]++,ot[bel[u]]++;
for(int i=1;i<=tot;i++)Ans+=(!du[i]),res+=(!ot[i]);
if(tot==1)cout<<"0\n";
else cout<<max(Ans,res)<<"\n";
return 0;
}
G - 校园网 Network of Schools
我们发现第一问的答案就是 D 题,求入度为 \(0\) 的强连通分量个数。于是把代码 copy 过来即可。
接着我们发现,第二问的答案就是 F 题,求入度为 \(0\) 和出度为 \(0\) 的强连通分量个数的 \(\max\),甚至不需要二维转一维。于是继续把代码 copy 过来即可。
然后就做完了,代码懒得贴,直接去看我 D 和 F 的,毕竟我做的时候也是 copy 的。
简单总结
强连通分量,即 SCC,指在有向图中的极大强连通分量,有 Tarjan 算法可以在 \(O(n+m)\) 的时间下求出一张 \(n\) 个点 \(m\) 条边的有向图的所有强连通分量的具体情况。其经常运用在图中求连通性或求连通块个数等,也会加以变形出题。这里有两个相对较常用的结论,也是上面的例题中用到过的结论:
- 给定一张有向图,若要求计算至少要选定几个起点才能跑遍全图,则答案是整个图中入度为 \(0\) 的强连通分量个数。
- 给定一张有向图,若要求计算至少需要加上几条有向边才能让全图强连通,则答案是整个图中入度为 \(0\) 和出度为 \(0\) 的强连通分量个数的 \(\max\) 值。
还有更多有关强连通分量的结论,在此不一一叙述。还有些题目会让你进行图论建模,本来是与图无关的题面,但是经过些许转换后可以变成图论的题目。总之,强连通分量是在有向图中运用极多的内容,Tarjan 也是求强连通分量的一大好工具,是非常棒的算法喔!
Thanks reading.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号