学习笔记 差分树状数组
在四月份还在自由校区的时候,Lbmttw_lx中午不远千里的来到清华,来听David_alwal大佬讲解树状数组,当时被这个优美的lowbit函数震惊了,与这个优美的函数相对应的,还有这个优秀的时间复杂度,可以在log级别的时间复杂度里做出区间修改和区间查询的工作

首先我们来回顾一下普通的树状数组,就是可以单点修改和取件查询的那一种qwq
代码分为三个部分,第一个部分,就是著名的lowbit函数
1 int lowbit(int x) 2 { 3 return x&(-x); 4 }

这个lowbit操作主要是利用二进制,来计算的
lowbit(x&(-x)):返回二进制最低位1的值:比如x=1010那么lowbit值为2。
x+lowbit(x):把最后一位二进制最低位1,往前进一位。
x-lowbit(x):去掉最后一位二进制最低位1。
我们认为凡是x+lowbit(x)代表父亲节点,x-lowbit(x)代表儿子节点。
然后是我们的update操作(我的函数名比较毒瘤)
inline void add(int x,int y) { for(res int i=x;i<=n;i+=lowbit(i)) { c[i]+=y; } }

最后就是我们的区间查询了(这个只能查询1-n的前缀和,我们需要在最后输出的时候输出ask(r)-ask(l-1))
1 int ask(int l) 2 { 3 int ans=0; 4 for(int i=l;i;i-=lowbit(i)) 5 { 6 ans+=l*c[i]-sum[i]; 7 } 8 return ans; 9 }
回顾的差不多了吧,是不是很简单呢
正文分割线
首先,我们在OI中常常会遇到这样的问题,给定一个区间,需要对这个区间内的每一个数字都加上或者减去一个特定的数,我们的朴素算法的时间复杂度是O(n)的,但是常规的题目中一般对时间复杂度的要求都非常的严格,这样的时间复杂度显然是我们无法忍受的,所以我们怎么办呢?引入一个升级版的数据结构——差分树状数组!可以log级别内实现区间修改

首先,什么叫做差分呢?
定义数组c[i]=a[i]-a[i-1],数组c即为差分数组

(图片引自https://www.cnblogs.com/bluefly-hrbust/)
所以,根据上述的结论,我们在区间修改和查询的时候只需要维护两个变量就可以了,一个是差分数组c[i],和一个b[i](求c[i]*(i-1)的)
好的,那么我们来看单点修改的操作
C[i]还是与原来的树状数组一样更新,c[i]+x即可
b[i]=c[i]*(i-1)那么b[i]=(c[i]+x)*(i-1)即b[i]=(c[i])*(i-1)+x*(i-1)我们更新x*(i-1)即可
更新效果:把x位置后面所有的数的值+w
1 inline void add(int x,int y) 2 { 3 for(res int i=x;i<=n;i+=lowbit(i)) 4 { 5 c[i]+=y; 6 sum[i]+=y*(x-1); 7 } 8 }
然后是区间查询
只需要在原有的代码上加上
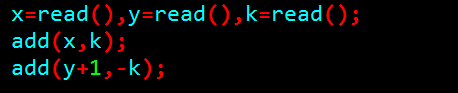
效果:在[x,y]的区间上每个数都加上K,很显然是吧
然后区间查询上文以及说过了,不再赘述。
代码如下

1 #include <bits/stdc++.h> 2 #define MAXN 100050 3 #define res register 4 #define db double 5 #define standard 1e-5 6 #define ll long long 7 using namespace std; 8 int c[MAXN],a[MAXN],n,m,x,y,k,sum[MAXN]; 9 int lowbit(int x) 10 { 11 return x&(-x); 12 } 13 inline void add(int x,int y) 14 { 15 for(res int i=x;i<=n;i+=lowbit(i)) 16 { 17 c[i]+=y; 18 sum[i]+=y*(x-1); 19 } 20 } 21 int ask(int l) 22 { 23 int ans=0; 24 for(int i=l;i;i-=lowbit(i)) 25 { 26 ans+=l*c[i]-sum[i]; 27 } 28 return ans; 29 } 30 ll read() 31 { 32 int s=0,w=1;char ch=getchar(); 33 while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} 34 while(ch>='0'&&ch<='9'){s=(s<<1)+(s<<3)+ch-48;ch=getchar();} 35 return s*w; 36 } 37 int main() 38 { 39 n=read(),m=read(); 40 for(res int i=1;i<=n;i++) 41 { 42 a[i]=read(); 43 add(i,a[i]-a[i-1]); 44 } 45 for(res int i=1;i<=m;i++) 46 { 47 int s; 48 s=read(); 49 if(s==1) 50 { 51 x=read(),y=read(),k=read(); 52 add(x,k); 53 add(y+1,-k); 54 } 55 else 56 { 57 x=read();y=read(); 58 int ans=ask(y)-ask(x-1); 59 printf("%d\n",ans); 60 } 61 } 62 return 0; 63 }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号