学习笔记 康拓展开及其逆运算

刷到NOIP基础4，看到火星人那道题，以为需要用逆康拓展开，当时就慌了，结果看下数据范围就安心了，直接用next_permutation解决了

 

之后看到康拓展开的模板题，以为next_permutation加上深搜也能过，结果开O2优化也超时很多...

 

在被Th_Au_K奆老嘲讽后，Lbmttw_lx就要开始苦逼的学习康拓了

 

之前模拟赛有一道题就是康拓展开，以为多么难，就没做23333

进入正题分割线——————————————————————————————————————————————————————————————————

 

1.康拓展开

 

首先呢，康拓展开是一个处理全排列问题的...公式（算是吧）

 

用法是，给定一个全排列，求其字典序（正用），或者给定字典序，求全排列（逆用）

 

在OI中的用途：


1.获取全排列id，构建哈希表，充当哈希函数（不知道哈希函数和哈希表的同学看上一条博客）

 

2.求解全排列序列的字典序，求解模板类问题（如NOIP 2004 火星人）

 

全排列的定义大家都知道吧，在这里不在赘述了

 

给大家一个样例，感受一下

 

已知n=3，求2 1 3 在全排列中的字典序

 

解法1：看到这个的时候，第一想法就是用STL函数，next_permutation

 

从1 2 3开始循环next_permutation，直到达到目标，break，记下此时循环了多少次，字典序就是多少

 

分析：这样做的好处是非常简单，思路很好想，但是时间复杂度过高，next_permutation的平均时间复杂度为O（n），而我们的全排列一共有n！中，也就是说我们的总时间复杂度是O（n！*n），这显然在信息学竞赛中是不可取的，数据一旦超过11，就直接爆炸。

 

那么有没有更好的办法取缔next_permutation函数呢？显然是有的，今天的主角康拓展开就可以登场了

 

解法2：康拓展开处理

 

我们已知的全排列是2 1 3，也就是第一位为2，当第一位为1的时候，比当前的全排列小，所以一共有1*2！种方案比当前方案小

 

第二位为1，没有比当前排列更小的方案了，所以是0*1！

 

第三位为3，因为2和1在之前的数位中已经用过了，所以当前数位只有一种方案，即没有比当前排列更小的方案了

 

我们作和，一共有2种全排列要比当前的排列小，所以，当前排列的字典序是3

 

根据数学归纳法，我们可以得到康拓展开的公式

 

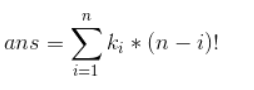
其中k[i]表示对于第i位的a[i]，a[i+1]到a[n]种比a[i]小的数字的个数

 

由理论，我们可以很轻松的写出康拓展开的代码

 

 1     for(int i=1;i<=n;i++)
 2     fac[i]=fac[i-1]*i;
 3     ll ans=1;
 4     for(int i=1;i<=n;i++) 
 5     cin>>a[i];
 6     for(int i=1;i<=n;i++)
 7     {
 8         ll k=0;
 9         for(int j=i+1;j<=n;j++) 
10         if(a[j]<a[i]) 
11         k++;
12         ans+=k*fac[n-i];
13     }
14     cout<<ans<<endl;
View Code

 

分析：我们这种做法的时间复杂度可以无限接近于常数了（因为OI中关于全排列问题的数据范围都很小），相比于next_permutation要优很多。

 

 

 

2.逆康拓展开

 

样例：已知n=3，求字典序为3的全排列

 

同样可以用next_permutation求解，不过时间复杂度过高

 

逆康拓展开求解过程：

 

我们需要求解字典序为3的全排列，也就是说有3-1=2个全排列要比所求全排列字典序小

 

从第一位开始考虑：2/!2=1，也就是说第一位有1个数字比所求全排列小，所以第一位是2

 

2-2！=0，也就是说，第二位没有数字比所求全排列小，所以第二位是1

 

由于2和1在之前的数位已经用过了，所以第三位只能是3

 

得出，字典序为3的全排列是2 1 3

 

我们可以很轻松的写出代码

 

 1 void recarton()
 2 {
 3     bool vis[200050];
 4     memset(vis,0,sizeof(vis)); 
 5     fac[0]=1;
 6     m--; 
 7     int q,j,cnt; 
 8     for(int i=1;i<=n;i++){
 9         q=m/fac[n-i];
10         m=m%fac[n-i];
11         cnt=0;
12         for(j=1;;j++)
13         {
14             if(!vis[j]) 
15             cnt++;
16             if(cnt>q) 
17             break;
18         }
19         a[i]=j;
20         vis[j]=true;
21     }
22     for(int i=1;i<=n;i++) 
23     cout<<a[i]<<" ";
24     cout<<endl;
25 
26 }
View Code

 

上OJ上那道例题

题目描述

输入两个自然数m，n期中1<=n<20,1<=m<=n!，输出给定的排列在n个数全排列中按小到大第几个出现？输出n个数全排列中第m种全排列。

输入

第一行两个整数n，m；
接下来一行n个数，n个数的一种排列。

输出

第一行一个整数，表示给定排列是全排列中第几个。
第二行输出n个数全排列中第m个全排列。每两个数之间空一格。

样例输入

3 2
1 2 3

样例输出

1
1 3 2

 

代码如下：

 1 #include <bits/stdc++.h>
 2 #define ll unsigned long long 
 3 #define mo 998244353998244353
 4 using namespace std;
 5 ll n,m,a[200050],b[200050],cat[20];
 6 ll k=1;
 7 bool vis[200050]={0};
 8 void contor()
 9 {
10     for(int i=1;i<=n;i++)
11     {
12         ll ans=0;
13         for(int j=i+1;j<=n;j++)
14         {
15             if(a[j]<a[i])
16             ans++;
17         }
18         k+=ans*cat[n-i];
19     }
20 }
21 void recontor()
22 {
23     m--;
24     int t,j,point;
25     for(int i=1;i<=n;i++)
26     {
27         int fac=n-i;
28         t=m/cat[fac];
29         m=m%cat[fac];
30         point=0;
31         for(j=1;;j++)
32         {
33             if(!vis[j])
34             {
35                 point++;
36             }
37             if(point>t)
38             {        
39                 break;            
40             }
41         }
42         b[i]=j;
43         vis[j]=1;
44     }
45 }
46 int main()
47 {
48     cin>>n;
49     cin>>m;
50     for(register int i=1;i<=n;i++)
51     {
52         scanf("%d",&a[i]);
53     }    
54     cat[0]=1;
55     for(int i=1;i<=25;i++)
56     cat[i]=cat[i-1]*i;
57     contor();
58     cout<<k<<endl;
59     recontor();
60     for(int i=1;i<=n;i++)
61     cout<<b[i]<<" ";
62     return 0;
63 }
View Code

 

 注意一下，做数论的时候一定要注意开long long，十年OI一场空，不开long long见祖宗啊（昨天晚上调1个多小时没好，结果今天改long long A掉？？？） 

 

附上一部分惨图

 

 

posted @ 2019-08-10 14:28  落筱  阅读(289)  评论(0)  编辑  收藏  举报