图形学笔记-Games101
向量
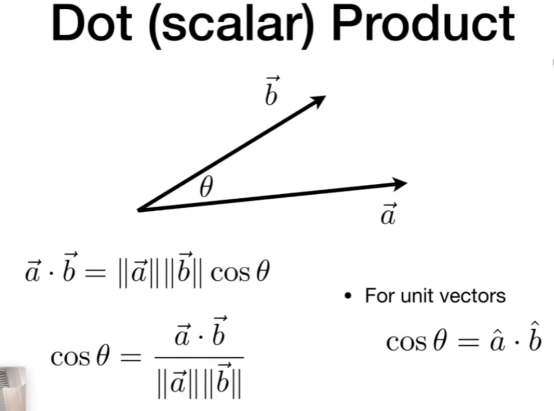
- 点乘。
- 在图形学中一般使用:知道两个向量,算他们的夹角。
- 点乘使用交换律、分配律、结合律
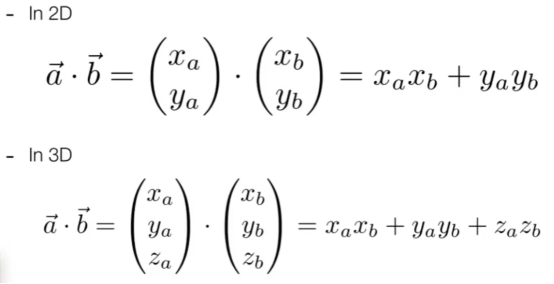
Vector3 a = new Vector(x1, y1, z1);
Vector3 b = new Vector(x2, y2, z2);
//计算对应的余弦值
double cosValue = (a.x1 * b.x2 + a.y1 * b.y2 + a.z1 * b.z2) / a.magnitude * b.magnitude;
// 计算对应的弧度值
double angleInRadians = Math.Acos(cosValue);
// 将弧度转换为角度
double angleInDegrees = angleInRadians * (180 / Math.PI);
- 叉乘。
- 其结果垂直于AB,垂直的方向由右手螺旋法则定义(×前的向量指向×后的向量)。
- 由于括号内的意思的原因,使用不满足交换律,交换后需加上负号
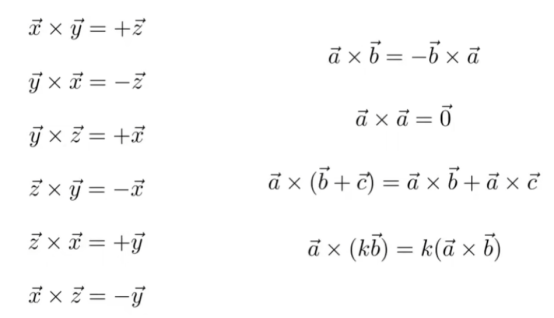
-
向量叉乘自己是零向量;满足结合律和交换律
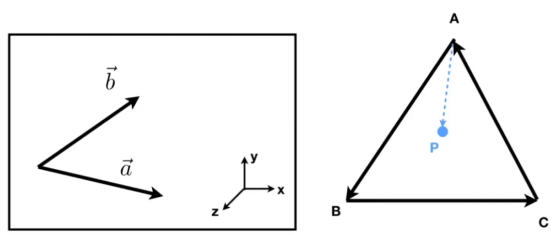
- 用于判断b在a的左侧还是右侧。
- 用于判断P在△ABC的内侧还是外侧(AP在AB的左,BP在BC的左,CP在CA的左)。
查看代码
Vector3 CrossProductResult(Vector3 origin, Vector3 point1, Vector3 point2){ Vector3 sideA = point1 - origin; Vector3 sideB = point2 - origin; // 使用叉乘计算平面的法线向量 return Vector3.Cross(sideA, sideB).normalized; } bool IsPointInTriangle(Vector3 pointA, Vector3 pointB, Vector3 pointC, Vector3 target){ Vector3 cross1 = CrossProductResult(pointA, pointB, target); Vector3 cross2 = CrossProductResult(pointB, pointC, target); Vector3 cross3 = CrossProductResult(pointC, pointA, target); return cross1 == cross2 && cross2 == cross3; }
矩阵

- 矩阵:AB矩阵相乘只有符合A矩阵的列等于B矩阵的行才能乘。
-
相乘结果怎么出来的:在结果里看他的行/列,去A的行和B的列找所有数字,把这些数字点乘起来就行了。
-
如:如何得出(二行,三列)的61,找到A的二行5/2,找到B的三列9/8,点乘5*9+2*8。

-
矩阵不存在交互律,但是其他的都能用。

-
转置。
OpenGL一般使用列项
Unity和UE使用行项
你问我什么是列项什么是行项?
问GPT。
Transform
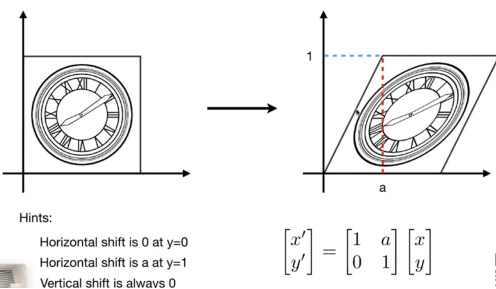
- 切变:
[x + ay]
[y]
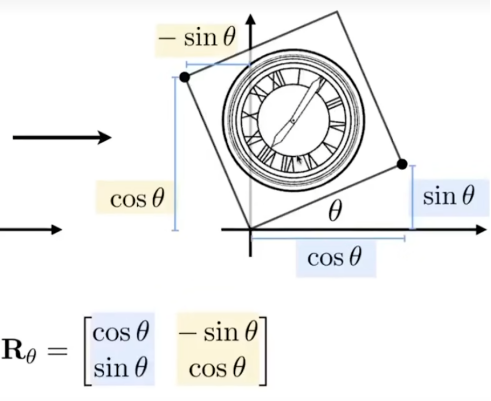
- 二维旋转

- “三元数”官方:齐次坐标
- 其中,出现了新的概念,点和向量的区别。

- 在引入w之后,w=0表示向量,w=1表示点
- v(x1,y1,0)+v(x2,y2,0)=v(x1+2,y1+2,0);
- p(x1,x2,1)-(x2,x2,1)=v(x,y,0);
- p(x1,x2,1)+v(x2,y2,0)=p
- 点加点则引入了一个新概念,新产生的点为相加两点的中点(w==2)


- 先旋转还是先平移->产生的结果不一样。
- 此图表示先旋转,再平移。

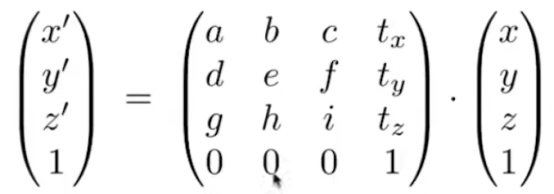
- 四元数。
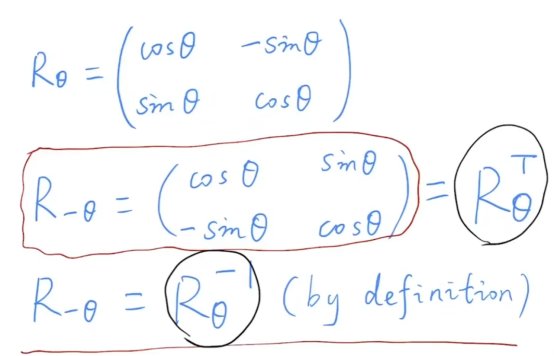
- 负角度(矩阵的逆)写来出之后发现等于矩阵的转置(官方:正交矩阵)
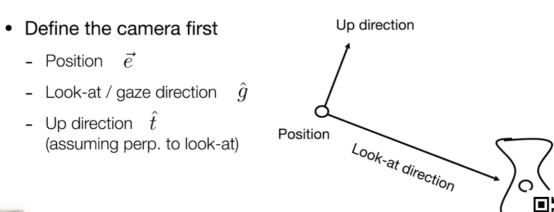
- 如何定义一个视角:位置、朝向、上方向
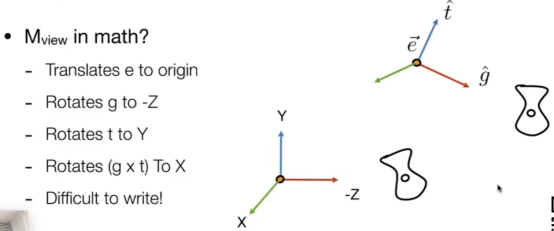
- 目标:将右上角的摄像机放到左下角的原点、且方向一致。
- 如图。
- 那么该如何写步骤呢?
- 自然是把e移至原点;
- 从t/g改为-z/y的旋转矩阵一般情况下写不出来,因此使用逆↓
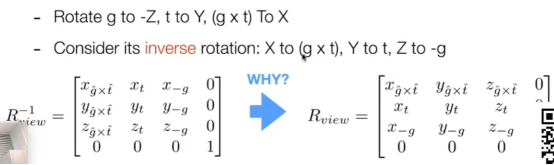
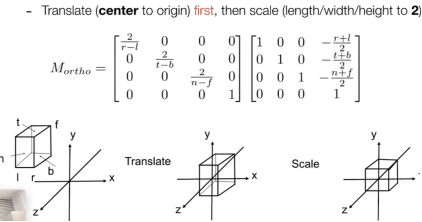
- 正交-矩阵:把任意地方的矩形变成原点±2的正方体
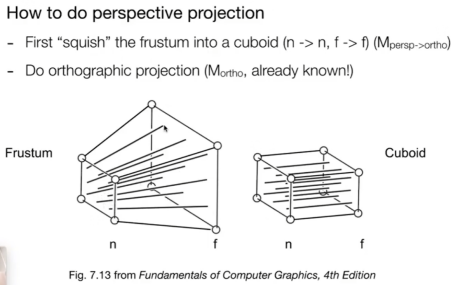
把左边‘f’的面压缩,变成右边的‘f’,任意点的矩阵怎么写呢
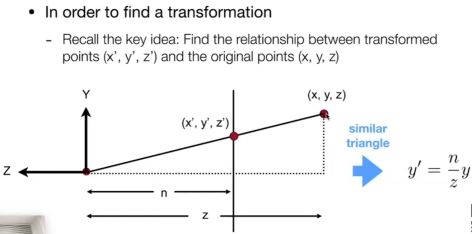
- 首先:比例是n/z,于是我们就得出了下图

- 其次:我们根据z不变的原则,把远面f的z乘上n/z

- 然后我们就知道了(00 ??)那么怎么求AB呢?
- 使用了远面f中点不会改变的例子,n符合,f也符合


- 于是:对远面的“挤”所需要的矩阵就完成了,把远面乘以这个矩阵就得到了挤压后的面。然后再用正交的方法成像就可以了。
光栅化

- Raster(光栅):俄语,屏幕的意思
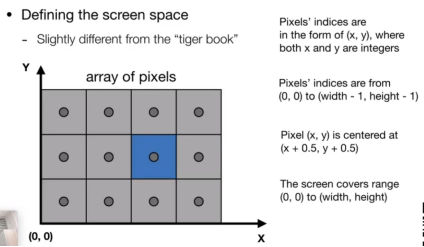
- 定义:左下角方块为(0,0),其中心是(0.5,0.5);蓝色方块为(2,1),其中心为(2.5,1.5)

- 视口变换
-
先不管Z;把XY的[-1,1]变成[0,width]x[0,height]使用的是如图矩阵;拉长->平移。
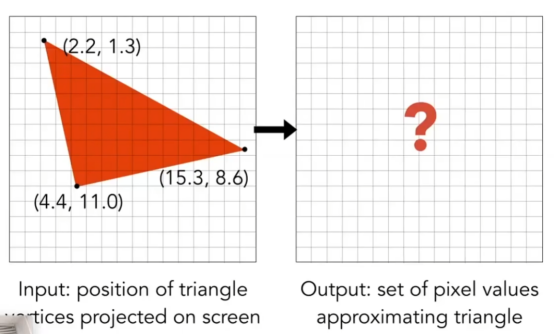
- 场景中模型都是由一个个三角形拼出来的,那么在‘挤’->‘挤之后的矩形变成正交矩形’->视口变换之后,必定在屏幕上有一个三角形。
- 但是屏幕是由一个个像素组成的,三角形穿过这个像素的大小有大有小,那咋办呢?

- 如图,这方面的定义是采样。采样:给你一个函数f(x),你用x=1,2,3...去问f(x),是多少,f(x)给你的值就是采样后的答案;就是把函数离散了,就只拿点。
- 显存在拿到图片之后,去每个像素的中心找值,后面就不用说了。
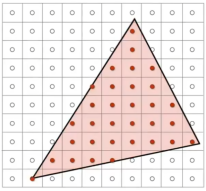
就这个。
- 那么该如何判断这个点是否在三角形内呢?做叉乘
- 边界处理:自行定义。
- 问题,会有锯齿问题的出现。
反走样(抗锯齿)和深度缓冲
- Artifact:锯齿、手机拍电脑的摩尔纹、车轮倒转现象等。翻译叫瑕疵,但不绝对。
- 原因:信号变化太快,导致采样频率跟不上。
- 操作:模糊。

- 原理层面:傅里叶变换。
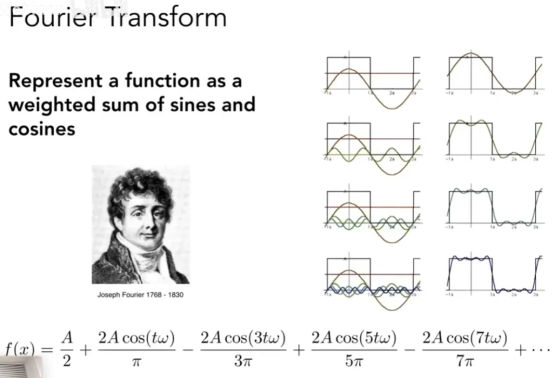
- 傅里叶级数展开


- 把低频的地方删去,只留下高频的部分↑ ↓同理

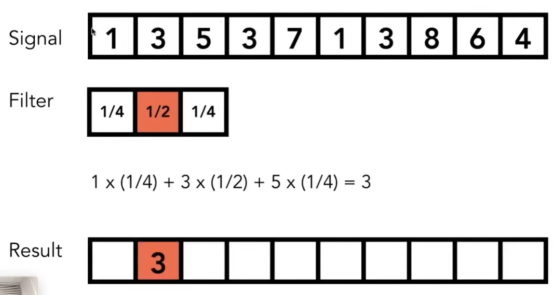
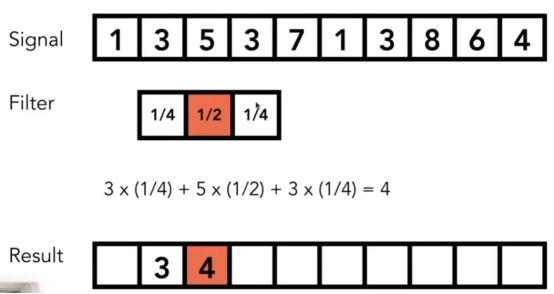
- 卷积:取平均数。在原始的数据,取周围数的平均。(模糊用)*图形学上的简化操作。

- 时域上:卷积。频域上:傅里叶变换。
- 说一下个人理解吧:就是没理解。大致意思应该是通过傅里叶变换可以得到模糊的边界,然后就可以减少锯齿。
- 但是计算机层面我看懂了:把一个像素分成n*n个点,求这n2个点的RGB平均值,然后再赋值给这个像素,最后就得到了模糊的边界。

- MSAA(专有名词)
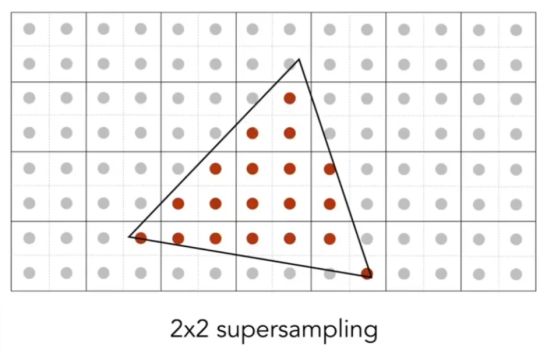
- 把一个像素分成2x2个点。
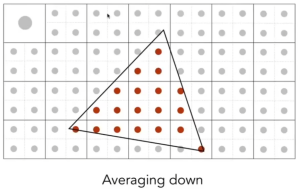
- 求平均:第一个点
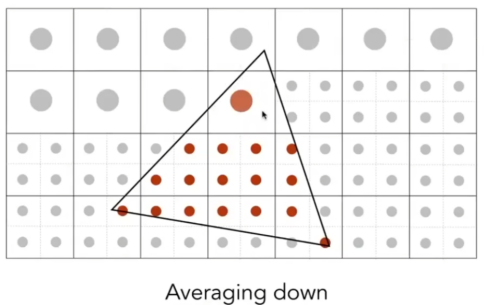
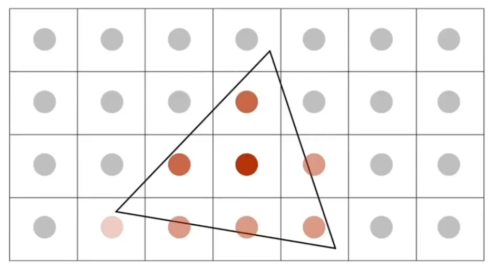
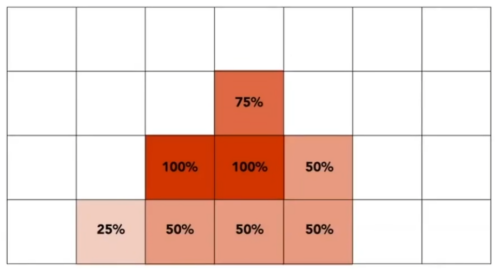
- 懂了吗。
Shading
- 有一种渲染方法是从远处开始渲染:画家渲染法,先画山,再画树再画人。应用到计算机里就是先渲染远处的三角形,再渲染近处的三角形,但是这一做法具有较大的局限性。
- 比如遇上这种情况
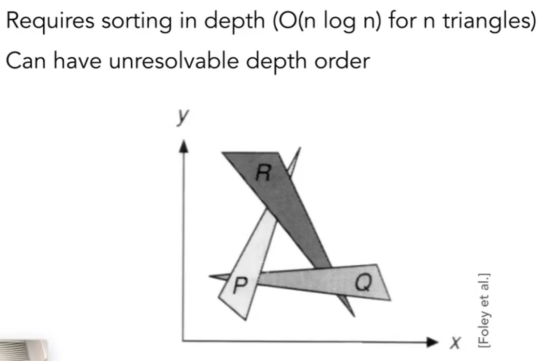
- 使用通常使用像素渲染法:Z-Buffer。
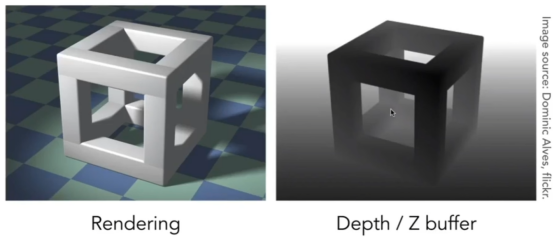
- 先通过算法得到深度图,然后才进行渲染。

- 解析:一开始,每个像素所对应的点都是无限远的地方,然后一层层向视角走,如果有三角形,就拿三角形所对应的点RGB值和深度(depth)z。
- 然后继续靠近视角,倘若在这个过程中,之前赋值过的像素点的z,有更小的z可以替代了,那么就更新这个z值。
- 思路如图。
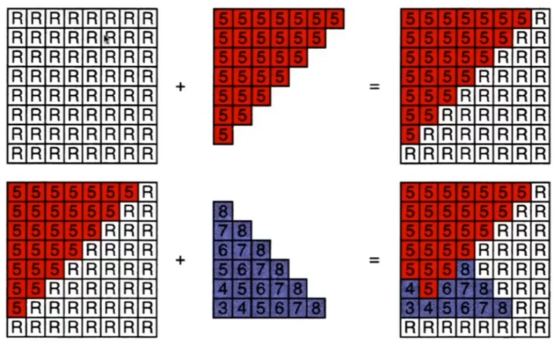
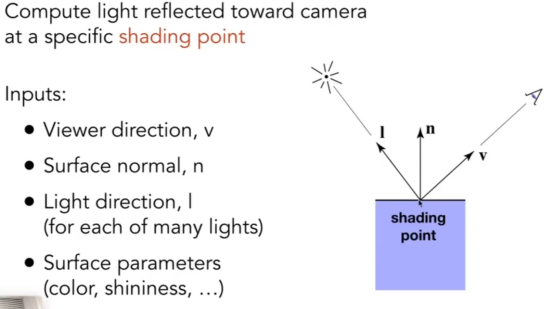
- 视角看到的颜色和以上数值有关:观察方向V、法线方向n、光照方向l,还有shadingpoint。
- 都是单位向量:这样就可以控制视角可看到的物体的材质,是金属或是木头。
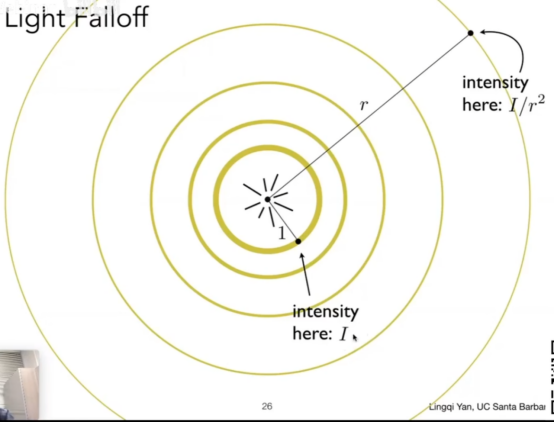
-
一个点光源,半径越小,单位面积上的能量就越大,设半径为r,光照强度为I,那么右上角那个点的强度(intensity)就是I/r方。
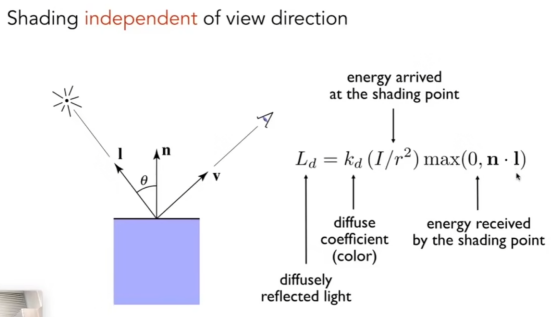
- 通过这个公式就可以拿到某个点的漫反射光照强度。
- L:漫反射;k:反射强度系数;(使用max是不考虑折射情况)
- 因为是漫反射,所以每个方向上观察到的颜色都是一样的,因此跟v没有关系。

- 讲完了漫反射,来讲镜面反射,虽然有镜面一词但不是镜面,镜面反射是出射角处的高光,
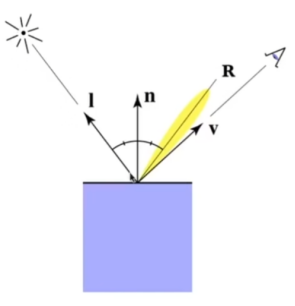
计算R和v的差,可以得出高光项。
- 但是呢,布林和模型:引入了半程向量h(v和l的中心向量),这样就不需要去计算出射角R,只需要计算h,再用h和n做一下点乘,就可以求出高光项,计算优化。
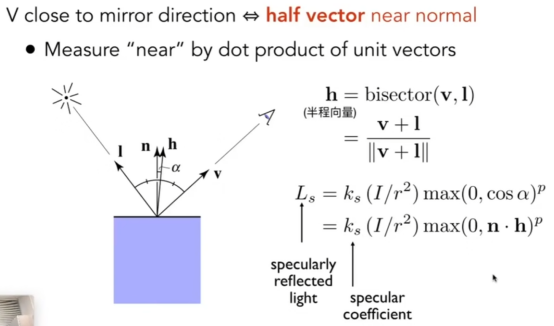
- 其次,为什么右上角有个p呢:如图,点乘后得出的值比较大,n和h相差89度也很大,因此给它一个指数,如p=64,那这样就只能在20°左右才能看见高光。(p一般100-200)
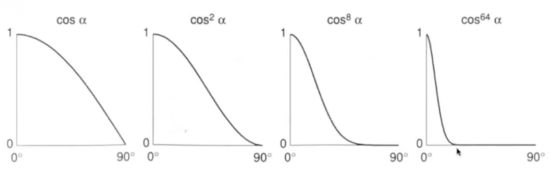
- 结果:


- 环境光照:光在经过一次又一次的漫反射和反射后,会打到物体背光处,从而把物体背光处打亮,但是现实显然不可以去计算如此复杂且多的光照。
- 因此我们假设每一个点都受到相同的环境光照强度:

- 于是我们就得到如图,环境光+漫反射+高光=布林和反射

- 着色频率。
- 平面着色:取每个面的中心点进行着色,会得到如图的模型。

- 高罗德着色(点着色)

- 得到三角形顶点的颜色(假设法线能求)然后在三角形内部,三个点之间的平面颜色使用三个点的插值来计算,得到如图。
- phong着色,获得两个相邻三角形的法线,利用插值计算其间每个像素的法线,再依次相加计算每个反射光。

- phong着色,获得两个相邻三角形的法线,利用插值计算其间每个像素的法线,再依次相加计算每个反射光。
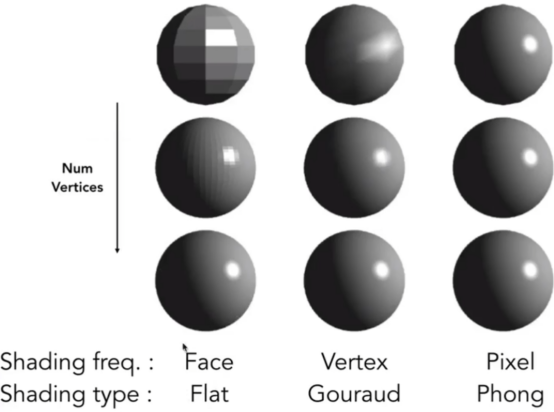
- 着色频率越高就越不用高级着色法。
渲染管线
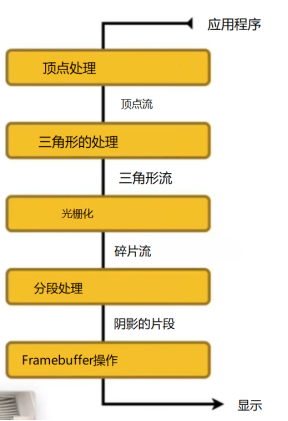
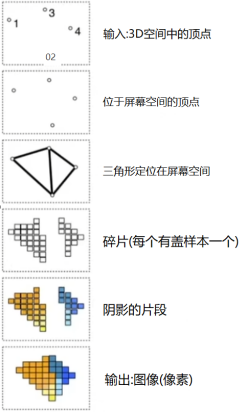
1. **应用程序阶段(Application Stage)**:此阶段由应用程序负责设置场景、相机和物体属性等信息,并将数据传递给图形API(如OpenGL或DirectX)。
2. **几何阶段(Geometry Stage)**:首先,几何阶段通过顶点着色器(Vertex Shader)对每个顶点进行变换和处理,将其从模型空间转换到裁剪空间。接下来,进行剔除(Culling)、裁剪(Clipping)和透视除法(Perspective Division)等操作,最终得到屏幕空间的顶点坐标。
3. **光栅化阶段(Rasterization Stage)**:在这个阶段,根据裁剪后的三角形片元(Fragment)的屏幕位置,生成覆盖像素的片元。这些片元会被进一步处理以确定它们在屏幕上的最终颜色。
4. **片元处理阶段(Fragment Processing Stage)**:在这个阶段,通过片元着色器(Fragment Shader)对每个片元进行处理。片元着色器可以使用纹理、光照等信息计算最终的颜色。
5. **光栅化操作阶段(Raster Operations Stage)**:在这个阶段,进行深度测试(Depth Testing)、模板测试(Stencil Testing)和混合(Blending)等操作,以确定哪些片元应该被渲染到最终的帧缓冲区。
6. **输出阶段(Output Stage)**:最后,将最终生成的图像从帧缓冲区输出到屏幕上进行显示。
- 也就是说,除了顶点和片元处理,其他的操作都是一样的。
- 所以在现代计算机中,显卡都帮你写好了顶点和片元处理之外的操作。
- 我只需要写个顶点和片元处理就行了,即Shader。
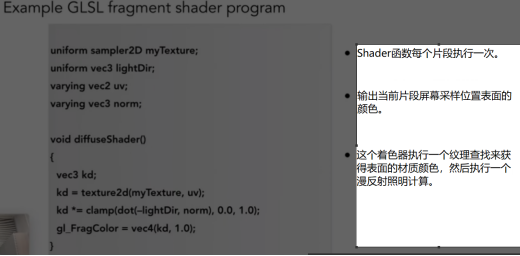
- 上图为片段(像素)着色器。此着色器对每一个像素进行一次漫反射操作。

- 贴图Texture,uv,取值都是0-1.
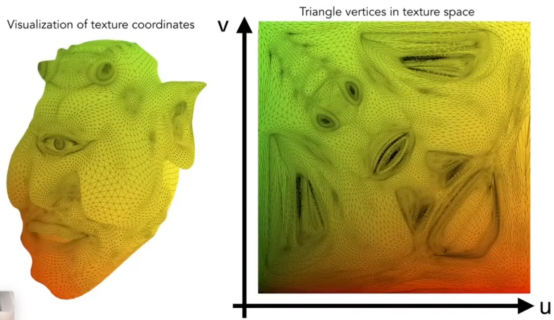
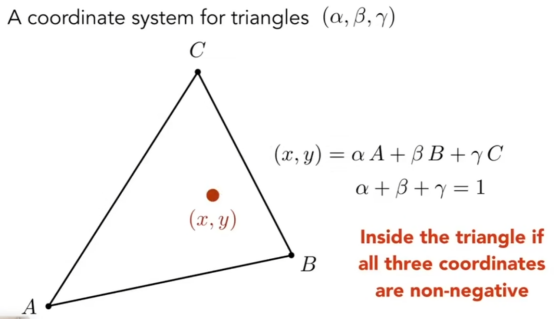
- 重心坐标:任意三角形内的任意一点都可以用α、β、γ去乘ABC这三个点俩表示(系数相加等于一)
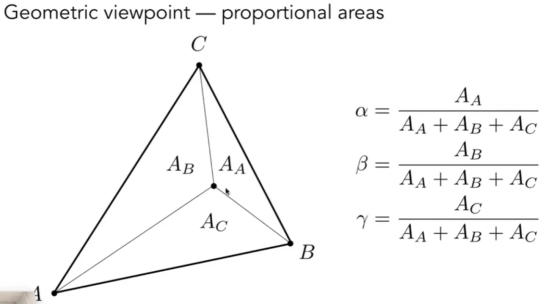
- 系数可以通过面积去求
- 之所以引入重心坐标,是为了对三维空间中,这个三角形的某个点进行插值,以此来计算这个点的颜色。
- 之前说过。把三角形投影到2D屏幕之后再做插值,其实这是不对的。当我们把这个三维的三角形,投影到屏幕上时,重心坐标的位置会发生改变,因此在三维空间中先插值了,在投影,才是正确做法。

- 当一个192*108的图片,想要显示在1920*1080的屏幕上时;
- 首先,我们进行定义:texel是指贴图上的一个像素。
- 那在进行展示的时候,屏幕上的一整块的许多像素仅对应一个texel。
- 这种做法就导致了上图左边图的效果,而这显然不是我们想要的效果。、
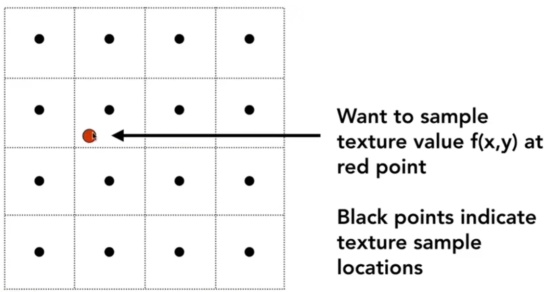
- 因此我们利用了插值的做法。
- 首先,上图中,黑点代表texel,红点应该是密密麻麻的,此图表示的只是其中一个。
- Nearest做法就是把离红点最近的texel给它。
- 插值做法则是取周围四个点:
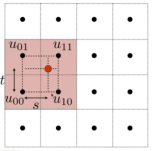
- 双线性插值Bilinear:通过t和s的运算,得到颜色
- 上图做法是取2*2的texel,仔细观察上眼皮,还是有一定的锯齿状。
- Bicubic就是取4*4来插值计算。
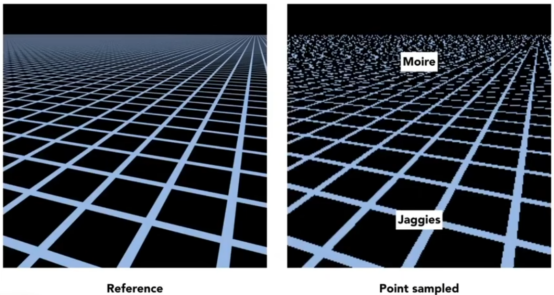
- 相反的,贴图太大,屏幕太小,反而会出现更严重的情况,远处摩尔纹,近处锯齿。
- 于是,我们就使用范围查询,一个屏幕像素对应这很多texel。
- 通过计算这一屏幕像素内所有texel的平均值,来表示这个像素的颜色。
- 特点:很快、会有错误、只能在一个正方形里采样。

- 示例图,MinMap。
- D=log2 X,X表示Level,每一个贴图都会有一个MinMap,原图是Level0,其他的和原图一起存在,虽然有额外7个等级,但是开销非常小,所占用的内存不会超过原图的三分之一。

- 如上图,远处蓝色部分和近处红色部分用的是同一张贴图,但是他们使用的MinMap的层数不一样,根据屏幕两个像素之间的距离L来找贴图之间的距离L,L越大层数就越大。
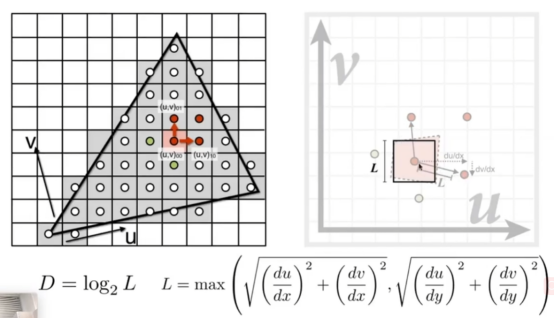
- 在正方形区域,取大一点的L的长度来做一个矩形,这个矩形内的texel的平均值就是MinMap的某个Level。
纹理部分
- 环境光纹理:物体在场景中,一定会受到环境光的影响,然后将自身受到的环境光反射到视角里。
- 其根本是一张贴图,有两种技术:矩形变球体、正方体变球体。

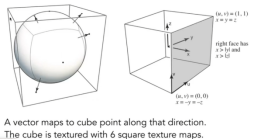

- 凹凸贴图:此贴图通过,改变着色时法线的值来达到凹凸不平的阴影效果。

- 如下图:凹凸贴图在扰动物体表面的法线。
- 计算步骤:我们先假设原始的法线竖直向上,再通过凹凸的十分接近的两点来计算改点的切线的斜率dp,然后就得到了切线向量(1,dp),此切线就是该点的平面,然后可以通过交换x和y来拿到垂直于该平面的法线(-dp,1)。
- 归一化
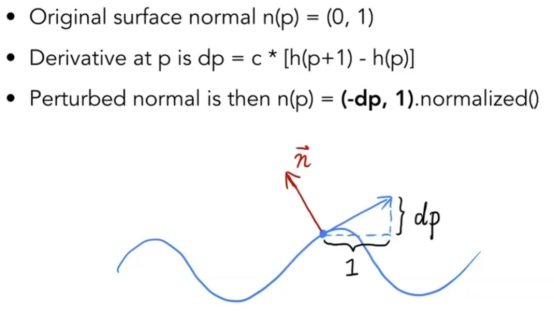
- 3D版也是类似的,只不过变成了uv方向。


- 如上图,此种做法会有缺陷,只是某块地方黑了点,只能简单的骗骗人。
- 因此我们引入了新的技术:使用相同贴图,不同的技术,可以到达非常好的效果
- 此技术名为位移贴图,他通过上下移动该点,来真的在物体表面创建凹凸的效果,这样,物体凸起来的部分,也能给旁边的一些地方创造阴影。
- 但既然要上下移动某个点,就势必会产生更多的技术,同时也需要更多的三角形。
- 现在只有在微软平台能自动划分三角形。
- 同时,贴图不止有2D的,3D的也有。
几何
- 现实生活中,纤维,细胞,等,都非常难用三角形表示出来。
- 因此,有了隐式表达和显示表达。
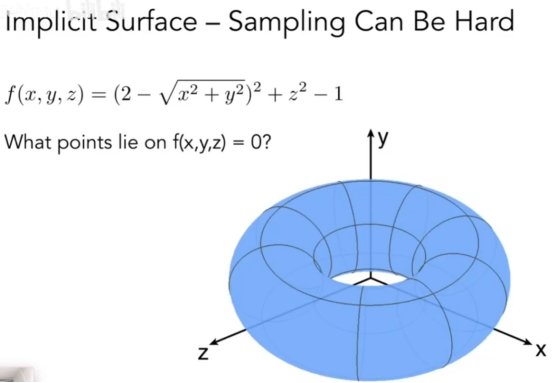
- 上图就是隐式表达,符合fx的所有点就是一个圆环,但是光看表达式看不出来是什么形状。
- 隐式表示-优点和缺点
- 优点:
- 紧凑描述(例如,一个函数)
- 某些查询很容易(内部对象,到表面的距离)(大于或小于零在形状外面)
- 有利于射线到表面的交集
- 对于简单的形状,准确的描述/没有抽样误差.易于处理拓扑的更改(例如,流体)
- 缺点:
- 难以建模复杂的形状
- 因此,隐式表达的都是一些基础模型,在很多建模软件里的那种,通过一个个基础模型的拼拼凑凑和blend(混合),就可得到需要的形状。

- 这是一个Cube的obj文本文件,v代表8个点,vt代表12个纹理坐标,vn代表6根法线(有8个是因为有很多冗余的地方),f内的参数表示(v/vt/vn)
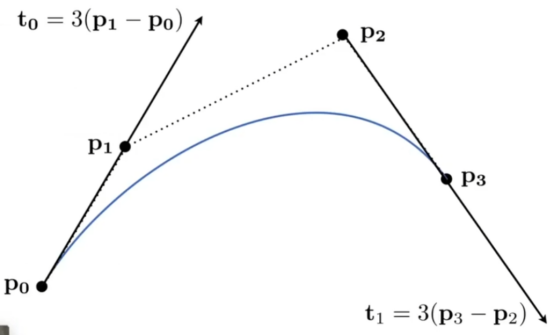
- 贝塞尔曲线
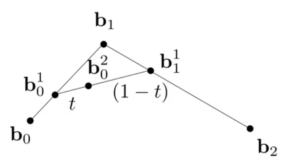
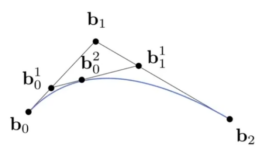
- 三个点,点点之间,去其距离的t倍,得到两个点,这两个点之间距离的t倍,得到一个点。
- 取不同的t,可以得到一条曲线。
- 如下图,四个点也是一样的。
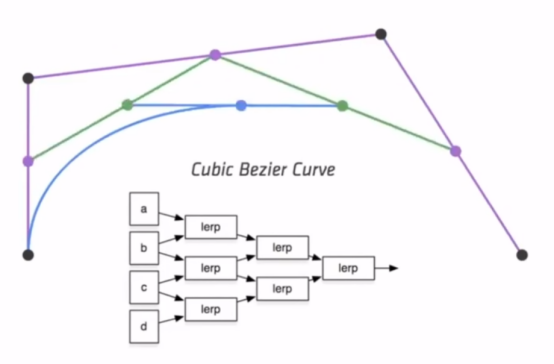
- 既然有t,又有点,那么就可以得到一个公式,如下图。
- 我没去记,很好理解。

- 既然有贝塞尔曲线,那么把二维的线,应用到三维的空间中,也是很容易的。
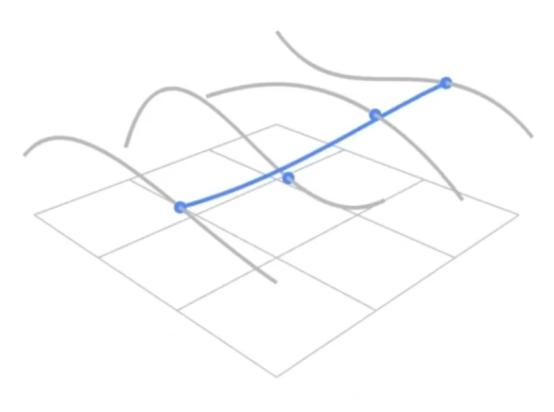
- 得到四条曲线,取同一垂直方向上的四个点,作为新的点,用这新的四个点再来画一条贝塞尔曲线。
- 通过移动这个垂直,就可以得到一个贝塞尔曲面。
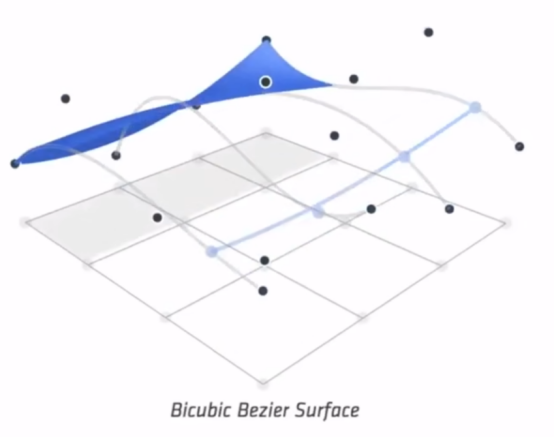
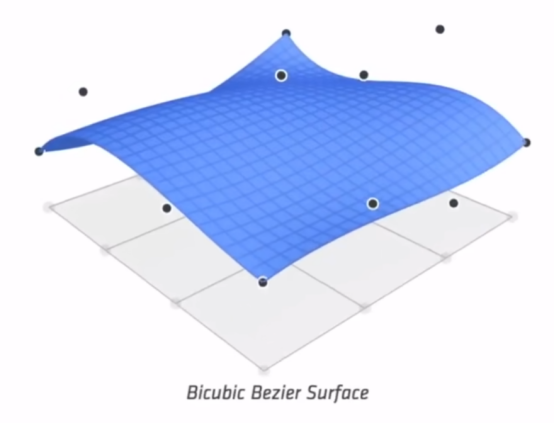
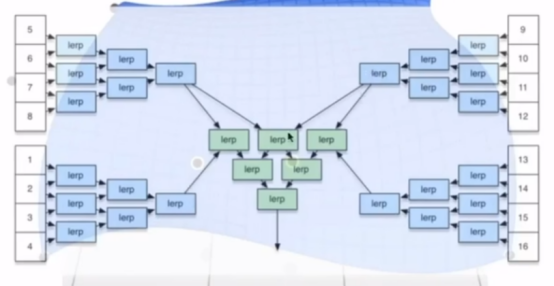
- 和二维算法同根。
- 虽然曲面成像效果非常优秀,但是市面上大部分还是用的网格。

- 网格细分(图2变成图3)
- 网格简化(图3变成图2)
- 网格规划(让模型更正规化,图4的三角形长短大小不一,进行规划之后变成图5,这可以让模型拥有更多不错的性质)
细分
1.loop细分(发明它的人姓loop)

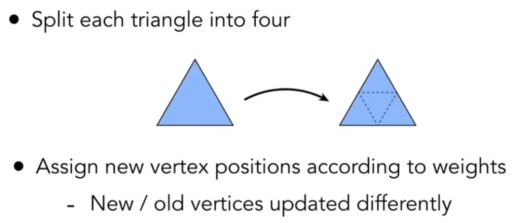
- 取周围几个值的平均,作为新的点
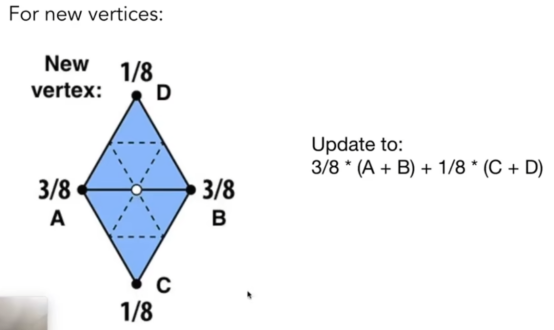
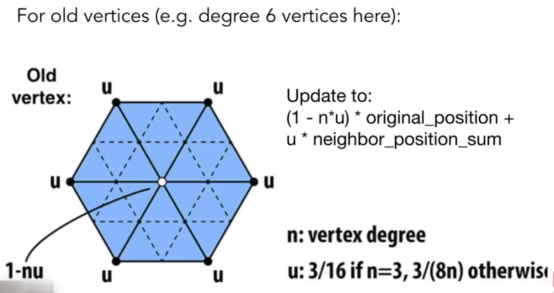
- 先产生新的顶点,根据它的度n(点连着几根线)来决定他是怎么个平均法。
- 得到了新的点之后,原来的u点再根据新的一圈n点来计算(右下角那行)。
- Catmull-Clark细分
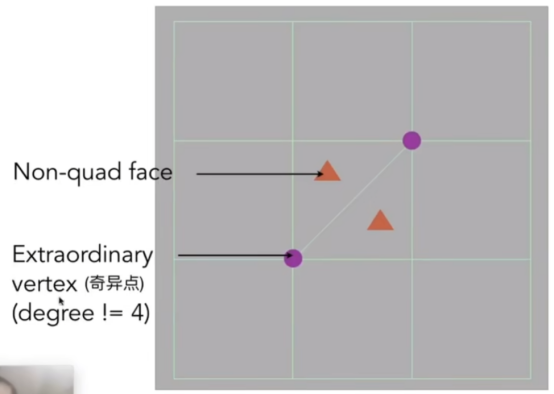
- 如上图:三角形表示非矩形的面(只要不是四条边就算)。
- 紫点表示奇异点:度(和点相接的线)不为4
- 找到这些面和点
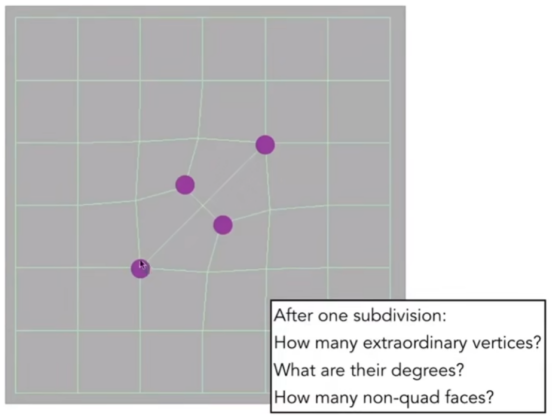
- 将每一条边的中点和非四边形面的重心点,两两相连,得到新的形状
- 这个时候重心点就可能会变成奇异点,先不管点的偏移。
- 有多少奇异点?之前的重心点都变成了奇异点,增加了2个。
- 奇异点的度?变换前的奇异点的度不变,新增的奇异点的度和其边数有关。
- 多少个非四边面?0(很神奇是不是,不愧是图灵奖获得者想出来的方法)
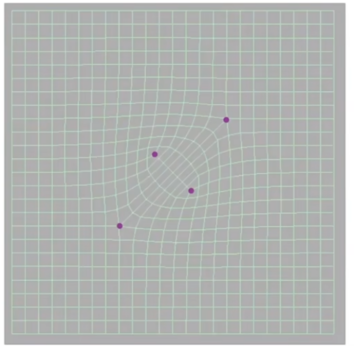
- 再怎么细分也不会增加新的非四边形面或是奇异点

- 计算步骤如图;
- 先算面中点,再算线中点(这两个中点都是四个数的平均)
- 最后调整原先的点,其系数都是研究后得到的结果。
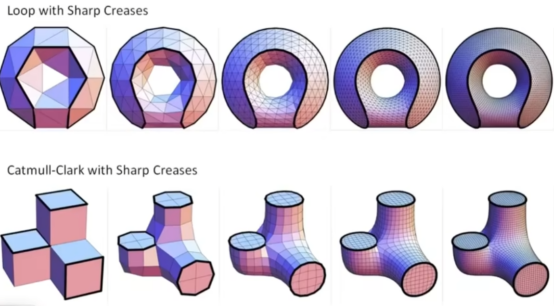
- 如图。
简化:
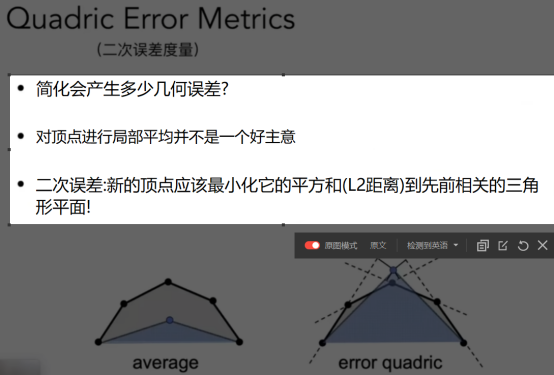
- 取平均不是好方法,因此使用二次误差。
- 原因是因为使用平均,会让这个原本很凸起的面,变得很扁,所以得让它凸。
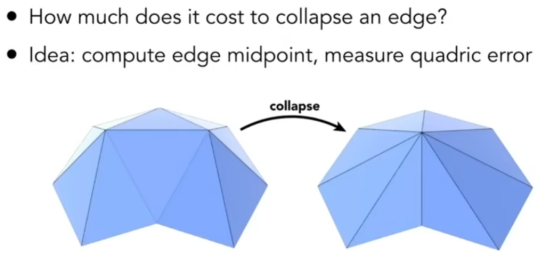
- 如上图,在合并点之后,里我最近的两条边。本来是差不多垂直于我,但是在合并之后和我成差不多45°,这个就是一个误差,称为f。
- 在简化模型时,算法会获得整个模型所有的f,进行一个排序,同时,在简化一次之后,出现了新的f,利用堆的性质,把这个新的f塞进堆里面,重新排序之后再合并最小的f。
光追
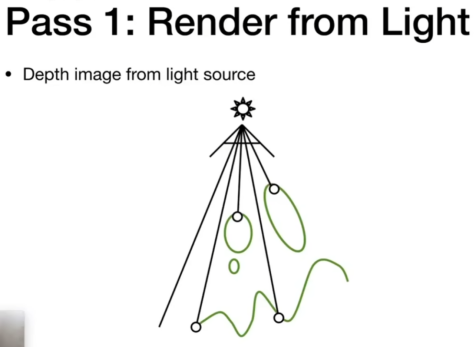
- 阴影制作:适用于点光源
- 原理:光能看到的地方就是亮的。
- 步骤1,在光源处放一个摄像机,拿到深度图。(记录了该点)
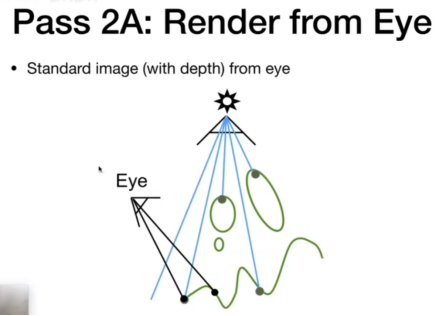
- 步骤2,相机看过去,下图,下面相机投射过去,左边的黑点为例,将此点投射到光源,对比步骤1拿到的深度图,看看该点是不是和深度图上是同一个点,如果是,就打亮,如果不是,就只使用漫反射。
- 显然,左边的黑点就是深度图上的点,因此打亮;右边的点投射到深度图,发现不是,因为有更近的点。
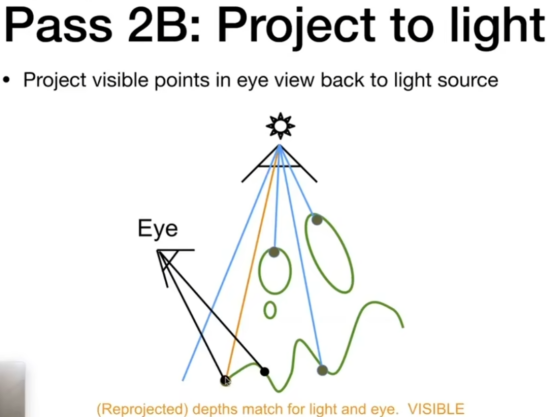
- 如上图:将肉眼可见的点投影回光源。
- 但上述做法有缺点:只能做硬投影,肉眼看到的点,要么亮,要么不亮。

- 硬VS软
- 首先,在开始前,我们先定义光线

- 下图是光追的第一步,和光栅化操作类似。
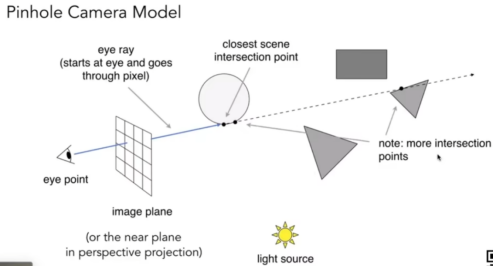
- 下图是第二步,进行反射和折射追踪,计算之后的这些点对观察点的光照影响。
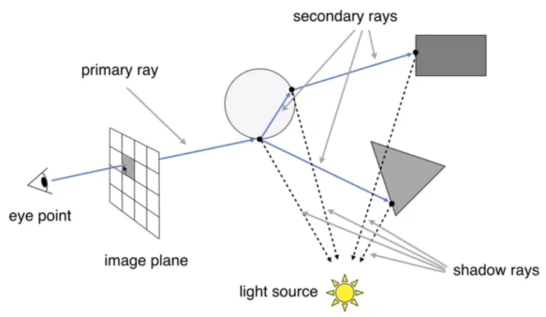
- 计算方面,定义光线:
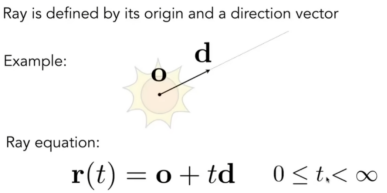
- 定义模型的c和R
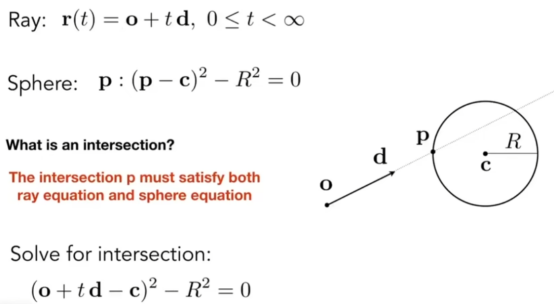
- 我们需要去求t的大小和p是否存在(存在就求)下图易证。
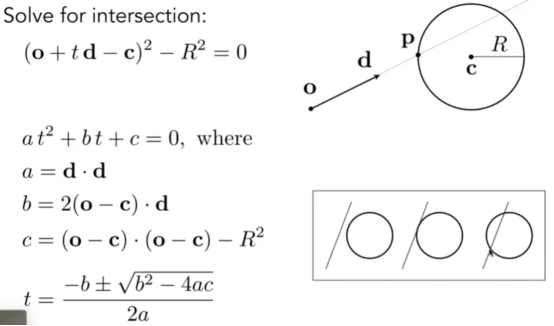
- 点在模型外,与模型必有偶数个交点,在模型内,必有奇数个交点。
- 因此,通过该方法,可以获得隐式模型上所有的点。

- 其次,显式模型方面,我们也进行定义:(下图)

- 通过一根法线和任意一点定义一个面,N和p’,面上面的任意一点p都符合上图公式。
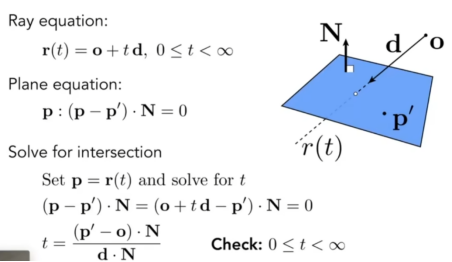
- 于是,我们也得到了t的大小。显式模型也能通过这种方法做出来。还有反射折射。
- 但是这方法虽然真实,但是很慢很慢很慢,一个像素点就要去计算几倍的点。
- 因此我们引入了包围盒模型。

- 上图中的“卷”和“音量”代表包围盒,此处翻译错误
- 也就是射线只需要看看有没有打到包围盒,打到了就去计算,没打到就忽略这个模型的所有面。
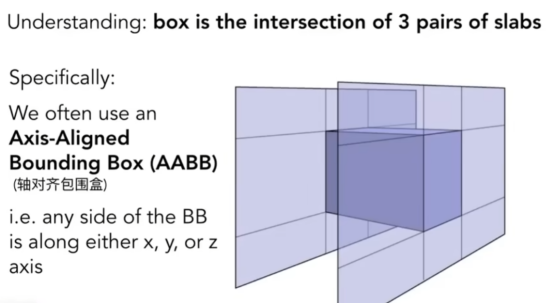
- 使用6个无限延伸的面(两两相对,官方说法是3对面),去包围,其相交的空间就是盒。
- 然后就是去打射线。
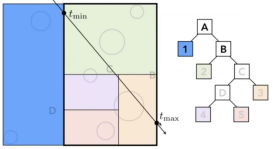
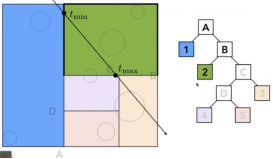
- 如下图,仔细观察左边和中间图的tmin和tmax,这是都是为什么使用3对“对面”的原因,因为这可以再次减少计算,在拿到不同的tmin和tmax后,光线最后进去的tmin和光线最先出来的tmax,就是我们需要的tmin和tmax,如果这两个值不一样,那么就把这个模型算进去。
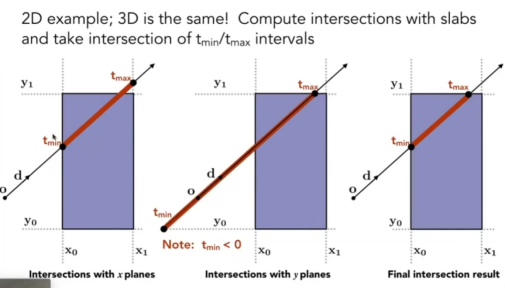
- 该如何去找到这些包围盒,毕竟物体本身是没有这样一个盒子的。
- 方法一:把整个场景用盒子平均分开
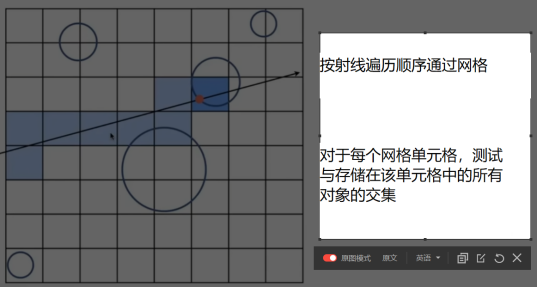
- 通过的网格怎么计算:找到第一个网格,下一个网格只可能是它周围的四个,很好获得。
- 弊端:假如说一个操场中央有一个茶壶,那么平均分的情况下,很多的盒子都是空的,那么为了渲染一个茶壶,要去遍历这么多的空盒子,显然是有优化方案的。(如下图)
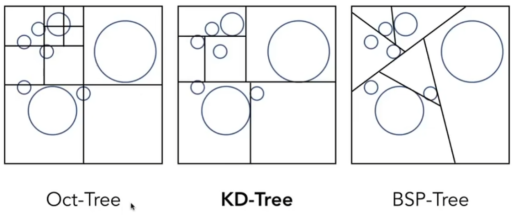
- Oct-Tree是八叉树
- 竖切-横切-竖切-横切......
- 切完之后去盒子中检测物体多不多,多的话再切
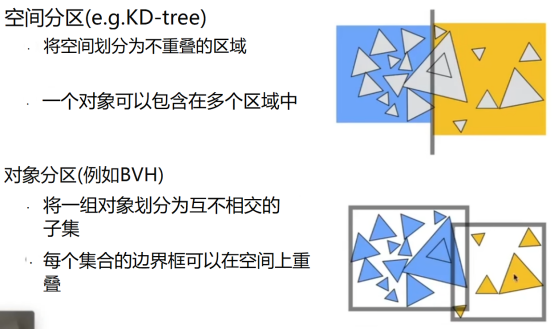
- 弊端:每一个端点上都可能有8个分支,闹;同一个物体存在于多个盒子中。
- KD-Tree是二叉树
- 竖切-横切-竖切-横切......
- 但不是平均切,而是通过其他算法来识别物体,然后再切,最好是把物体分开。
- 这样就只需要计算二叉树。
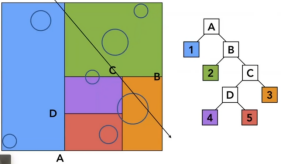
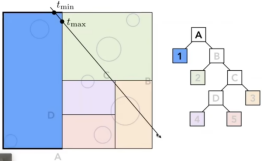

ok就是这样,一个个遍历,特别快。
- 但是弊端还是同一个,同一个物体在不同的盒子中,这样就会造成多余的检测。
- 所以现在市面上用的最多的是下面的,以物体为界来分的包围盒。
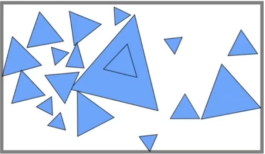
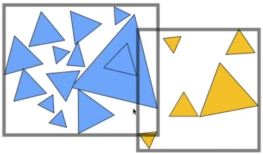
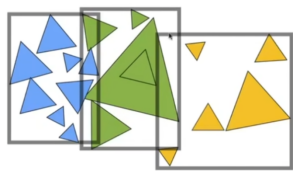
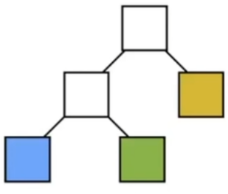
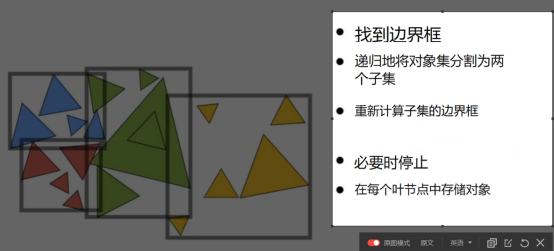
- 伪代码
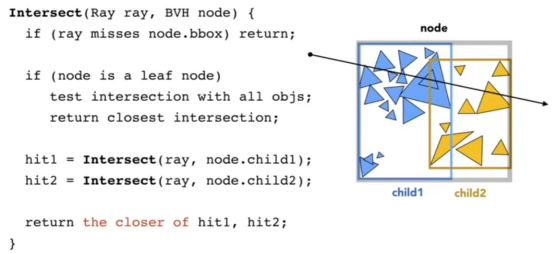
- 详情图
辐射度量学
- 例如在之前学习的光照强度中,我们粗略地把光照强度定义为10,但是这个10是什么,我们没有定义,而这显然是错误的。
- 所以辐射度量学就是带给光线各种物理量,使图形看不出来是加的。
- 声明:本知识点的专业名词尚未有国内翻译,因此都是英文。
- RadiantEnergyand Flux(power)
- 定义:辐射能RadiantEnergy是电磁辐射的能量。单位为焦耳,用符号表示:Q[J/焦]
- 定义:辐射通量RadiantFlux(功率)是单位时间内发射、反射、发射或接收的能量。
- 用白话来说就是亮度
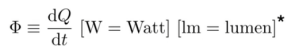
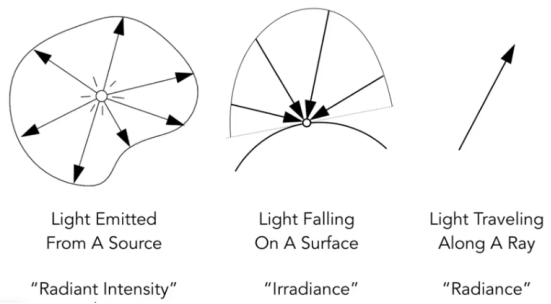
- 光强,吸收光之后反射的光,光线
- 这些是如何运作的。
- Randiant表示单位立体角上光强。

- Irradiance定义:每(垂直/投影)单位面积入射一个表面点的功率。
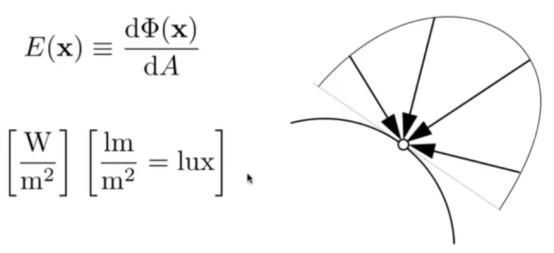
- 上图是明确的概念,下图是简化的模型。
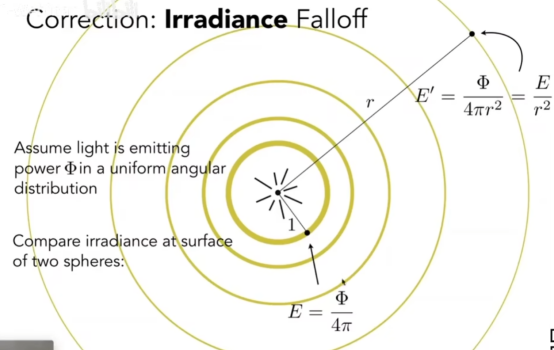
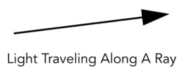
- Radiance是描述光在环境中的分布的基本场量;
- 是与光线相关的量;
- 是计算亮度的;
- 定义:辐射度Radiance(亮度)是一个表面每单位立体角和每投影单位面积发射、反射、透射或接收的功率。
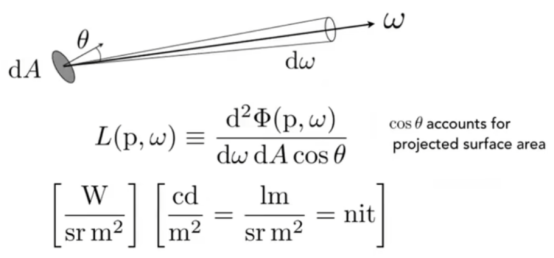

- 如上图所示,Irradionce是单位面积接收或辐射的能量;Intensity是单位立体角辐射的能量。
- Radiance就是单位面积接收了能量之后,再辐射出去的一大块面积中单位立体角的能量
- 同时也是单位立体角辐射出去之后,一大块面积中单位面积接收到的能量。

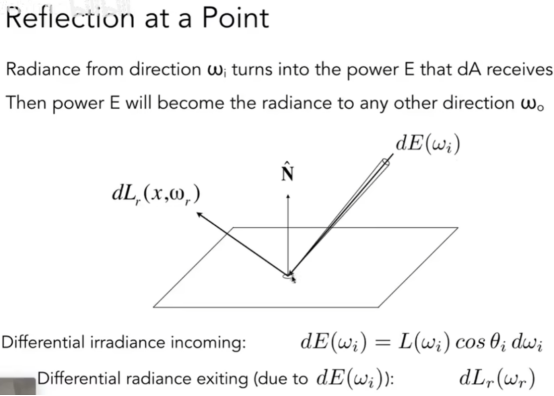
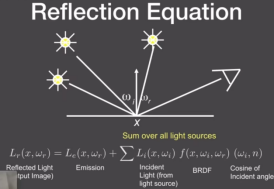
- 双向反射分布函数(BRDF)表示从每个入射方向反射到每个出射方向的光量
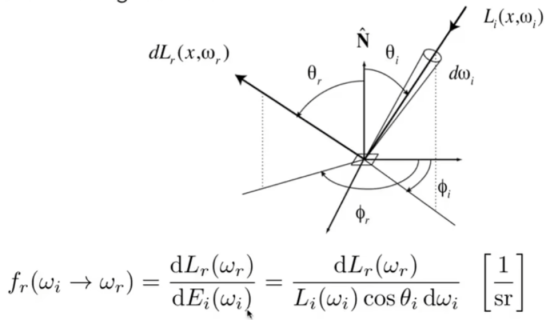
- BRDF会告诉我,该点从某个入射方向进来的光,反射到出射方向,有多强。
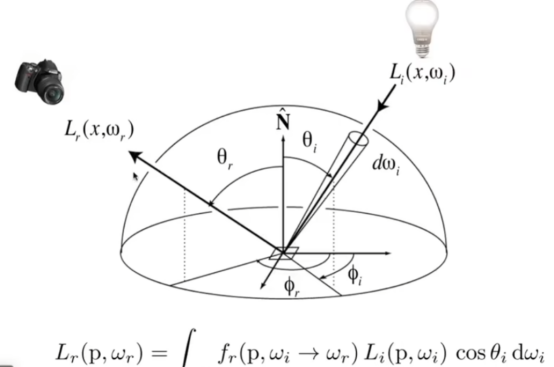
- 是一种递归的算法
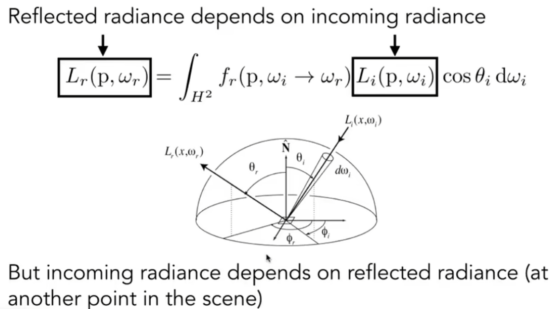
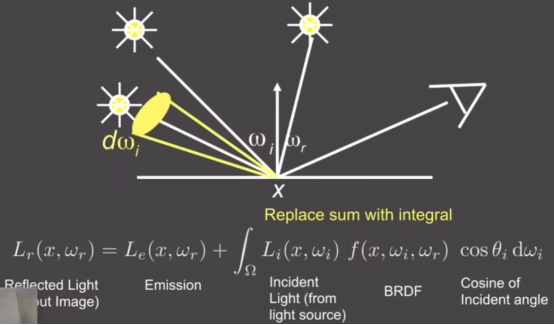
- 物体假如自己会发光,因此,我们添加了一个项来表示物体发的光,于是就得到了最后的渲染方程:

- 通过一个方程,定义所有的光线
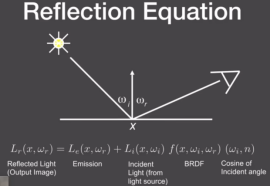
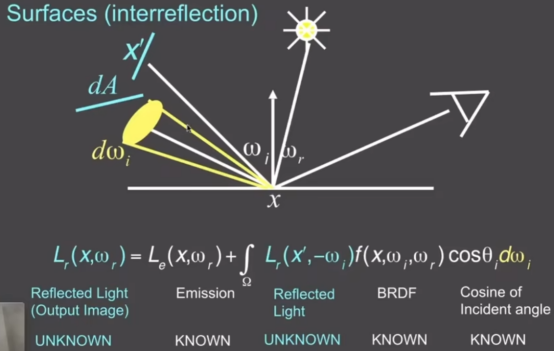


- 场景中所有光线路径的近似集合

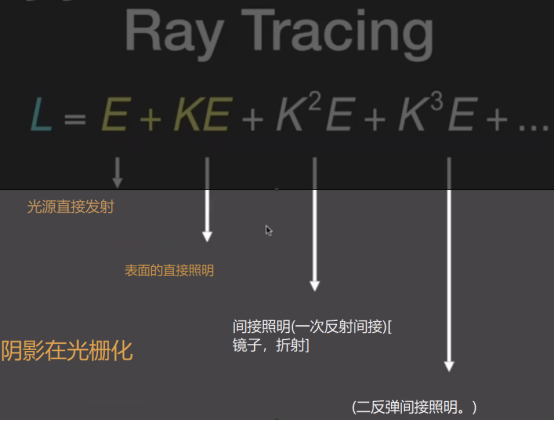
- 牛逼,橙色字就是光栅化,光直接射到屏幕或者弹射一次到屏幕的光。






- 它最后会收敛到某一亮度。
- 蒙特卡洛积分
- 我们想知道一个不规则的积分,使用解析法太难了,以此使用蒙特卡洛积分
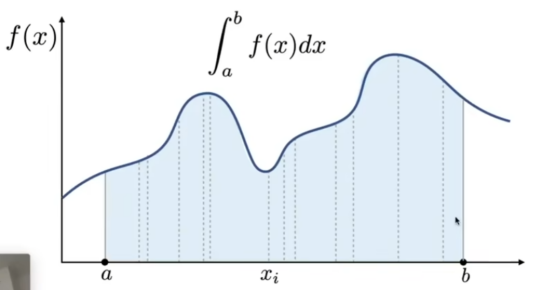
- 在每一个点取它的值,累加起来。通过平均函数值的随机样本来估计函数的积分。
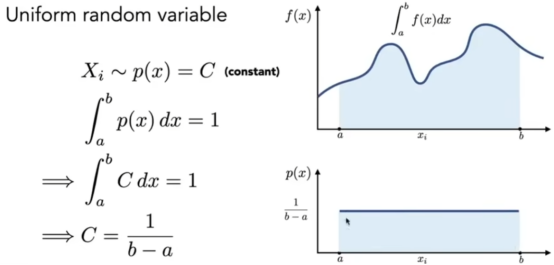
- 如上图,随机到的点x对应的fx为高,b-a为宽,乘起来就是该点的积分,很多的加起来,得到的值除以随机点的个数N,就是本函数的积分,
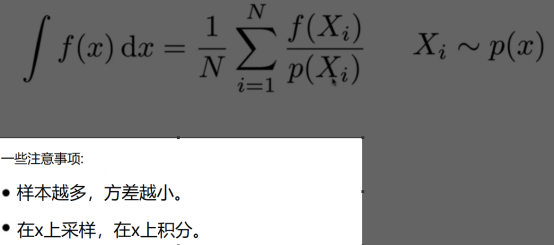
- Whitted-style射线跟踪:
- 总是进行镜面反射/折射
- 停止在扩散表面反弹
- 这些简化合理吗?
高层次:让我们逐步改进Whitted-style的光线跟踪,并引出我们的路径跟踪算法。


- Pathtraced·Whitted-style追踪是错误的·但是渲染方程是正确的·但这涉及到求解整个半球的积分递归执行·如何用数值方法求解积分?
- 假设我们想在下面的场景中渲染一个像素(点),只用于直接照明
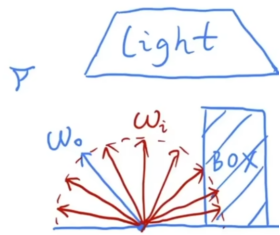
- 我们去每个Wi采样,计算每一次采样得到值,并累加。

- 于是我们就得到了上图代码:在N个样本里随机采样-初始化Lo-对每一个wi进行光先计算,如果这束光打到了光源,就用BRDF去计算。
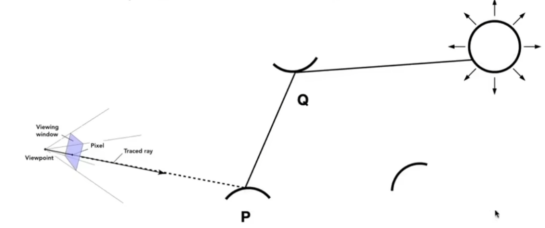
- 那么刚刚算了直接光照,现在来算间接光照。

- 蓝色部分就是答案,倘若这束wi打到了物体,那么在物体上再做一次shade函数计算。
- 但这么做是有问题的:指数爆炸,每次Foreach都要做相同倍计算。
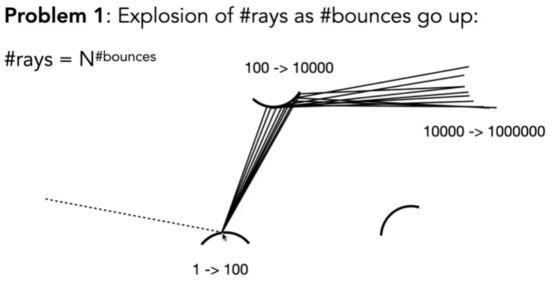
- 因此,我们把上图中的N变成1,也就是说一次只打一条射线,这样会大幅减少计算,我们需要做的是增加采样点。
- 从现在开始,我们总是假设在每个阴影点只追踪1条光线。

- 但这么做会出现很多采样不精准的情况,但问题不大,因为一个像素由场景中很多点组成,让他多做几次光追,最后取个平均就行了。
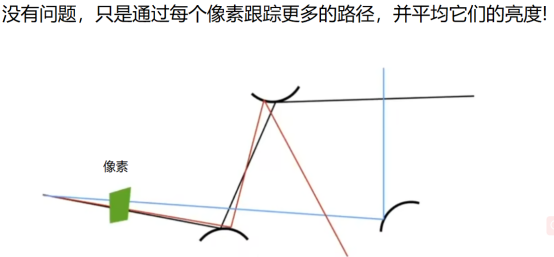
- 下图是像素层面的计算,也是根据蒙特卡洛积分,射出平均射线去进行采样。

- 但是到这,射线还不会停,只要不打到光源他就会一直反射下去,这显然是不对的。
- 因此我们引入了俄罗斯轮盘赌。(下图)

以前,我们总是在阴影点拍摄光线,得到阴影结果Lo
假设我们手动设置一个概率P (O <P< 1)
返回阴影结果除以P: Lo / P
有1-P的概率,如果不发射射线,你会得到0
通过这种方式,您仍然可以期望得到Lo!:
E= P* (Lo / P) + (1 - P) *O = Lo
- 也就是说,通过对期望的计算,我们也可以得到最后的亮度。

- 再说回来,使用了一个点只打一次线的算法下,要怎么运气好,才能打到光源。
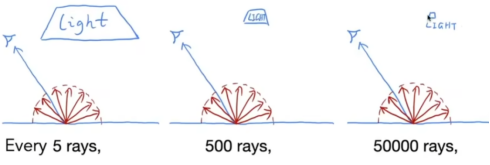
- 光源大->打5条射线线,小,就可能是500/5000条。
- 因此需要进行优化,也就是先去算光源打到该点的线。
- 同一个BRDF,既然可以从摄像机打到光源,那么也可以从光源打到摄像机。
- 需要将渲染方程作为dA的积分需要dw和dA之间的关系。
- 简单!回想一下立体角的另一种定义:在单位球面上的投影面积。
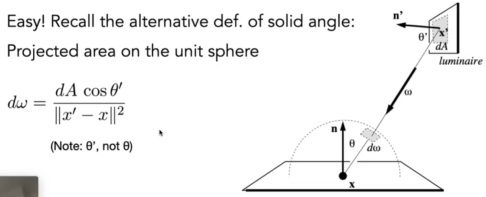
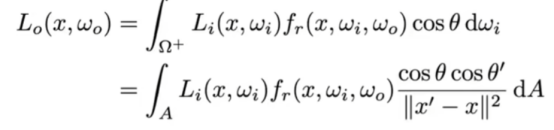
- 就是简单的替换一下就行了。

- 然后在shade函数上的修改就是在反射前先去计算光源方向的光线。
- 之前,我们假设光线是由均匀半球采样“意外”拍摄的(小几率采样到)
现在我们考虑射线来自两个部分:
- 光源(直接,无需用俄罗斯轮盘赌)
- 其他反射器(间接,需要俄罗斯轮盘赌)
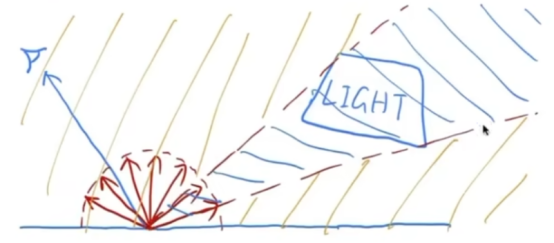
- 最后最后最后一件事:我们怎么知道灯上的样品是否被挡住了?(如下图)
- 我们的做法就是先去检测一下有没有挡住,不被挡到才去算。
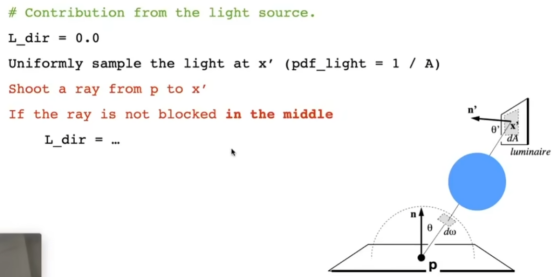
材质
- 物体描述了某一种材质,那么是在渲染方程中的哪一部分决定了物体的材质呢?
- 入射光 BRDFCOS自发光......
- 答案是BRDF,反射不同光的方式。
![]()
- 光在每个输出方向上的反射是相等的。假设入射光均匀:
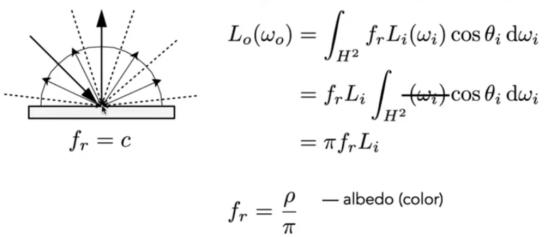
- Fr就是物体颜色。
- 微表面:漫反射是怎么来的,因为物体表面是粗糙的,一束光打到表面上被物体表面一个个小镜子反射到不同方向。
- 粗糙表面
宏观macrosurface:平坦和粗糙
微观microsurface:凹凸不平和镜面
- 表面的个别元素就像镜子一样
被称为Microfacets
每个Microfacet都有自己的标准


- 上述都是各向同性材质,其实在很多金属部件方面,用到的还有各向异性材质(从不同的方向打过去,得到的高光不一样)



渲染中的高级方法
- 无偏光传输法
- 无偏蒙特卡罗技术不存在任何系统误差
- 无偏估计的期望值总是正确的值,不管使用了多少样本
- 否则,有偏
- 一个特殊的情况是,期望值收敛到正确的值,因为使用了无限的#samples – consistent
- 其一:双向路径跟踪(BDPT)
- 路径追踪是从相机到光源
- 追踪摄像机和光线的子路径
- 连接两个子路径的端点。
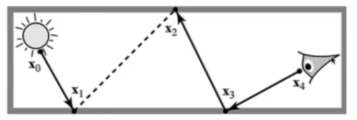
- 当光线传播在光源处比较好计算时,双向路径跟踪(BDPT)效果会很好。
- 但是会慢很多。

- 其二:Metropolis光线传播(MLT)
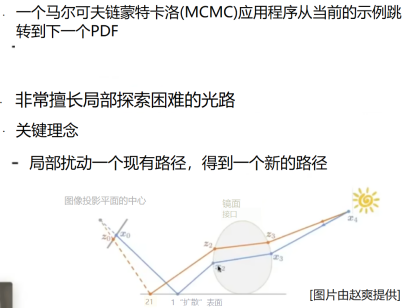
- 如上图所示,MLT在找到一条路之后,会根据这条路,去它周围找类似的路,这样就可以稍微精确一点。
- 对于困难的光线路径非常有效。

- 缺点:难以估计收敛速度(放那渲染一天,可能也不好看);不能保证每个像素的相同收敛速度;所以,通常会产生“脏”的结果;因此,通常不用于渲染动画。

- 偏置光传输法
- 其一:光子映射

PS:图中焦散不严谨,caustics
- caustics:光在传播过程中被反射到同一点上,产生聚焦的现象。
- 阶段1 -光子追踪从光源发射光子,弹回来,然后在扩散表面记录光子。
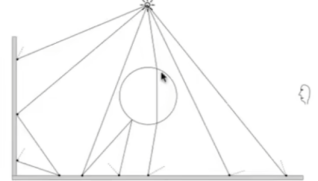
- 阶段2 -光子收集(最后的收集)从相机拍摄子路径,弹跳它们,直到它们击中漫反射表面
- 计算-局部密度估计;有更多光子的区域应该更亮;对于每个阴影点,找出最近的N个光
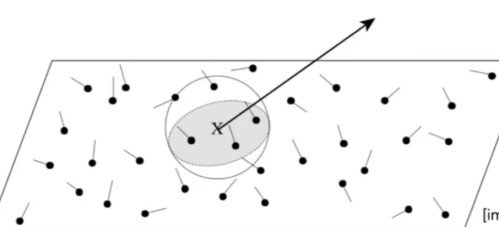
- 其二:顶点连接和合并(VCM)
- BDPT和Photon Mapping的组合
- 关键理念:让我们不要浪费BDPT中的子路径,如果它们的端点不能连接,但可以合并
- 使用光子映射来处理附近“光子”的合并
- 在很多很多领域都是用这个做的。
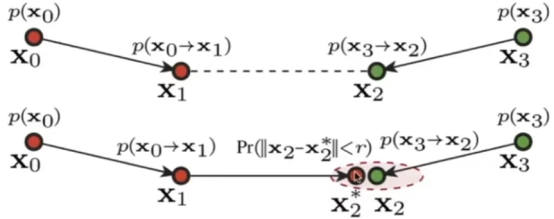
- 实时辐射度算法IR(VPL/多光法)
- 有时也被称为多光法
- 关键理念:被照亮的表面可以被视为光源
- 方法:图左在照亮场景后,我们就把它当做图二(每个被照亮的点都有一个光源),然后如图三,当我们从视角出发,去取某一个点的值时,用其他的每个光源,去照该点,最后所有光加起来的值就是最后的值。

- 优点:快速,通常可以在漫反射场景中得到很好的结果。
- 缺点:当VPLs接近阴影点时,尖峰将出现无法处理有光泽的材料
-
非表面模型:当光穿过参与的介质时,在任何一点上,它都可能被(部分)吸收和散射。
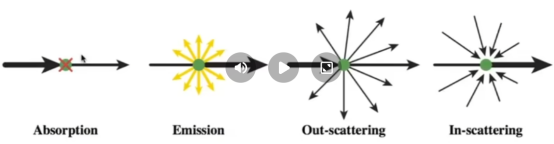
- 用相位函数描述参与介质中任意点x的光散射角分布。
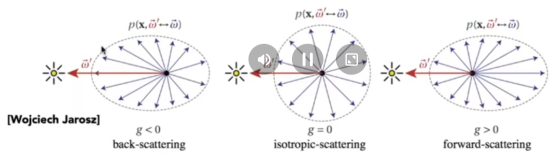
- 后来说了头发的反光等等等等,但是就单纯了解一下就行。
- 相机
成像=合成+捕获
。。。光圈、快门、ISO
- 透镜
讲了各种折射,和折射焦距成像之间的各种算法。。
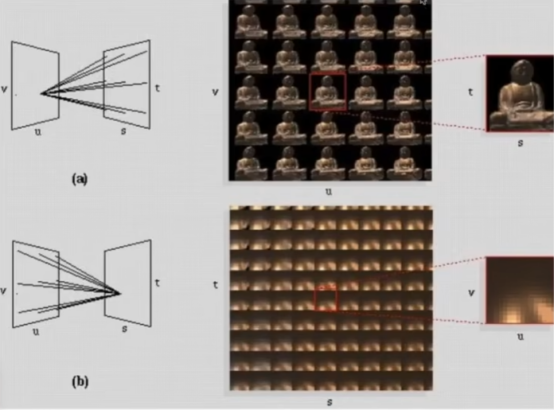
- 光场

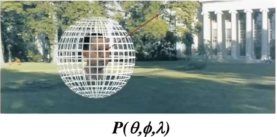
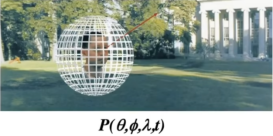

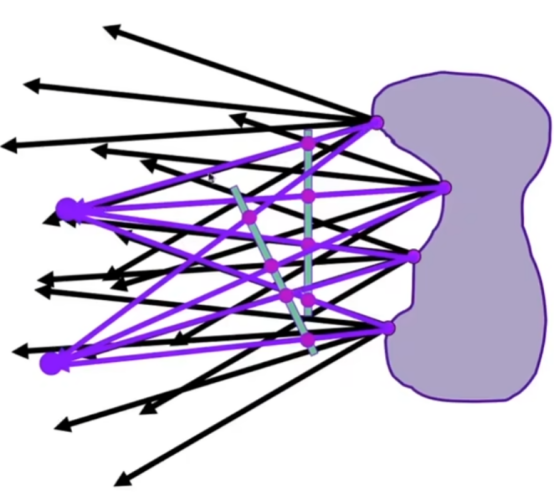
- 一个物体,会向外面不同角度射出不同的光线,这个就是物体的光场。
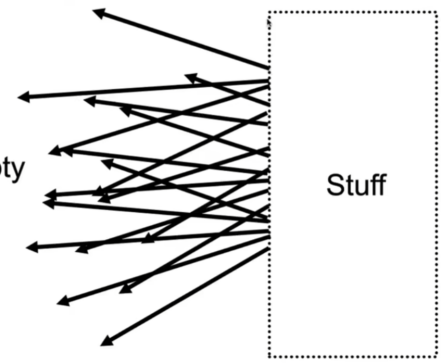
- 但我们在应用的时候,不使用物体,而是去把物体某个点往某个方向发射的光线用平面记录下来。,如上图是把光线记录在stuff的左平面,不过一个平面是不够的。
-
正确操作是下图。两个平面记录uv每个点的光线往st每个方向的信息。
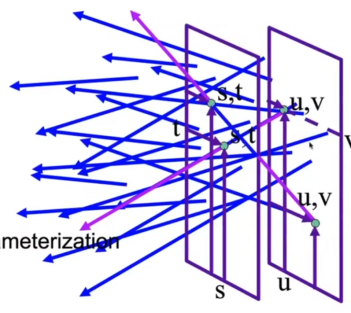
- 下图理解了就理解了。
- 色彩
- rgb、hsl、xyz、cmyk等等的各种成像原理
- 色彩其实是人眼感知出来的东西
- 法国Cie公司发明了很多种很好用的颜色空间发布在计算机上。

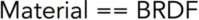

 浙公网安备 33010602011771号
浙公网安备 33010602011771号