树

1.树的基本概念：

1）根节点：指树中最上层的那个节点，整个树中有且仅有1个；

2）父节点：指与某个节点直接相连的上层节点，除根节点以外的每个节点最多有1个父节点；

3）兄弟节点：指父节点相同的同级节点；

4）子节点：该节点衍生出来的与该节点直接相连的节点称为子节点；

5）叶子节点：没有子节点的节点；

6）子树：节点的某个分支整体称为一个子树；

7）高度/深度：树的最大层数。

 

 

2.二叉树

概念：每个节点最多只有2个子节点（分别为左子节点、右子节点）的树称为二叉树。

2.1 两种特殊结构的二叉树

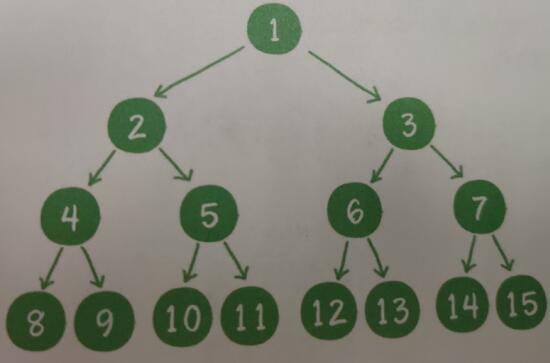
2.1.1满二叉树

当一个二叉树满足：1）任意非叶子节点都有左右子节点且2）所有叶子节点均在同一层。这个二叉树称为满二叉树。

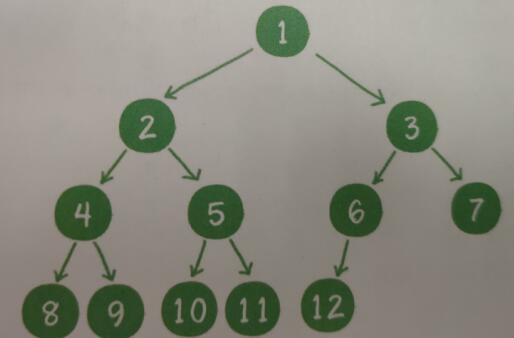
2.1.2完全二叉树

当包含n个节点的二叉树满足：若设定节点编号规则为1,2，。。。。层从左至右节点编号依次是1,2，....，n。满二叉树的1-n任意编号节点在该二叉树均存在。则该二叉树称为完全二叉树。

 

2.2 二叉树的存储结构

二叉树是一种逻辑结构，有2种物理存储方式：链表结构方式和数组结构方式。

2.2.1 链表结构

链表结构的二叉树的每个节点有3个成员：元素值、指向左子节点的指针、指向右子节点的指针。

2.2.2数组结构

在数组结构的二叉树中，根节点存储在[0]，根节点的左子结点存储在[1]，根节点的右子节点存储在[2]。总结起来，下标为parent的节点的左子节点的下标为(parent*2)+1，右子节点的下标为(parent*2)+2。如果节点的某个子节点不存在，那么存放它的数组元素为Null。

 

2.3 二叉查找树

若规定：任意节点的左子结点都要小于该节点，而右子节点大于该节点，就可以得到二叉查找树。节点分布均匀的二叉查找树的任意查找的时间复杂度为O(logn)。

 

 

3.二叉树的遍历

3.1 深度优先遍历

深度优先遍历分为前序遍历（根、左、右）、中序遍历（左、根、右）、后序遍历（左、右、根）。

深度优先遍历有递归方式和非递归方式。非递归方式需要借助一个栈来实现。

 

3.2广度优先遍历

广度优先遍历即层级遍历。从第一层开始，从最左的节点遍历到最右的节点，直到最深的一层。

层级遍历需要借助队列来实现。