Image as Set of Points, ICLR2023 论文解读

Image as Set of Points

目录

• Image as Set of Points
  • 3. METHOD
    • 3.1 Context Clusters Pipline
    • 3.2 Context Cluster Operation
    • 关键代码介绍
    • class PointReducer
    • null

• Paper 链接
• GitHub 链接

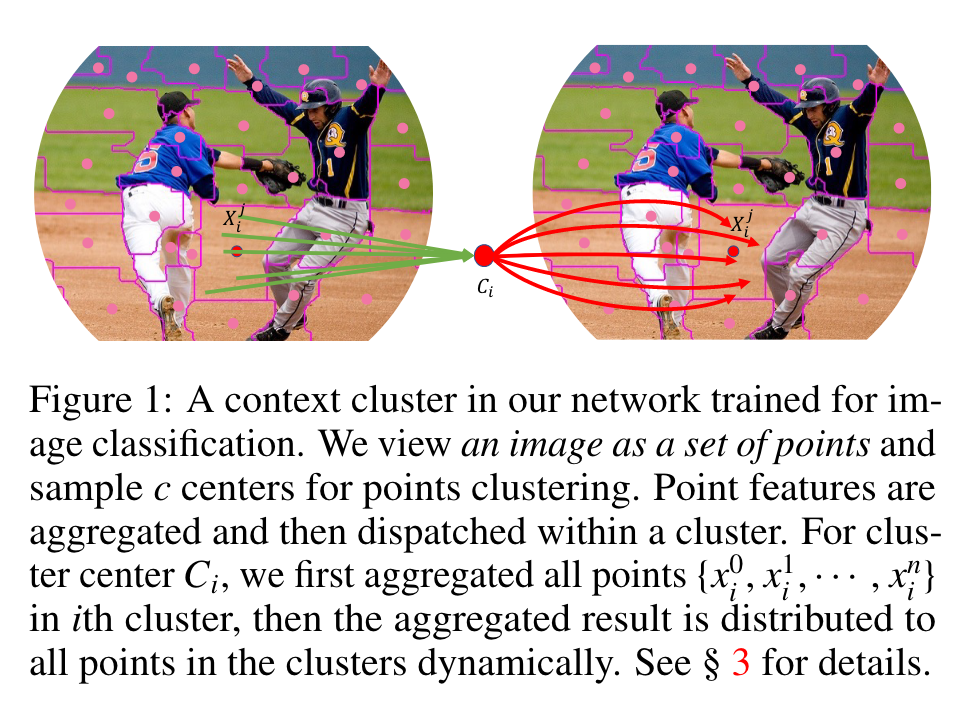
3. METHOD

Context Clusters 放弃了流行的卷积或注意力，转而采用新颖的经典算法聚类来表示视觉学习。在本节中，我们首先描述上下文集群管道。然后彻底解释了所提出的用于特征提取的上下文聚类操作（如图 2 所示）。之后，我们设置了 Context Cluster 架构。最后，一些公开的讨论可能会帮助个人理解我们的工作并在我们的 Context Cluster 之后探索更多方向。

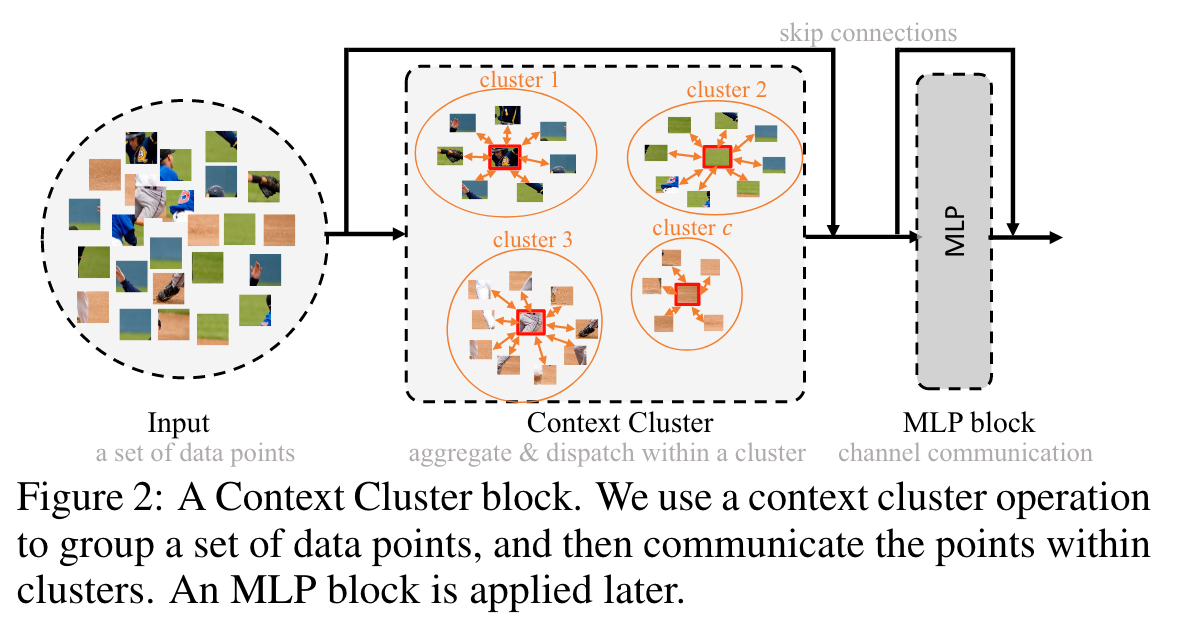
3.1 Context Clusters Pipline

From Image to Set of Points

给定输入图像 \(\mathbf{I} \in \mathbb{R}^{3\times w\times h}\)，我们首先使用每个像素 \(\mathbf{I}_{i, j}\) 的二维坐标增强图像，其中每个像素的坐标表示为 \(\left[\frac{i}{w} - 0.5, \frac{j}{h}-0.5\right]\)。研究进一步的位置增强技术以潜在地提高性能是可行的。前面这种设计考虑到它的简单性和实用性。然后将增强图像转换为点（即像素）的集合 \(\mathbf{P} \in \mathbb{R}^{5\times n}\)，其中 \(n = w \times h\) 是点的数量，每个点都包含特征（颜色）和位置（坐标）信息；因此，点集可能是无序和无组织的。（为啥要做这个？）

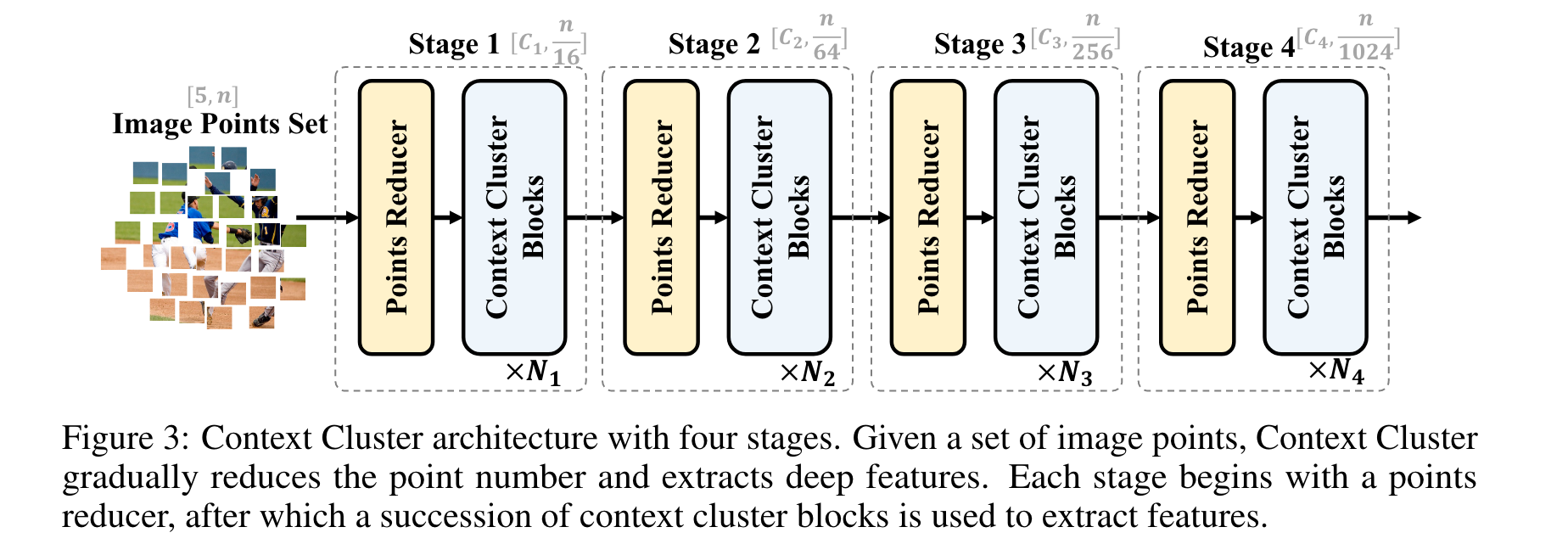
图 3：具有四个阶段的 Context Cluster 架构。给定一组图像点，Context Cluster 逐渐减少点数并提取深层特征。每个阶段都先过一个点缩减器，然后使用一系列 CoCs 来提取特征。

通过提供一个理解图像的全新视角，也就是图像点，我们获得了惊人的泛化能力。一组数据点可以被视为通用数据表示，因为大多数领域的数据可以作为特征和位置信息的组合（或两者之一）来给出。这启发我们将图像概念化为一组点。（和点云形式类似？）

Feature Extraction with Image Set Points （讲特征提取的架构）

按照 ConvNets 方法，我们使用 CoCs 块（参见图 2 以供参考，参见第 3.2 节以进行解释）分层提取深层特征。图 3 显示了我们的 CoCs 架构。给定一组点 \(\mathbf{P} \in \mathbb{R}^{5\times n}\)，我们首先减少点数以提高计算效率，然后应用一系列 CoCs 块来提取特征。为了减少点数，我们在空间中均匀地选择（什么是均匀选择，更具体的，或者代码的表述？实际上，就是平分，可以参考后面的 class PointReducer）一些锚点，最近的 k 个点通过线性投影连接和融合。请注意，如果所有点都按顺序排列并且 k 设置正确（即 4 和 9），则可以通过卷积运算来实现这种降采样，就像在 ViT 中一样（Dosovitskiy 等人，2020）。为了清楚前面所述的中心和锚点（如何选择），我们强烈建议读者查看附录B。

附录B 解读：关于 CoCs 中心和锚点的解释

人们可能会对如何在我们的 point reducer 块中指定锚点和在我们的 CoCs 块中指定聚类中心感到困惑。我们在本节中提供了对它们的说明性和详尽的解释。

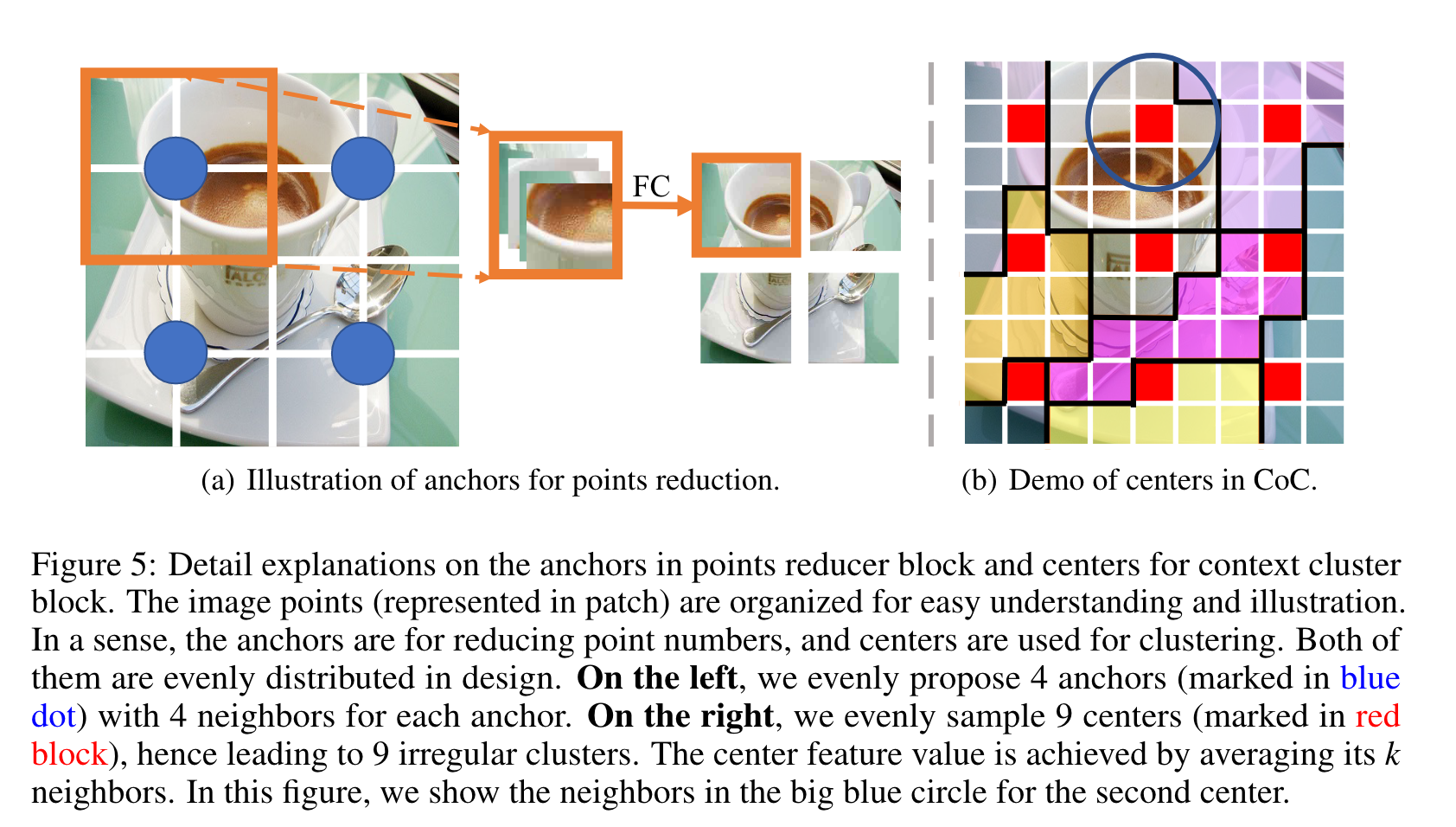
对于锚点和中心，它们在空间中均匀生成。为了更好地说明这一点，我们在下图中绘制了组织好的图像点。

图像点（以小块表示）被组织（规整）起来以便于理解和说明。锚（anchors）是为了减少点数，而中心（centers）是用来聚类的。两者被设计为均匀分布。在左侧，我们均匀地提出 4 个锚点（用蓝点标记），每个锚点有 4 个邻居（可能是使用网格的坐标来计算距离）。在右侧，我们均匀地采样 9 个中心（以红色块标记），因此导致 9 个不规则簇。（具体是如何聚类的，如何度量距离，看后面 3.2）中心特征值是通过平均它的 k 个邻居来获得的。在此图中，我们在第二个中心的蓝色大圆圈中显示了邻居。

如左图，我们展示了16个图像块（点），和4个被设置的锚点，用于进行下采样，每个锚点都考虑它最近的 \(4\) 个邻居。然后，他们全部按 通道 维串联起来，然后通过 \(FC\) 来降低维数并融合信息。在减少点的数量后，我们得到一个新的点集，该点集的数量和设置的锚点的数量相同。

右图中，我们展示了9个中心块，也就是红色的块以及对应的9个簇。其中，生成中心的特征由 \(k\) 个邻居的平均给出，例如图中第二个红色点的特征由蓝色圆圈中9个点来进行平均。

聚类时的邻居的数量可以是任何数值。我们将其设定为 \(4\) 或 \(9\) （整数的幂），原因有三：

• 首先，我们遵循 ConvNets 和 pyramid ViTs 的设计，以确保点的集合可以被重组为一个矩形的特征图。
• 其次，这种策略通过采用卷积或池化操作（前文说了）可以简化我们的代码（就是方便写 KNN）。
• 最后，大多数检测和分割方法都需要一个矩形的特征图。（这里其实不理解，但是实际上可能是恰当的 \(k\) 方便后面做上采样）。

附录看完后，还是有一点问题，没有理解它是如何聚类的，用什么进行度量。｜在后文 3.2 中提到

Task-Specific Applications.

对于分类，我们对最后一个块输出的所有点进行一个池化（平均），并使用 FC 层进行分类。

对于检测和分割等下游密集预测任务，我们需要在每个阶段后按位置重新排列输出点，以满足大多数检测和分割头的需求（例如 Mask-RCNN）。换句话说，Context Cluster 在分类任务中提供了显著的灵活性，但限于密集预测任务的要求和我们的模型配置之间的妥协。我们希望创新的检测和分割头（如DETR（Carion等人，2020））能与我们的方法无缝整合。

3.2 Context Cluster Operation

在本小节中，我们将介绍我们工作中的关键贡献，Context Cluster 操作。整体上，我们首先将特征点分组为簇；然后，每个簇中的特征点将被聚合，然后 dispatched 回来，如图 1 所示。

Context Clustering 给定一组特征点 \(\mathrm{P} \in R^{n\times d}\)，我们根据相似性将所有点分为几组，每个点单独分配给一个簇。我们首先将 P 线性投影（理解成 \(FC\) 可以）到 \(P_s\) 以进行相似度计算。遵循传统的 SuperPixel 方法 SLIC ，我们在空间中均匀地提出 \(c\) 个中心，中心特征是通过对其 \(k\) 个最近点求平均来计算的。然后我们计算 \(P_s\) 和中心点集之间的余弦相似度矩阵 \(\mathbf{S} \in R^{c\times n}\)。由于每个点都包含特征和位置信息，在计算相似度时，我们隐式地突出了点的距离（局部性）以及特征相似度（没搞懂）。之后，我们将每个点分配到最相似的中心，从而产生 \(c\) 个簇。值得注意的是，每个集群可能有不同数量的点。在极端情况下，一些集群可能有零点，在这种情况下它们是冗余的。

Feature Aggregating 我们根据与中心点的相似性，动态地聚合一个聚类中的所有点。假设一个簇包含 \(m\) 个点（\(\mathbf{P}|\mathbf{P}\in \mathbb{R}^{5\times n}\) 中的一个子集），\(m\) 个点和中心点的相似度为 \(s \in \mathbb{R}^m\)（ \(\mathbf{S}\) 中的一个子集），我们将这些点映射到一个值空间（怎么映射的？如何确定 \(d^\prime\)），得到 \(\mathbf{P}_v\in \mathbb{R}^{m×d^\prime}\)，其中 \(d^\prime\)是值空间的维度。我们也像聚类中心的一样在值空间中提出一个中心 \(v_c\)。聚合的特征 \(g\in \mathbb{R}^{d^\prime}\)由以下方式给出:

\[g=\frac{1}{\mathcal{C}}\left(v_c+\sum_{i=1}^m \operatorname{sig}\left(\alpha s_i+\beta\right) * v_i\right), \quad \text { s.t., } \mathcal{C}=1+\sum_{i=1}^m \operatorname{sig}\left(\alpha s_i+\beta\right) . \]

• 这里 \(\alpha\) 和 \(\beta\) 是可学习的标量, 用于缩放和移动。

• \(\operatorname{sig}(\cdot)\) 是 Sigmoid 函数, 用于重新缩放相似度到 \((0,1)\) 。 为什么不用 Softmax 呢？ ^[1]

• \(v_i\) 表示 \(P_v\) 中的第 \(i\) 个点。

从经验上看, 这种策略比直接应用原始相似度的结果要好得多, 因为不涉及负值。我们将价值中心 \(v_c\) 纳入公式\((1)\)用于数值稳定性^[2] 以及进一步强调局部性。为了控制幅度，引入特征因子 \(C\) 进行归一化。

Feature Dispatching 然后，聚合的特征 \(g\) 根据相似性自适应地分配到聚类中的每个点。通过这样做，点之间可以相互通信，并共享来自 Cluster 中所有点的特征（如图1所示）方法如下：

\[p_i^\prime = p_i + \mathrm{FC}(\mathrm{sig}(\alpha s_i + \beta ) * g). \]

这里，作者遵循和\((1)\)式相似的做法来处理相似性，并应用一个全连接 (FC) 层来匹配特征维度 (从值空间维度 \(d^\prime\) 到原始维度 \(d\) )。

Multi-Head Computing 考虑到 ViT 中使用的多头注意力机制，作者在上下文聚类模块中使用了类似的做法，也使用了 ℎ 个 head，且多头操作的输出由 FC 层融合，发现多头机制也使得模型效果更好。 Multi-headed Self-attention（多头自注意力）机制介绍

关键代码介绍

class PointReducer

官方 GitHub 居然有一个 typo （Reducer打错了），感觉可以提 PR。

class PointReducer(nn.Module):
    """
    Point Reducer is implemented by a layer of conv since it is mathmatically equal.
    Input: tensor in shape [B, C, H, W]
    Output: tensor in shape [B, C, H/stride, W/stride]
    """

    def __init__(self, patch_size=16, stride=16, padding=0,
                 in_chans=3, embed_dim=768, norm_layer=None):
        super().__init__()
        # to_2tuple(x): (x, x)
        patch_size = to_2tuple(patch_size)
        stride = to_2tuple(stride)
        padding = to_2tuple(padding)
        # proj: 投影，把分 patch 和 FC 操作合并了，所有 kernel_size = stride
        self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size,
                              stride=stride, padding=padding)
        self.norm = norm_layer(embed_dim) if norm_layer else nn.Identity()

    def forward(self, x):
        x = self.proj(x)
        x = self.norm(x)
        return 

这段代码本质上是用于图像处理的自注意力机制的实现，这里用作 PointReduce，其中self.proj是一个卷积层对象，用于将图像的每个局部区域（patch）映射到一个低维的特征空间中。

具体来说，这个卷积层的输入通道数为in_chans，表示输入图像的通道数，输出通道数为embed_dim，表示每个局部区域映射到特征空间中的维度数。卷积核的大小为kernel_size，表示每个局部区域的大小，stride和padding分别表示卷积的步长和填充。

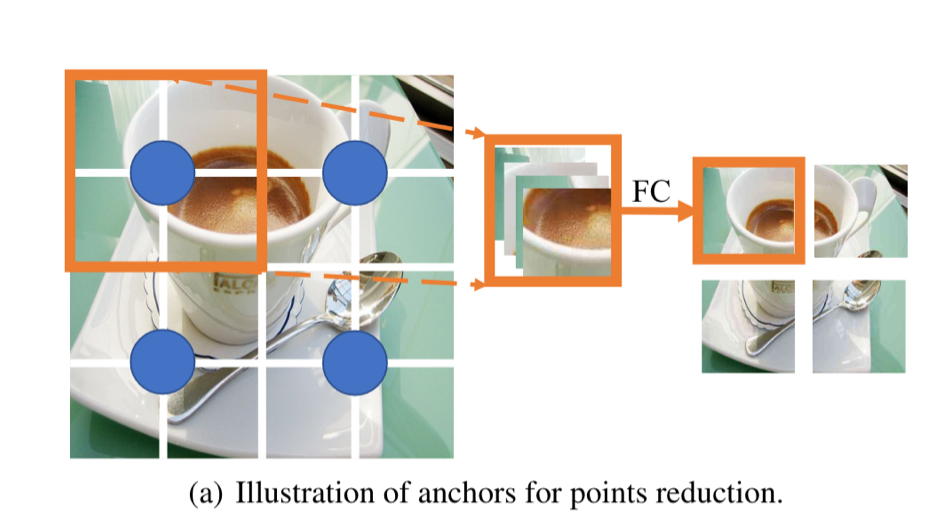
但是这里，我们实际上做的是上图的工作，所以我们把 \(\mathtt{kernel\_size }\) 设置为和 \(\mathtt{stride}\) 相同就可以直接一步实现了。

---

1. Softmax is not considered since the points do not contradict with one another. ↩︎

2. If there were no \(v_c\) involved and no points are grouped into the cluster coincidentally, \(C\) would be zero, and the network cannot be optimized. In our research, this conundrum occurs frequently. Adding a small value like \(1e^{−5}\) does not help and would lead to the problem of vanishing gradients. ↩︎