C++之快速幂例题

P3390 【模板】矩阵快速幂

题目传送门

题目背景

矩阵快速幂

题目描述

给定 n×n 的矩阵 A，求 Ak。

输入格式

第一行两个整数 n,k 接下来 n 行，每行 n 个整数，第 i 行的第 j 的数表示 Ai,j​。

输出格式

输出 A^k

共 n 行，每行 n 个数，第 i 行第 j 个数表示 (Ak)i,j​，每个元素对 10^9+7 取模。

输入输出样例

输入 #1复制

2 1
1 1
1 1

输出 #1复制

1 1
1 1

嗯，好吧，步入正题，这是一道洛谷的模板题，本以为能爆踩他的我，结果可想而知。

后来，我总结了一下错误原因，结果发现，我原来主函数里少写一行代码（就无语），然后我就又又又瞎想了一些奇奇怪怪的东西：

快速幂其实就是用的递归公式：

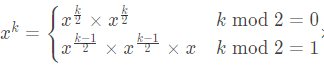
所以，我们用这个推出的代码就应该长这样：

while版：

while(x>0) {
    if(x%2!=0) ans=ans*a;
        a=a*a;
        x=x>>1;
}

递归版：

int K(int a,int n){
    if(n==0)    
            return 1;
    if(n==1)    
            return a;
    int c=K(a,n/2);
    if(n%2==0)    
            return c*c;
    else    
            return c*c*a;
}    

这说明什么？？？我们可以用这几段代码稍加修改，把它变成这道题的代码

BUT：！！！它超时了（TLE）

while也不行

呵呵，所以经过我的精心修改，正确的代码他终于来了！！

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#define LL long long//我真懒，呵呵 
#define MOD 1000000007
using namespace std;
LL a[109][109],ans[109][109],cil[109][109],K;//个人习惯 
int n;
void Fk() {
    while(K) {
        if(K%2) {
            for(int i=1; i<=n; i++)
                for(int j=1; j<=n; j++)
                    cil[i][j]=ans[i][j],ans[i][j]=0;
            for(int i=1; i<=n; i++)
                for(int j=1; j<=n; j++)
                    for(int k=1; k<=n; k++)
                        ans[i][j]=(ans[i][j]+cil[i][k]*a[k][j]%MOD)%MOD;
        }
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                cil[i][j]=a[i][j],a[i][j]=0;
        for(int i=1; i<=n; i++)
            for(int j=1; j<=n; j++)
                for(int k=1; k<=n; k++)
                    a[i][j]=(a[i][j]+cil[i][k]*cil[k][j]%MOD)%MOD;

        K/=2;
    }
}
int main() {
    scanf("%d%lld",&n,&K);
    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            scanf("%lld",&a[i][j]);

    for(int i=1; i<=n; i++)
        for(int j=1; j<=n; j++)
            ans[i][j]=a[i][j];


    K--;
    Fk();

    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++) printf("%lld ",ans[i][j]);
        puts("");
    }
    return 0;
}

我滴CSDN博客