C++树状结构之二叉树

二叉树形式与性质
首先，二叉树有这么几种性质，他的性质在编辑程序的时候是至关重要的，绝不可以忘记那么，我们来看一下这几种性质吧：

  

二叉树还有五种形式，

 

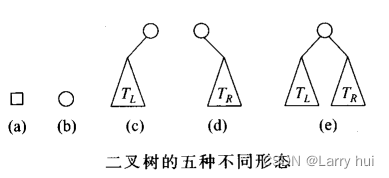
这五种形式分别是：

满二叉树：每层都是满的；

完全二叉树：除最后一层外，每层都是满的，并且或者最后一层是满的，或者是在右边缺少连续若

干结点;

空树：没有节点

根树：一个节点

斜树：左斜树，右斜树

怎么求二叉树有多少节点呢？我们看一下代码：

int TreeSize(BTNode* root) {
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

二叉树的深度与度：
深度
深度为n，最多有2ⁿ-1个结点【n≥1】第i层，最多有2的（i-1）次方个结点；具有n个结点的完全二

叉树的深度为 floor(log2n)+1

度
1、结点所拥有的子树的个数

2、树中各结点度的最大值称为该树的度，叶子结点就是度为0的结点

例 n0：度为0的结点数，n1:度为1的结点 n2：度为2的结点数

对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；

入度与出度：

入度即指共有多少边连接此节点，出度指从此节点出去共有几条边。

例题1：
一棵树度为4，其中度为1，2，3，4的结点个数分别为4，2，1，1，则这棵树的叶子节点个数为多少？

解：因为任一棵树中，结点总数=度数*该度数对应的结点数+1，所以：

n0+4+2+1+1 = （0*n0 + 1*4 + 2*2 + 3*1 + 4*1）+1

则：n0=8

其中：n0表示叶子结点。

例题2：
一颗二叉树的叶子节点有5个，度为1的结点有3个，该二叉树的结点总个数是？

N0 = N2+1

N0 = 5 则 N2 = 4

N = N0+N1+n2

=5+3+4

=12

例题3：
深度为7的完全二叉树共有125个结点，则该完全二叉树的叶子结点为？

h = 7 ->125

h = 6 ->满二叉树*2^6 - 1=63

则最后一层有125 - 63 = 62个

此外第六层有1个叶节点

62 + 1 = 63个

遍历：
二叉树还有三种特有的遍历方式，它们分别是：前序遍历、中序遍历、后序遍历。

这三种方式，其实他的意思就是前根序遍历，中根序遍历和后根序遍历。

三种方式的遍历方式分别是：根-左-右，左-根-右，左-右-根。

左子树比右子树的要靠前，举个例子：

 

 

 

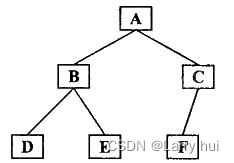
前序遍历:先访问根，再左子树，接右子树。

顺序为：A,B,D,E,C,F

中序遍历:先访问左子树，再根，接右子树。

顺序为：D,B,E,A,F,C

后序遍历:先访问左子树，再右子树，接根。

顺序为：D,E,B,F,C,A

(二叉树为空直接返回)

知道了两种遍历的结果，就能把第三种推出来，来一道题试看一下

例题1：P1305 新二叉树

题目描述

输入一串二叉树，输出其前序遍历。

输入格式

第一行为二叉树的节点数 nn。(1≤n≤26)

后面 nn 行，每一个字母为节点，后两个字母分别为其左右儿子。特别地，数据保证第一行读入的节点必为根节点。

空节点用 * 表示

输出格式

二叉树的前序遍历。

输入输出样例

输入 #1复制

6
abc
bdi
cj*
d**
i**
j**
输出 #1复制

abdicj
解：

#include<bits/stdc++.h>
using namespace std;
int n, l[50], r[50], root;
string str;
void preorder(int t) {
    if (t == ('*' - 'a')) {
        return;
    }
    cout << char('a' + t);
    preorder(l[t]);
    preorder(r[t]);
}
int main() {
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> str;
        if (!i) {
            root = str[0] - 'a';
        }
        l[str[0] - 'a'] = str[1] - 'a';
        r[str[0] - 'a'] = str[2] - 'a';
    }
    preorder(root);
    return 0;
}

二叉树结点名称与关系
二叉树的某个节点与一指定节点的关系是有名称的，我们附图讲解一下：

 

 

 

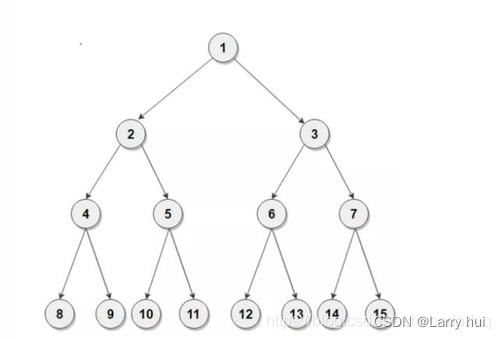
八号节点是一个叶节点，他的父节点是四号，父节点的意思就是从这个节点往上的一个节点，这

个节点是一个枝节点。

祖先节点是指某一个节点往上直至根节点的所有点（包括此节点，就是自己也是自己的祖先），举

个例子：13号节点的祖先节点是包括13号在内的13，6，3，1

12号节点与13号节点的公共祖先有6，3，1；最近公共祖先是6.

当然，还有子节点，子节点是指某节点所分支下来的一个节点，就是比这个节点所在的层下一层的

直接分支，举个例子，4号节点的子节点是8号与9号。

孙子节点：就是指某个节点的非直接分支（就是间接分支），通俗一点就是分支的分支。

例题：

P3379 【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 N,M,SN,M,S，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 N-1N−1 行每行包含两个正整数 x, yx,y，表示 xx 结点和 yy 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 MM 行每行包含两个正整数 a, ba,b，表示询问 aa 结点和 bb 结点的最近公共祖先。

输出格式

输出包含 MM 行，每行包含一个正整数，依次为每一个询问的结果。

输入输出样例

输入 #1复制

5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
输出 #1复制

4
4
1
4
4
说明/提示

对于 30\%30% 的数据，M< 10M≤10。

对于 70\%70% 的数据M\leq 10000M≤10000。

对于 100\%100% 的数据M\leq 500000M≤500000。

样例说明：

该树结构如下：

 

第一次询问：2, 42,4 的最近公共祖先，故为 44。

第二次询问：3, 23,2 的最近公共祖先，故为 44。

第三次询问：3, 53,5 的最近公共祖先，故为 11。

第四次询问：1, 21,2 的最近公共祖先，故为 44。

第五次询问：4, 54,5 的最近公共祖先，故为 44。

故输出依次为 4, 4, 1, 4, 44,4,1,4,4。

2021/10/4 数据更新 @fstqwq：应要求加了两组数据卡掉了暴力跳。

解：

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#define int long long
using namespace std;
const int maxn=5e5+5;
typedef struct Edge {
    int next,to;
} edg;
edg e[maxn<<1];
int n,m,s,cnt,head[maxn<<1];
void AddEdge(int u,int v) {
    e[cnt].to=v;
    e[cnt].next=head[u];
    head[u]=cnt++;
}
int fa[maxn],son[maxn],depth[maxn],siz[maxn];
void dfs1(int u,int f) {
    fa[u]=f;
    depth[u]=depth[f]+1;
    siz[u]=1;
    int maxsize=-1;
    for(int i=head[u]; ~i; i=e[i].next) {
        int v=e[i].to;
        if(v==f)
            continue;
        dfs1(v,u);
        siz[u]+=siz[v];
        if(siz[v]>maxsize) {
            maxsize=siz[v];
            son[u]=v;
        }
    }
}
int tim,dfn[maxn],top[maxn];
void dfs2(int u,int t) {
    dfn[u]=++tim;
    top[u]=t;
    if(!son[u])
        return;
    dfs2(son[u],t);
    for(int i=head[u]; ~i; i=e[i].next) {
        int v=e[i].to;
        if(v==fa[u]||v==son[u])
            continue;
        dfs2(v,v);
    }
}
int query(int x,int y) {
    while(top[x]!=top[y]) {
        if(depth[top[x]]<depth[top[y]])
            swap(x,y);
        x=fa[top[x]];
    }
    if(depth[x]>depth[y])
        swap(x,y);
    return x;
}
signed main() {
    memset(head,-1,sizeof(head));
    scanf("%lld%lld%lld",&n,&m,&s);
    int N=n-1;
    while(N--) {
        int u,v;
        scanf("%lld%lld",&u,&v);
        AddEdge(u,v);
        AddEdge(v,u);
    }
    dfs1(s,s);
    dfs2(s,s);
    while(m--) {
        int x,y;
        scanf("%lld%lld",&x,&y);
        int ans=query(x,y);
        cout<<ans<<endl;
    }
}

我的CSDN博客