折半搜索入门-CF888E Maximum Subsequence

https://codeforces.com/problemset/problem/888/E
一道入门折半搜索题.
题意是:在a数组中选择若干数使得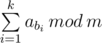最大(1 ≤ n ≤ 35)
直接爆搜的复杂度2³⁵肯定是不能接受的,折半搜索2^(18.5)的复杂度是可通过的.
先对前n/2的区域进行搜索,然后把搜索结果存储在vector b中
在后n/2的区域中在搜索到末尾n的时候使用lower_bound去寻找小于m - b[i]的值(等于的话会变成0),同时考虑一点即lower_bound可能会遍历到b数组末尾,则对b[size() - 1]这个点进行特判操作
剩下的就很常规了.

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int inf = 3e18;
int T;
int n,k;
int a[38];
int ans = -inf;
vector<int>b;
void dfs1(int dep,int sum){
    if(dep == n / 2 + 1){
        b.push_back(sum);
        return;
    }
    dfs1(dep + 1,(sum + a[dep])%k);
    dfs1(dep + 1,sum);
}
void dfs2(int dep,int sum){
    if(dep == n + 1){
    int pos = (lower_bound(b.begin(),b.end(),k - sum) - 1 - b.begin());
        ans = max(ans,b[pos] + sum);
        ans = max(ans,(b[b.size() - 1] + sum) % k);    
        return;
    }
    dfs2(dep + 1,sum);
    dfs2(dep + 1,(sum + a[dep])%k);
}
void solve(){
    cin>>n>>k;
    for(int i = 1;i<=n;++i){
        cin>>a[i];
    }
    dfs1(1,0);
    sort(b.begin(),b.end());
    dfs2(n/2 + 1,0);
    cout<<ans;
}
signed main() {
    cin.tie(nullptr)->sync_with_stdio(0);
    T = 1;
   while(T--){
       solve();
   }
    return 0;
}