heaviside step function
heaviside step function:阶跃函数
The function is used in the mathematics of control theory and signal processing to represent a signal that switches on at a specified time and stays switched on indefinitely. It was named after the English polymath Oliver Heaviside.
It is the cumulative distribution function of a random variable which is almost surely 0. (See constant random variable.)
The Heaviside function is the integral of the Dirac delta function: H′ = δ. This is sometimes written as
although this expansion may not hold (or even make sense) for x = 0, depending on which formalism one uses to give meaning to integrals involving δ.
example:
![H[n]=\begin{cases} 0, & n < 0 \\ 1, & n \ge 0 \end{cases}](http://upload.wikimedia.org/math/7/4/1/7410747ec7563eab51f608f2c80a9497.png)


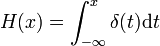

 浙公网安备 33010602011771号
浙公网安备 33010602011771号