[USACO21JAN] Sum of Distances P 题解
这个题也太妙了,考场根本一点头绪没有。
给定一些图,求这些图的张量积中 \((1,1,\cdots,1)\) 到所有点的最短路和。
首先我们发现这个张量积上的最短路有什么特点,我们可以考虑将所有图分开考虑,每一张图分开做,加入从 \((1,1,\cdots,1)\) 到 \((a_1,a_2,\cdots,a_K)\),可以看成分别从 \(1\) 到 \(a_1\),\(1\) 到 \(a_2\),\(\cdots\),\(1\) 到 \(a_K\),同时到达。
我们发现图是无向图,所以可以通过在一条边反复走来达到等待的目的,所以就只和最短路长度的奇偶性相关。
考虑算出每张图上每个点的奇偶最短路,设第 \(i\) 张图中 \(1\) 到 \(j\) 的长度为奇数的最短路长度为 \(\text{odd}_{i,j}\),长度为偶数为 \(\text{even}_{i,j}\),那么 \((1,1,\cdots,1)\) 到 \((a_1,a_2,\cdots,a_K)\) 的最短路长度为 \(\min\{\max_{i=1}^K\{\text{odd}_{i,a_i}\},\max_{i=1}^K\{\text{even}_{i,a_i}\}\}\),这个东西是 \(\min\) 套 \(\max\),并不是很好处理,所以考虑进行一步转化,将 \( \min\) 展开成 \(\max\),最后我们就是要求这样一个式子:
发现可以把三个式子分开来算,这样形式是一样的,最后就是要算这样一个东西:
考虑这个 \(V\) 的范围只有 \(n\),所以可以统计 \(\max_{i=1}^K\{V_{i,a_i}\}=x\) 的 \((a_1,a_2,\cdots,a_n)\) 的数量。
然后再考虑这个新的式子怎么算,其实也不难,因为求得是 \(\max\),又是计数,可以考虑两两合并,这样就只要考虑相邻两项,算以下式子:
其中 \(A_x\),\(B_x\) 分别代表待合并的两个数组中满足 \(\max_{i=1}^K\{V_{i,a_i}\}=x\) 的数量,\(F_x\) 同理,不过是合并结果。
这个式子很像卷积,但显然不是正常的多项式卷积或是位运算卷积之类的,所以肯定不是什么 FFT 或者 FWT 之类的。
这个可以形象地称为 \(\max\) 卷积的东西算起来相对 FFT 或者 FWT 更简单地多,但我们可以思考做一种类似 FFT 中 DFT 和 IDFT 的变换来使其成为一种线性变换,发现这个东西可以用一种非常简单的办法,就是直接前缀和,逆变换就是直接再差分回来就好了,读者可以手模一下,具体原理可以看下面这张图:
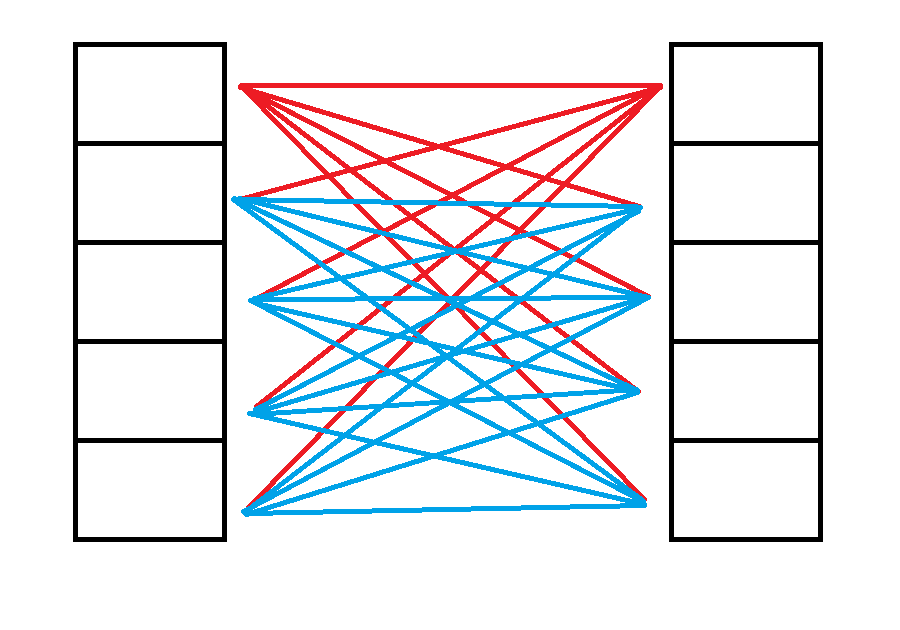
这里黑色的格子表示两个要合并的数组,红线表示待求值最顶层要算的,红线和蓝线的和正好是前缀和的积,而蓝线也是前缀和的积,做差分就能得到答案。
这样整道题就做完了,但还有一个细节。
两个数组和合并是 \(\mathcal O\left(\text{len}\right)\) 的,如果直接将所有数组合并时间复杂度会退化成 \(\mathcal O\left(Kn\right)\),会被卡掉,怎样优化呢?其实直接将数组按长度从小到大合并就好了,这样时间复杂度就是 \(\mathcal O\left(\sum n\right)\),是可过的。
c++ 代码
#include<bits/stdc++.h>
using namespace std;
#define Reimu inline void // 灵梦赛高
#define Marisa inline int // 魔理沙赛高
#define Sanae inline bool // 早苗赛高
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> Pii;
typedef tuple<int, int, int> Tiii;
#define fi first
#define se second
const int P = 1e9 + 7;
Marisa add(int x, int y) { return (x += y) < P ? x : x - P; }
Marisa&Add(int&x, int y) { return (x += y) < P ? x : x -= P; }
Marisa sub(int x, int y) { return (x -= y) < 0 ? x + P : x; }
Marisa&Sub(int&x, int y) { return (x -= y) < 0 ? x += P : x; }
Marisa mul(int x, int y) { return 1LL * x * y % P; }
Marisa&Mul(int&x, int y) { return x = 1LL * x * y % P; }
Marisa qpow(int x, int y) { int res = 1; for (; y; y >>= 1, Mul(x, x)) if (y & 1) Mul(res, x); return res; }
const int N = 100010, M = 50010;
int c, n, m;
int dis[N][2];
vector<int> G[N], d0[M], d1[M], d[M];
Sanae cmp(vector<int> &a, vector<int> &b) { return a.size() < b.size(); }
Reimu bfs(int k) {
const int B = 1 << 30;
memset(dis + 1, -1, sizeof(int) * n << 1);
int mx[] = {0, 0};
queue<int> Q; Q.emplace(1), dis[1][0] = 0;
while (!Q.empty()) {
int x = Q.front(), f = x >> 30; Q.pop();
for (auto y: G[x & ~B]) if (!~dis[y][!f]) Q.emplace(y | !f << 30), mx[!f] = max(mx[!f], dis[y][!f] = dis[x & ~B][f] + 1);
}
d0[k].resize(mx[0] + 1); d1[k].resize(mx[1] + 1); d[k].resize(max(mx[0], mx[1]) + 1);
for (int i = 1; i <= n; ++i) {
if (~dis[i][0]) ++d0[k][dis[i][0]];
if (~dis[i][1]) ++d1[k][dis[i][1]];
if (~dis[i][0] && ~dis[i][1]) ++d[k][max(dis[i][0], dis[i][1])];
}
}
Reimu merge(vector<int> &a, vector<int> &b) {
int len = max(a.size(), b.size());
a.resize(len); b.resize(len);
for (int i = 1; i < len; ++i) Add(a[i], a[i - 1]), Add(b[i], b[i - 1]);
for (int i = 0; i < len; ++i) Mul(a[i], b[i]);
for (int i = len - 1; i; --i) Sub(a[i], a[i - 1]);
}
Marisa calc(vector<int> *vec) {
sort(vec + 1, vec + c + 1, cmp);
for (int i = 2; i <= c; ++i) merge(vec[i], vec[i - 1]);
int res = 0;
for (int i = 1; i < vec[c].size(); ++i) Add(res, mul(i, vec[c][i]));
return res;
}
int main() {
ios::sync_with_stdio(false); cin.tie(nullptr); cout.tie(nullptr);
cin >> c;
for (int k_ = 1; k_ <= c; ++k_) {
cin >> n >> m;
for (int i = 1; i <= n; ++i) G[i].clear();
for (int i = 1, x, y; i <= m; ++i) cin >> x >> y, G[x].emplace_back(y), G[y].emplace_back(x);
bfs(k_);
}
cout << sub(add(calc(d0), calc(d1)), calc(d));
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号