顺序表
线性结构是数据结构中最基础、最简单的一种数据结构类型,其中最典型的就是线性表
线性表的定义
具有 相同特性 的数据元素的 有限 序列。
| 相同特性 | 所有元素属于同一数据类型 |
| 有限 | 数据元素个数是有限的 |
| 序列 | 数据元素由逻辑序号唯一确定 |
用逻辑序号来确定的特性使得线性表中可以有多个相同值的元素
线性表中所含元素的个数叫做线性表的长度,用n表示( n >= 0)。当n = 0时,表示线性表是一个空表,即表中不包含任何元素
线性表的逻辑表示
线性表的逻辑表示为:
(
a
1
,
a
2
,
.
.
.
,
a
i
,
a
i
+
1
,
.
.
.
,
a
n
)
a
i
(
1
≤
i
≤
n
)
表
示
第
i
个
元
素
(
i
为
逻
辑
位
序
)
\begin{aligned} &(a_1,a_2,...,a_i,a_{i+1},...,a_n)\\ &a_i(1\le i \le n )表示第i个元素(i为逻辑位序) \end{aligned}
(a1,a2,...,ai,ai+1,...,an)ai(1≤i≤n)表示第i个元素(i为逻辑位序)
线性表的基本运算
- 初始化线性表
构造一个空的线性表l - 建立线性表
- 销毁线性表
释放线性表l占用的内存空间 - 判线性表是否为空表
若为空返回1,不为空返回0 - 求线性表的长度
返回元素个数n - 输出线性表
当线性表l不为空时,顺序输出l的每一个元素 - 求线性表
l中指定位置的某个数据元素
用e返回l中第i个元素的值 - 定位查找
返回l中第一个与e相等的逻辑位序 - 插入一个数据元素
在l的第i个元素之前插入新的元素e,l的长度+1 - 删除数据元素
删除l的第i个元素,并用e返回其值,l的长度-1
线性表的顺序存储结构
把线性表中所有的元素按照顺序的方法进行存储。所有元素按逻辑顺序依次存储到存储器中一片连续的存储空间中
顺序表类型定义
#define MAXSIZE 100
typedef int ElemType;
typedef struct {
ElemType data[MAXSIZE];
int length;
}SqList;
顺序表运算的实现
初始化线性表
void initList(SqList** l) {
(*l) = (SqList*)malloc(sizeof(SqList));
(*l)->length = 0;
}
建立线性表
void createList(SqList* l, ElemType a[], int n) {
int i;
for (i = 0; i < n; i++) {
l->data[i] = a[i];
}
l->length = n;
}
销毁线性表
void destroyList(SqList* l) {
free(l);
}
判断是否为空表
int listEmpty(SqList* l) {
return (l->length == 0);
}
求线性表的长度
int listlength(SqList* l) {
return (l->length);
}
当线性表不为空时,顺序显示L中各元素的值
void dispList(SqList* l) {
int i;
if (listEmpty(l)) {
printf("线性表为空\n");
return;
}
for (i = 0; i < l->length; i++) {
printf("%d ", l->data[i]);
}
printf("\n");
}
求某个数据元素值
int getElem(SqList* l, int i, ElemType* e) {
if (i < 1 || i > l->length) {
return FALSE;
}
*e = l->data[i - 1];
/*
**物理位序 = 逻辑位序 + 1
*/
return TRUE;
}
getElem()的时间复杂度为O(1)。体现了顺序表的随机存取特性
按元素值查找
int locateElem(SqList* l, ElemType e) {
int i = 0;
while (i < l->length && l->data[i] != e) {
i++;
}
if (i >= l->length) {
return 0;
}
else {
return i + 1;
/*
** 返回的是逻辑位序
*/
}
}
插入数据元素
在插入之前,已有的元素要给新来的元素腾出空间,后面的元素都要向表尾移动一位。最后表的长度+1

int listInsert(SqList* l, int i, ElemType e) {
int j;
if (i < 1 || i > l->length + 1) { /*判断给出的下标是否合法*/
return FALSE;
}
i--;
for (j = l->length; j > i; j--) {
l->data[j] = l->data[j - 1];
}
l->data[i] = e;
l->length++;
return TRUE;
}
当i = n + 1时,元素移动次数为0,最好时间复杂度为O(1)
当i = 1时,元素移动n次,最坏时间复杂度为O(n)
线性表中有n+1个可以插入元素的地方,在插入元素ai时,若为等概率情况,则
p
i
=
1
n
+
1
p_i = \frac 1 {n+1}
pi=n+11
此时需要将ai到an的元素均向后移动一个位置,共移动n-i+1个元素
所以在长度为n的线性表中插入一个元素时所需移动元素的平均次数为
A
(
n
)
=
∑
i
=
1
n
+
1
1
n
+
1
×
(
n
−
i
+
1
)
=
1
n
+
1
∑
i
=
0
n
n
−
i
+
1
=
n
2
\begin{aligned} A(n) &= \displaystyle\sum^{n+1}_{i=1} \frac 1 {n+1} \times ( n - i + 1)\\ &= \frac 1 {n+1}\displaystyle\sum^n_{i=0} n-i+1\\ &= \frac n 2 \end{aligned}
A(n)=i=1∑n+1n+11×(n−i+1)=n+11i=0∑nn−i+1=2n
因为插入算法主要花的时间就在移动元素上,因此插入算法的平均时间复杂度为O(n)
删除元素
用后面的元素覆盖被删除元素,同时都向表头移动。最后表的长度-1

int listDelete(SqList* l, int i, ElemType* e)
{
int j;
if (i < 1 || i > l->length) { /*判断给出的下标是否合法*/
return FALSE;
}
i--;
*e = l->data[i];
for (j = i; j < l->length - 1; j++) {
l->data[j] = l->data[j + 1];
}
l->length--;
return TRUE;
}
对于本算法来说,元素移动的次数也与表长length和删除元素的位置i有关:
- 当
i = n时,移动次数为0,最好时间复杂度为O(1) - 当
i = 1时,移动次数为n-1,最坏时间复杂度为O(n)
在线性表l中共有n个可以删除元素的地方,在删除元素ai时,若为等概率情况,则
p
i
=
1
n
p_i = \frac1 n
pi=n1
此时需要将a(i+1)和an的元素均前移一个位置,共移动n-(i+1)+1=n-i个元素
A
(
n
)
=
∑
i
=
1
n
1
n
+
1
×
(
n
−
i
)
=
1
n
+
1
∑
i
=
0
n
n
−
i
=
n
−
1
2
\begin{aligned} A(n) &= \displaystyle\sum^{n}_{i=1} \frac 1 {n+1} \times ( n - i )\\ &= \frac 1 {n+1}\displaystyle\sum^n_{i=0} n-i\\ &= \frac {n-1} 2 \end{aligned}
A(n)=i=1∑nn+11×(n−i)=n+11i=0∑nn−i=2n−1
平均时间复杂度为O(n)
顺序表算法设计应用
例题1
已知长度为n的线性表A采用顺序存储结构。设计一个删除线性表中所有值为x的数据元素。要求:
- T(n) = O(n)
- S(n) = O(1)
方案一
删除一个就把后面的元素往前移动,T(n) = O(n2),S(n) = O(1),时间复杂度不符合要求
方案二
创建一个新的顺序表,存放A中所有不为x的元素,T(n) = O(n),S(n) = O(n),空间复杂度不符合要求
解法一
设删除A中所有值等于x元素后的顺序表为A1,显然A1是A的一个子集,所以A1可以复用A的空间。
用k记录不为x的元素的位置,遍历线性表
找到一个不等于x的元素就把它移动到下标为k的位置,同时k+1
最后k的值即为所有不等于x的元素的个数,即删除后的线性表的长度。这个算法的思路类似于重新建表

void delnode1(SqList* l, ElemType x) {
int i, k = 0;
for (i = 0; i < l->length; i++) {
if (l->data[i] != x) {
l->data[k] = l->data[i];
k++;
}
}
l->length = k;
}
解法二
用k记录顺序表A中等于x的元素个数,一边扫描A一边统计等于x的元素的个数,将不为x的元素前移k个位置,最后修改A的长度
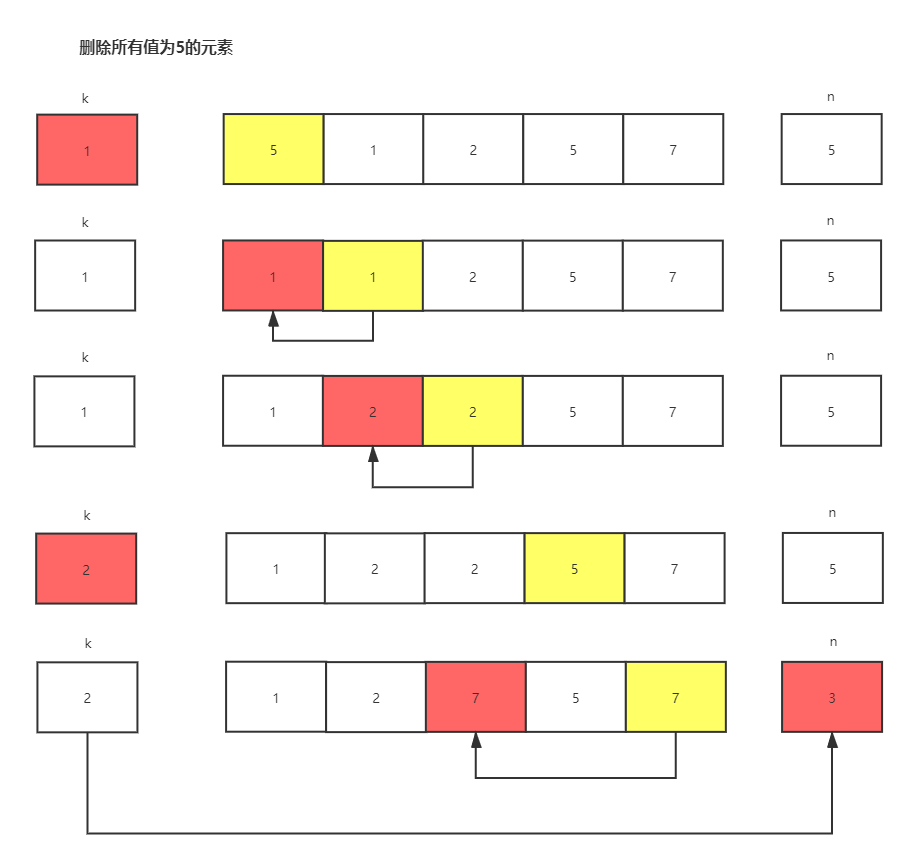
void delnode2(SqList* l, char x) {
int i = 0, k = 0;
while (i < l->length) {
if (l->data[i] == x) {
k++;
}
else {
l->data[i - k] = l->data[i];
}
i++;
}
l->length -= k;
}
例题2
设顺序表L。设计一个算法,以第一个元素为分界线(基准),将所有小于等于它的元素移到该元素的前面,将所有大于它的元素移到该元素的后面
解法一
设置pivot等于表头元素的值
j从后向前找 ≤pivot的元素i从前向后找 >pivot的元素
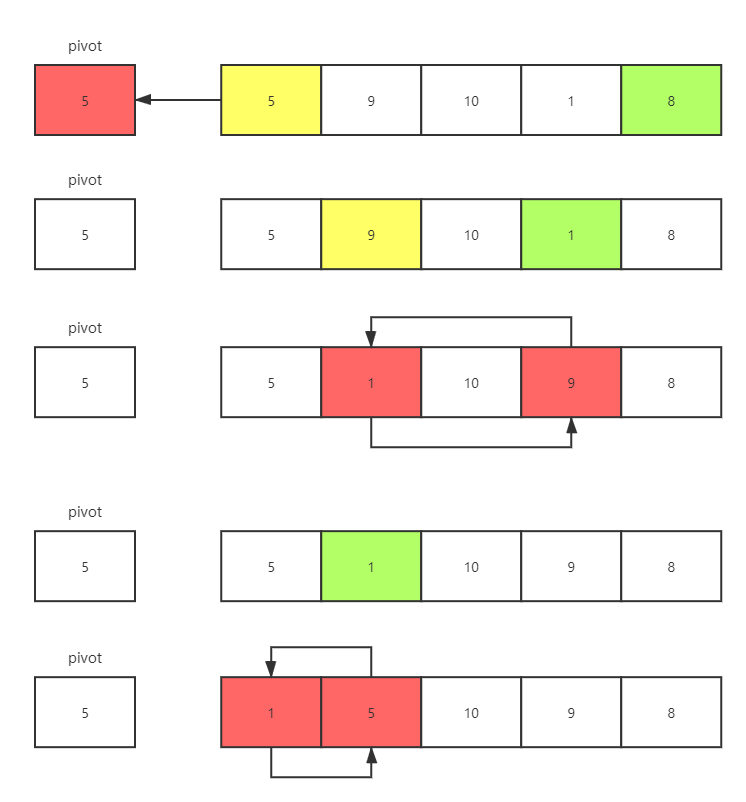
void move1(SqList* l) {
int i = 0, j = l->length - 1;
ElemType pivot = l->data[0];
while (i < j) {
while (i < j && l->data[j] > pivot) {
j--;
}
while (i < j && l->data[i] <= pivot) {
i++;
}
if (i < j) {
swap(&l->data[i], &l->data[j]);
}
}
swap(&l->data[0], &l->data[j]);
}
解法二
j从后向前找 ≤pivot的元素,找到前移i从前向后找 >pivot的元素,找到后移
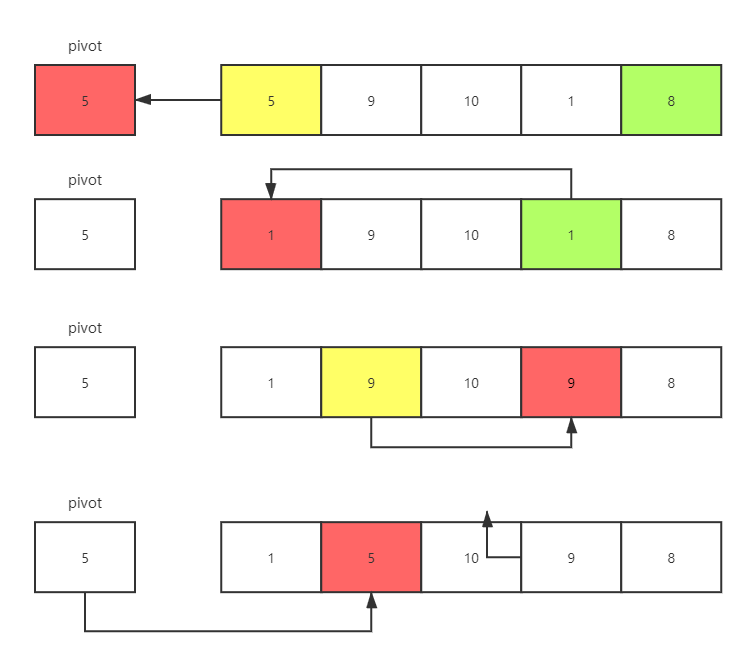
void move2(SqList* l) {
int i = 0, j = l->length - 1;
ElemType pivot = l->data[0];
while (i < j) {
while (j > i && l->data[j] > pivot) {
j--;
}
l->data[i] = l->data[j];
while (i < j && l->data[i] <= pivot) {
i++;
}
l->data[j] = l->data[i];
}
l->data[i] = pivot;
}
荷兰国旗问题

采用顺序表的数据结构存储一个只以0,1,2组成的数字序列,下面的表格是数字的含义
| 红色 | 白色 | 蓝色 |
|---|---|---|
| 0 | 1 | 2 |
请设计一个时间复杂度为O(n)的算法,使得该序列按红白蓝的顺序排号,即排成荷兰国旗的图案
void flag(SqList* l) {
int i = -1, j = 0, k = l->length;
while (j < k) {
if (l->data[j] == 0) {
i++;
swap(&l->data[i], &l->data[j]);
j++;
}
else if (l->data[j] == 2) {
k--;
swap(&l->data[k], &l->data[j]);
}
else {
j++;
}
}
}
顺序表的优劣
| 优点 | 缺点 |
|---|---|
| 存储密度大 | 插入和删除需要移动大量元素 |
| 具有随机存取性 | 初始空间大小分配难以掌握 |
参考链接
https://www.icourse163.org/learn/WHU-1001539003?tid=1002049010#/learn/content?type=detail&id=1002711867&cid=1003019730


 浙公网安备 33010602011771号
浙公网安备 33010602011771号