顺序栈

栈的定义

栈是一种只能在一端进行插入或删除操作的线性表

• 允许进行插入、删除操作的一端称为栈顶
• 表的另一端称为栈底
• 当栈中没有数据元素时，称为空栈
• 栈的插入操作通常称为进栈或入栈
• 栈的删除操作通常称为退栈或出栈

栈的主要特点是后进先出（Last In First Out），即后进栈的元素先出栈，栈也称后进先出表（LIFO表）

进栈出栈的变化形式

栈对线性表的插入和删除的位置进行了限制，并没有对元素进出的时间进行限制，也就是说进栈和出栈的操作是可以交替进行的，只要保证是栈顶的元素就可以出栈。
以下面的输入顺序为例
$$1,2,3$$
第一种情况：输出321

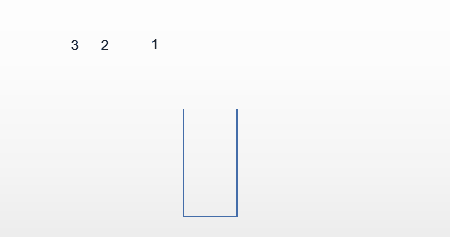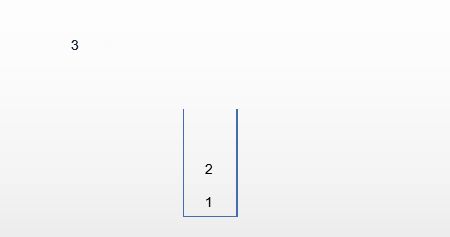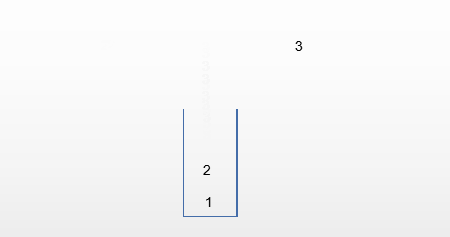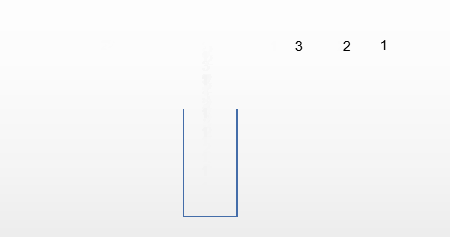
第二种情况：输出123

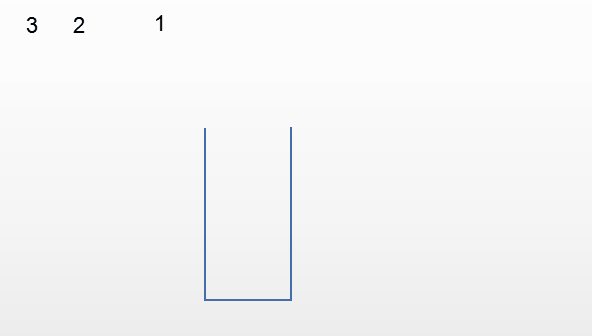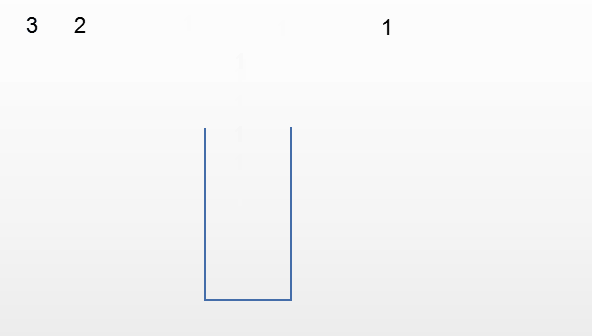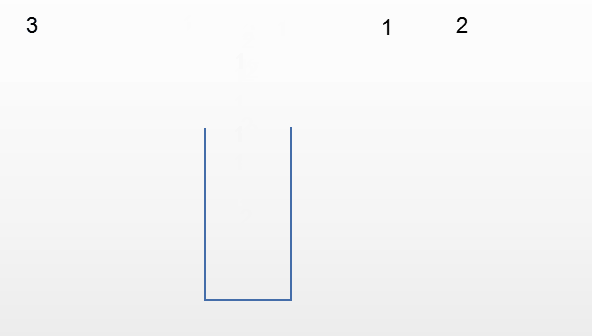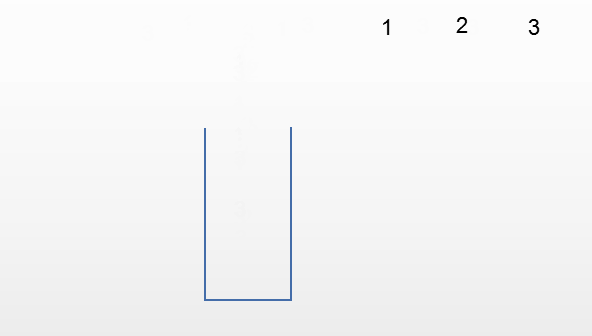
第三种情况：输出213

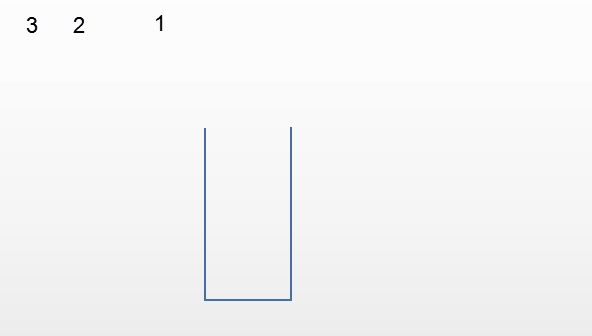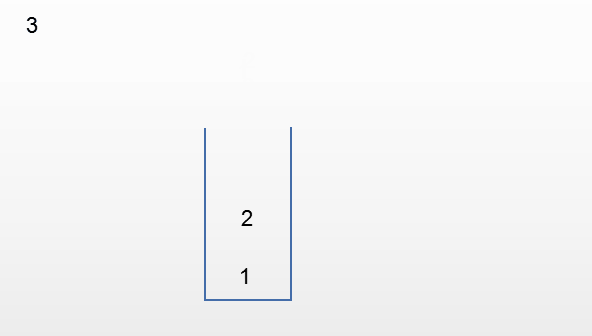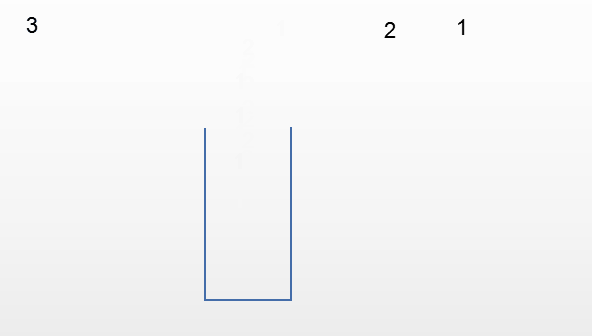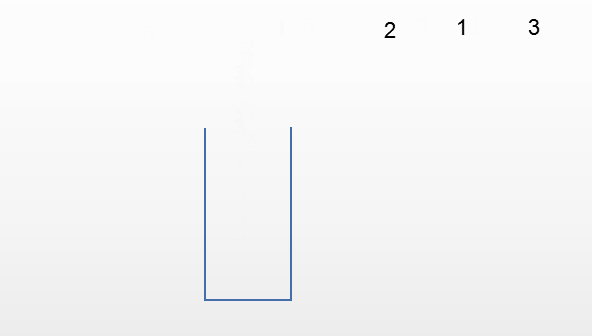
第四种情况：输出132

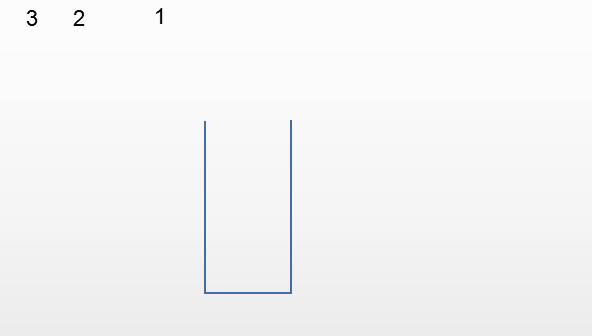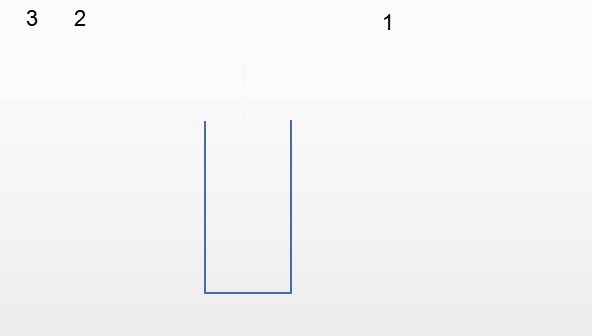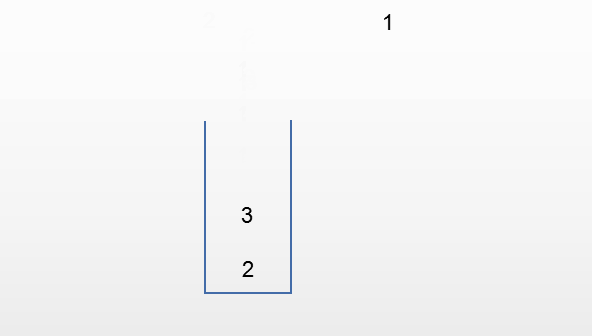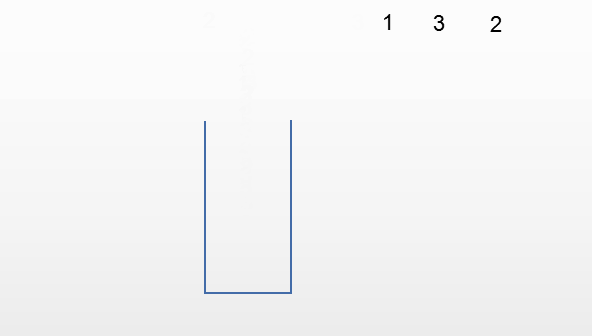
第五种情况：输出231

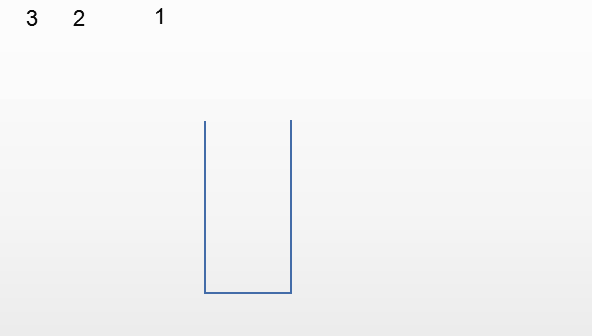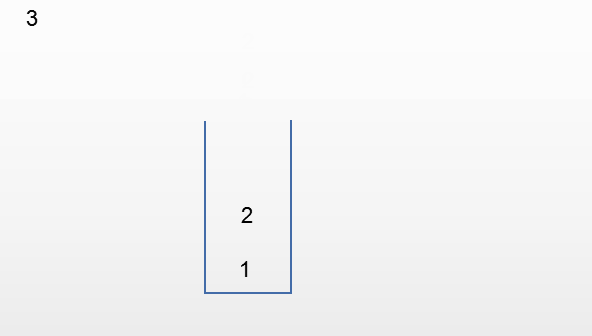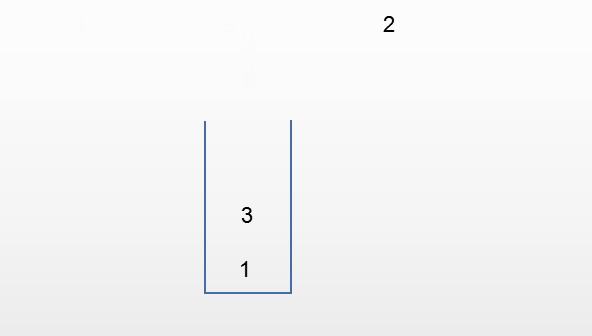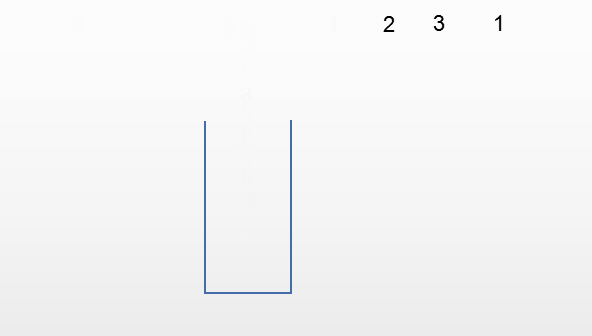
按照排列组合的公式，3个元素应该有6种排列形式
$$A_3^3=3!=6$$
还有一种排列情况是312，这种情况有没有可能呢？
显然，当第一个出栈元素是3的时候，1被2压住了，1不可能是第二个出栈的元素，所以不存在312这种输出结果。

$$\begin{gathered} 出栈序列的个数计算公式 \\ Catalan数 \\ \frac{1}{n+1}{C}_{2n}^n=\frac{1}{n+1}\times \frac{(2n)!}{n!\times n!} \end{gathered}$$

例1

设一个栈的输入序列为a,b,c,d，栈的输出序列不可能是
A. c,d,b,a
B. d,c,b,a
C. a,c,d,b
D. d,a,b,c

比较难想象的是A和C

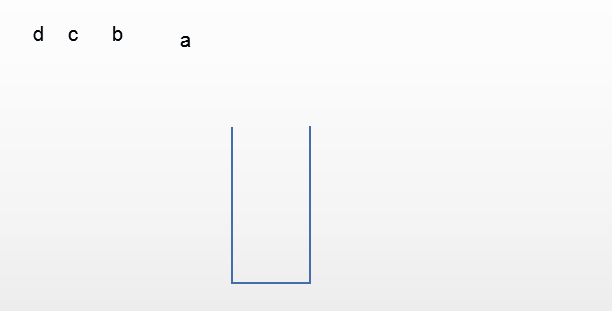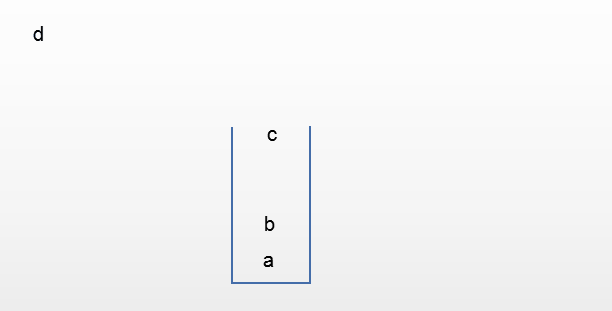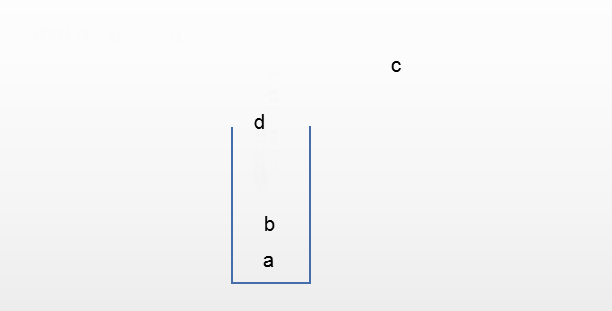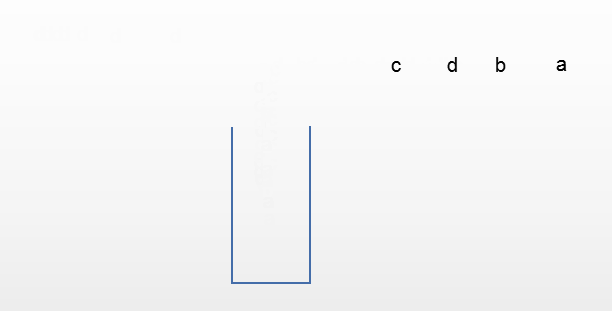
对于D来说，如果先出去的是d，这意味这a和b都被c堵着，没办法先出，所以D的输出顺序是不可能的。

例2

一个栈的入栈序列为1,2,3,…,n，其出栈序列是p1,p2,p3,…,pn。若p1 = 3，则p2可能取值的个数是

显然这道题目中，进栈的同时也会出栈，先按照1,2,3的顺序进栈，然后3出栈，后面的操作，可能是

• 2出栈，1种可能
• 新的元素进栈后出栈（n - 3种可能）

3已经出栈了，减去
1被2压住，没办法第二个出栈
所以可能性是n-2

栈的顺序存储结构

typedef struct _sqStack{
	ElemType data[ MAX_SIZE ];
	int top;
}sqStack;

用数组作为栈的空间，top指向了栈顶的位置

• 建立一个空栈时，top初始化为-1
• 当top == MAX_SIZE - 1时，栈满
• 进栈top++，出栈top--

顺序栈的基本运算

初始化栈

void
initStack( sqStack **s )
{
	*s = ( sqStack* )malloc( sizeof( sqStack ) );
	(*s)->top = -1;
}

销毁栈

void
destroyStack( sqStack *s )
{
	free( s );
}

判断栈是否为空

int
stackEmpty( sqStack *s )
{
	return ( s->top == -1 );
}

进栈

先判断栈是否为满，为满返回FALSE，还有空间时，让top指向下一个位置，将新元素压入栈，返回TRUE

#define TRUE	1
#define FALSE	0

int
push( sqStack *s, int e )
{
	if( s->top == MAX_SIZE - 1 ){
		return FALSE;
	}
	s->data[ ++s->top ] = e;

	return TRUE;
}

出栈

先判断栈是否为空，为空返回FALSE，不为空把栈顶元素取出并弹出，返回TRUE

#define TRUE	1
#define FALSE	0

int
pop( sqStack *s, int *e )
{
	if( s->top == -1 ){
		return FALSE;
	}
	*e = s->data[ s->top-- ];

	return TRUE;
}

取栈顶元素

先判断栈是否为空，为空返回FALSE，不为空把栈顶元素取出，返回TRUE

#define TRUE	1
#define FALSE	0

int
getTop( sqStack *s, int *e )
{
	if( s->top == -1 ){
		return FALSE;
	}
	*e = s->data[ s->top ];
	
	return TRUE;
}

两栈共享空间

要实现两个相同类型的栈，最简单粗暴的方法就是分别做两个数组，还有一种比较巧妙的方法是让两个栈共用一个空间，即在一个数组中存储两个栈。

两个栈从两端向中间生长，只要它们两个不相遇，栈就可以一直使用。

typedef struct _dsqStack{
	ElemType data[ MAX_SIZE ];
	int top1;
	int top2;
}dsqStack;

top1指向了栈1的栈顶，top2指向了栈2的栈顶

• 建立一个空栈时，top1初始化为-1，top2初始化为MAX_SIZE
• 栈1进栈top1++，出栈top1--
  栈2进栈top2--，出栈top2++
• 当top2 - top1 == 1，两个栈都满

初始化

void
initDstack( dsqStack **s )
{
	*s = ( dsqStack* )malloc( sizeof( dsqStack ) );
	(*s)->top1 = -1;
	(*s)->top2 = MAX_SIZE;
}

进栈

int
push( dsqStack *s, int stack_tag, int e )
{
	if( 1 == s->top2 - s->top1 ){
		return FALSE;
	}
	if( 1 == stack_tag ){
		s->data[ ++s->top1 ] = e;
	}else{
		s->data[ --s->top2 ] = e;
	}

	return TRUE;
}

出栈

int
pop( dsqStack *s, int stack_tag, int *e )
{
	if( 1 == stack_tag ){
		if( -1 == s->top1 ){
			return FALSE;
		}else{
			*e = s->data[ s->top1-- ];
		}
	}else{
		if( MAX_SIZE == s->top2 ){
			return FALSE;
		}else{
			*e = s->data[ s->top2++ ];
		}
	}

	return TRUE;
}

栈的应用：判断回文序列

	int i;
	int flag = TRUE;
	char str[] = "AGCTTCGA";
	const char *info[] = { "NO", "YES" };

	sqStack *s;
	initStack( &s );

	for( i = 0; i < strlen( str ); i++ ){
		if( push( s, str[i] ) == FALSE ){
			printf("栈上溢出");
			break;
		}
	}

	for( i = 0; i < strlen( str ); i++ ){
		char temp;
		if( pop( s, &temp ) == FALSE ){
			printf("栈下溢出");
			break;
		}
		if( str[i] != temp ){
			flag = FALSE;
			break;
		}
	}
	printf("%s\n", info[ flag ] );