图的存储结构

图是由顶点集合和边集合组成的，考虑怎么把这两样东西存储在计算机内存中

邻接矩阵

用两个数组来表示图。

• 一个一维数组存储图中顶点信息；
• 一个二维数组，称为邻接矩阵，用来存储图中的边或弧的信息。

无向图

设图G有n个顶点，则邻接矩阵arc是一个n × n的方阵

• 若(vi, vj)∈E，arc[i][j] = 1
• 否则，arc[i][j] = 0
  
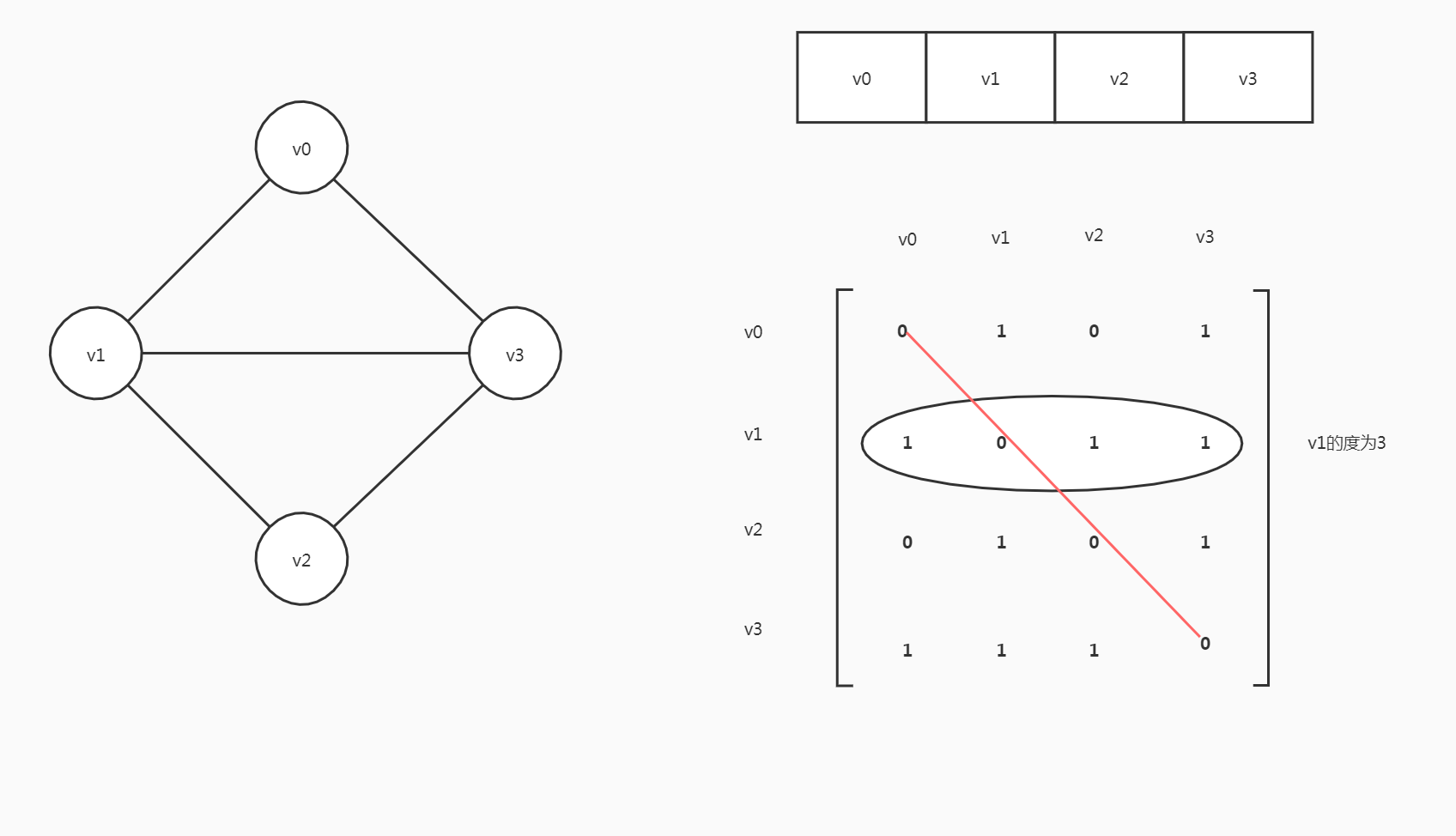
  由于图中不存在自回路，所以邻接矩阵的主对角线，也就是arc[0][0]，arc[1][1]，arc[2][2]，arc[3][3]都是0

同时这个邻接矩阵是一个对称矩阵。

• 例如v1到v3有一条边，arc[1][3] = 1；
• 对应的v3到v1也有一条边，arc[3][1] = 1
  对于邻接矩阵都有arc[i][j] = arc[j][i]

求图中顶点的基本信息

1. 顶点vi和vj之间的边(vi, vj)是否存在，判断arc[i][j]是否为1
2. 求顶点vi的度，对矩阵第i行(或第i列)求和，v1的度即为1+0+1+1=3
3. 求顶点vi的所有邻接点，扫描矩阵第i行，若arc[i][j]为1即为邻接点

有向图

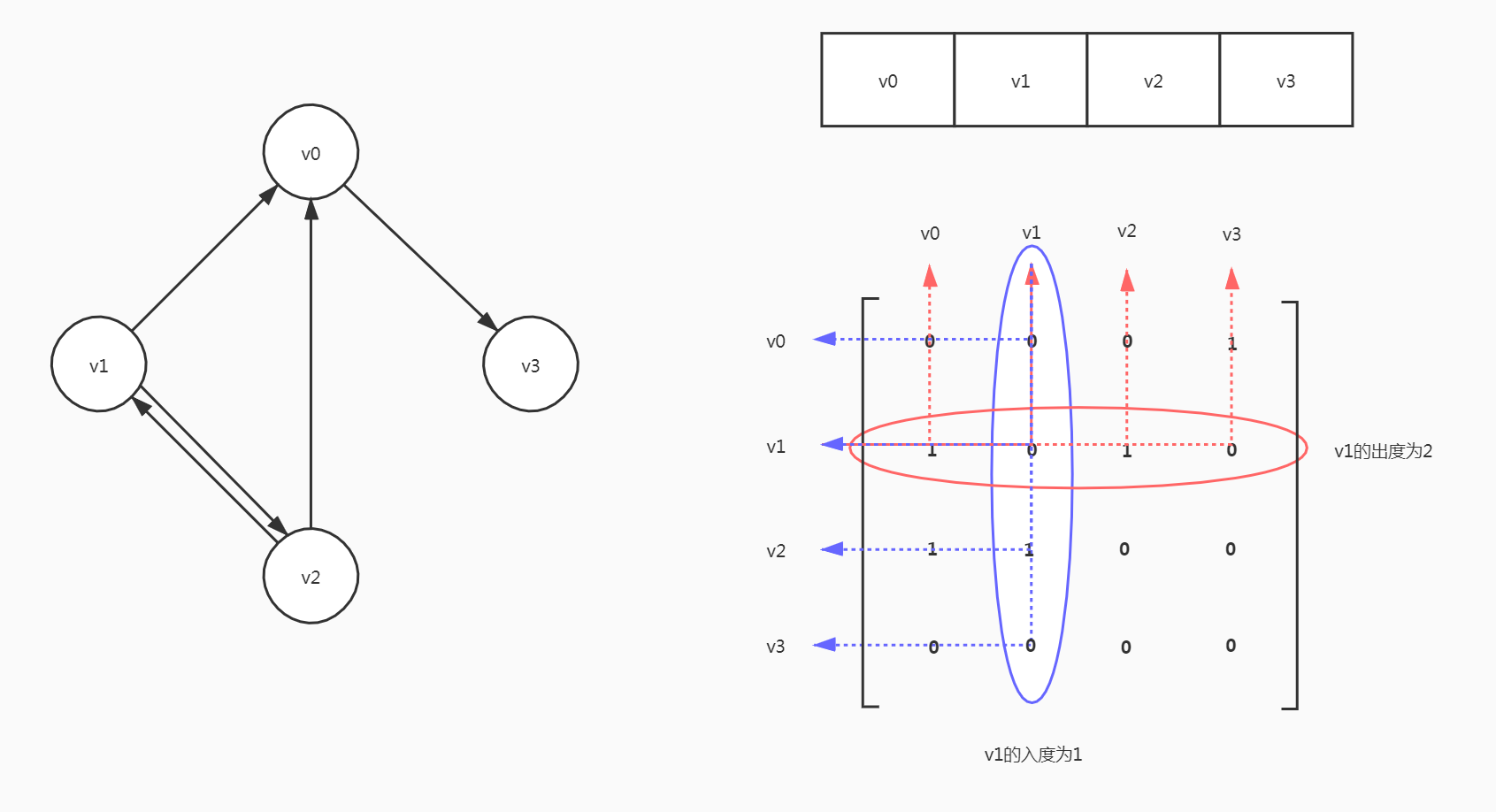
有向图的邻接矩阵的主对角线也是0

有向图讲究入度和出度，所以对应的邻接矩阵不是对称矩阵。

• 例如v0到v3有弧，arc[0][3]=1
• 但v3带v0没有弧，arc[3][0] = 0

求图中顶点的基本信息

1. 顶点vi到vj的弧<vi, vj>是否存在，判断arc[i][j]是否为1
2. 求顶点vi的度，对矩阵第i行求和，再对第i列求和，两次求和结果相加得到结果。
3. 求顶点vi的所有邻接点，扫描矩阵第i行和第i列，若为1即为邻接点

网

每条边上带有权重的图叫做网，这些权重需要一并存储。

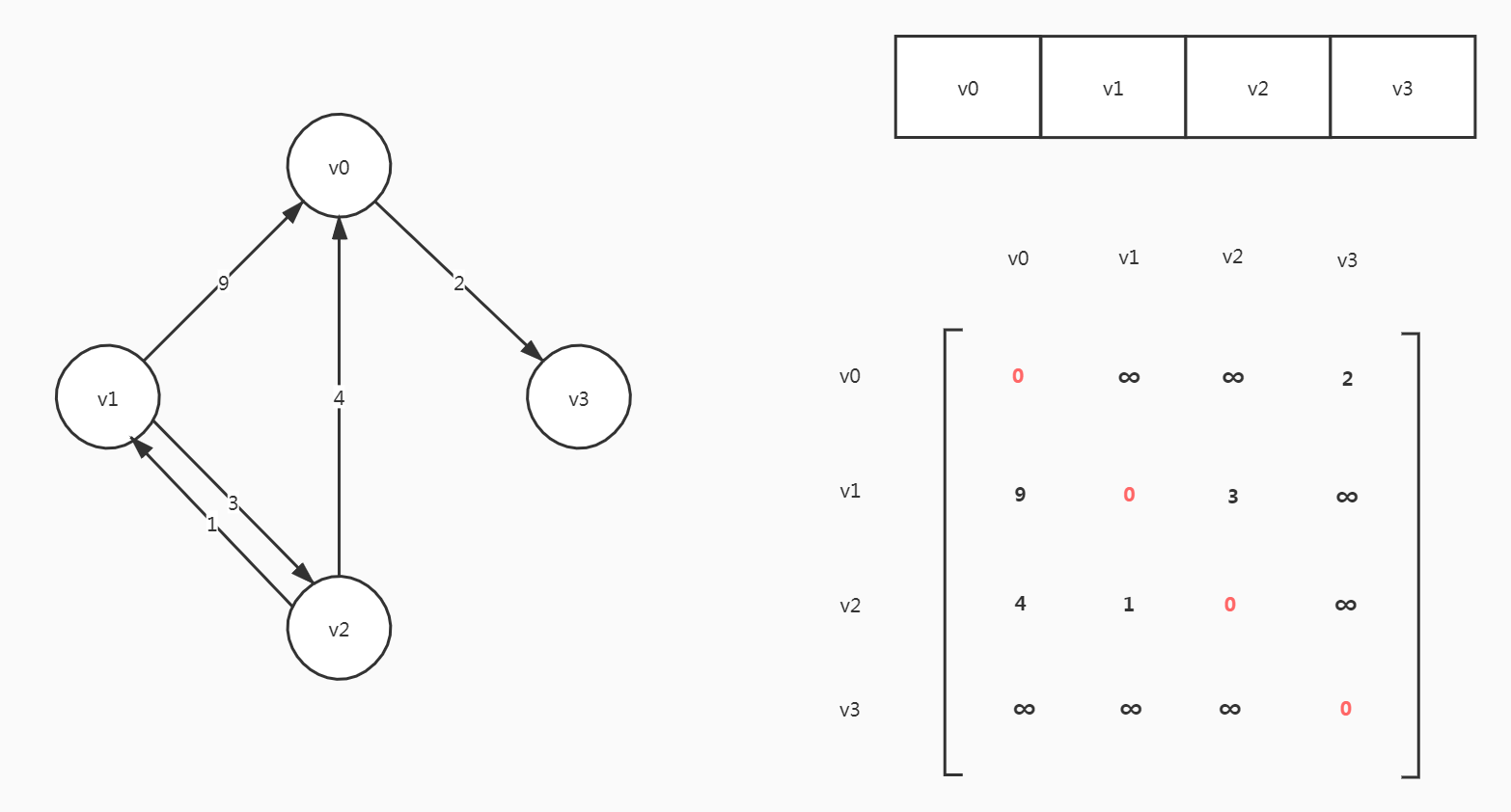
• 当(vi, vj)∈E或<vi, vj>∈E，arc[i][j]=Wij
• 当i=j，arc[i][j] = 0
• 其他情况，arc[i][j] = ∞

wij表示权重，∞用来代表没有边的情况。

typedef int  VertexType;	//顶点类型, 假定为int
typedef char ArcType;		//边的类型, 假定为char

typedef struct _mgraph {
    VertexType* vexs;   //顶点数一维组
    ArcType** arc;      //邻接矩阵
    int num_vexs;       //顶点数目
}mgraph;

void initGraph(mgraph** g)
{
    int i;
    *g = (mgraph*)malloc(sizeof(mgraph));
    printf("输入顶点数\n");
    scanf("%d", &(*g)->num_vexs);

    (*g)->vexs = (VertexType*)malloc(sizeof(VertexType) * (*g)->num_vexs);

    (*g)->arc = (ArcType**)malloc(sizeof(ArcType*) * (*g)->num_vexs);       
    for (i = 0; i < (*g)->num_vexs; i++) {
        (*g)->arc[i] = (ArcType*)malloc(sizeof(ArcType) * (*g)->num_vexs);
    }
}


void createGraph(mgraph* g)
{
    int i, j;
    printf("从0开始按照编号顺序输入顶点值\n");
    for (int i = 0; i < g->num_vexs; i++) {
        scanf("%d", &g->vexs[i]);
    }
    getchar();
    printf("输入邻接矩阵, 矩阵元素之间不要有空格, 用#代替无穷大\n");
    for (i = 0; i < g->num_vexs; i++) {
        for (j = 0; j < g->num_vexs; j++) {
            scanf("%c", &g->arc[i][j]);
        }
        getchar();
    }
}

邻接矩阵的特点

1. 图的邻接矩阵的表示是唯一的
2. 无向图的邻接矩阵一定是一个对称矩阵，可以压缩存储
3. 比较适合存储稠密图，如果存储稀疏图，矩阵中的元素存在很大的浪费
4. 用邻接矩阵存储图，很容易确定任意两个顶点之间是否有边相连（数组的随机存储特性）。但要确定某个顶点的度，就必须按行、按列遍历矩阵，耗时大

无向图邻接矩阵的压缩存储

已知无向图邻接矩阵是一个对称矩阵，只需要存储上三角或下三角即可。以存储下三角为例。
对于一个n*n的矩阵，压缩后元素个数为
$$\frac{(n+1)n}{2}$$

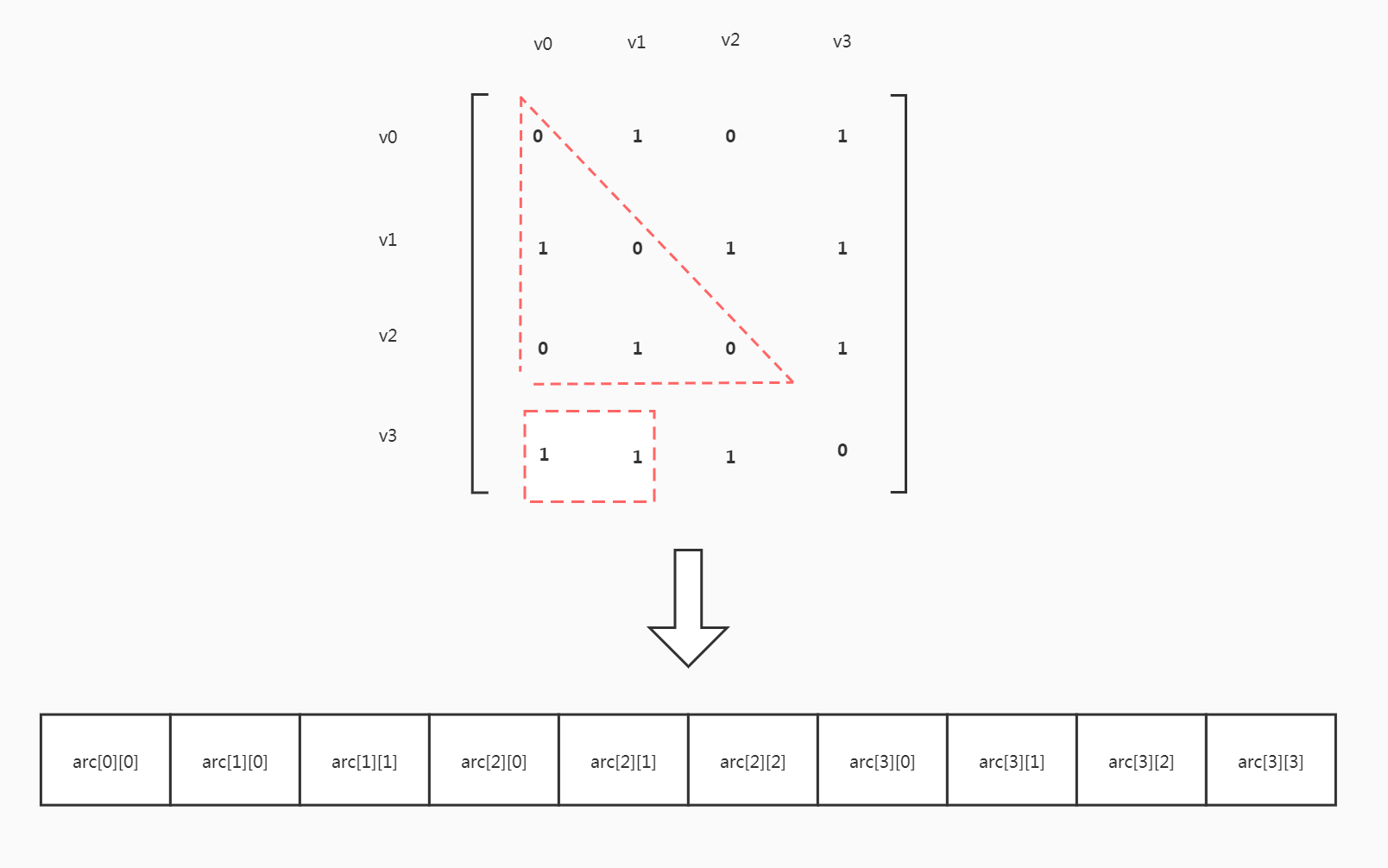
现在要在压缩后的矩阵中访问arc[i][j]，对应的下标是
$$\frac{(i+1)i}{2}+j$$
以arc[3][1]为例，上面i行总共有
$$\frac{(1+3)3}{2}=6个元素$$

再加上j，得到下标为7

下三角的元素满足 i >= j，如果要访问上三角部分，交换i和j即可

邻接表

图的邻接表存储方法将顺序存储结构和链式存储结构相结合

• 给每个顶点建立一个单链表，将顶点i的所有邻接点串起来
• 单链表的头结点放顶点信息，所有的头结点构成一个数组，数组中下标为i的元素表示顶点i的表头节点。

无向图

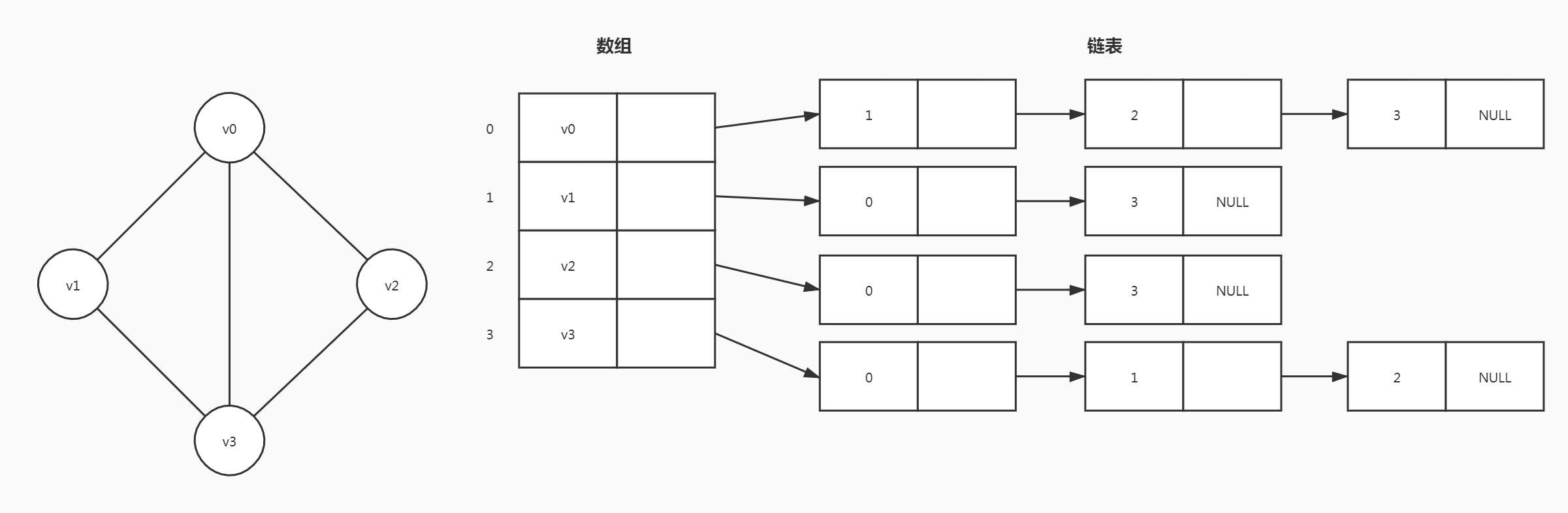
求图中顶点的基本信息

1. 顶点vi到vj的弧<vi, vj>是否存在，在下标为i的位置进入链表查找是否有j
2. 求顶点vi的度，计算对应链表的结点数
3. 求顶点vi的所有邻接点，将对应链表逐个输出

有向图

和无向图不同的是，有向图的边是有方向的，将入度和出度分开存储。

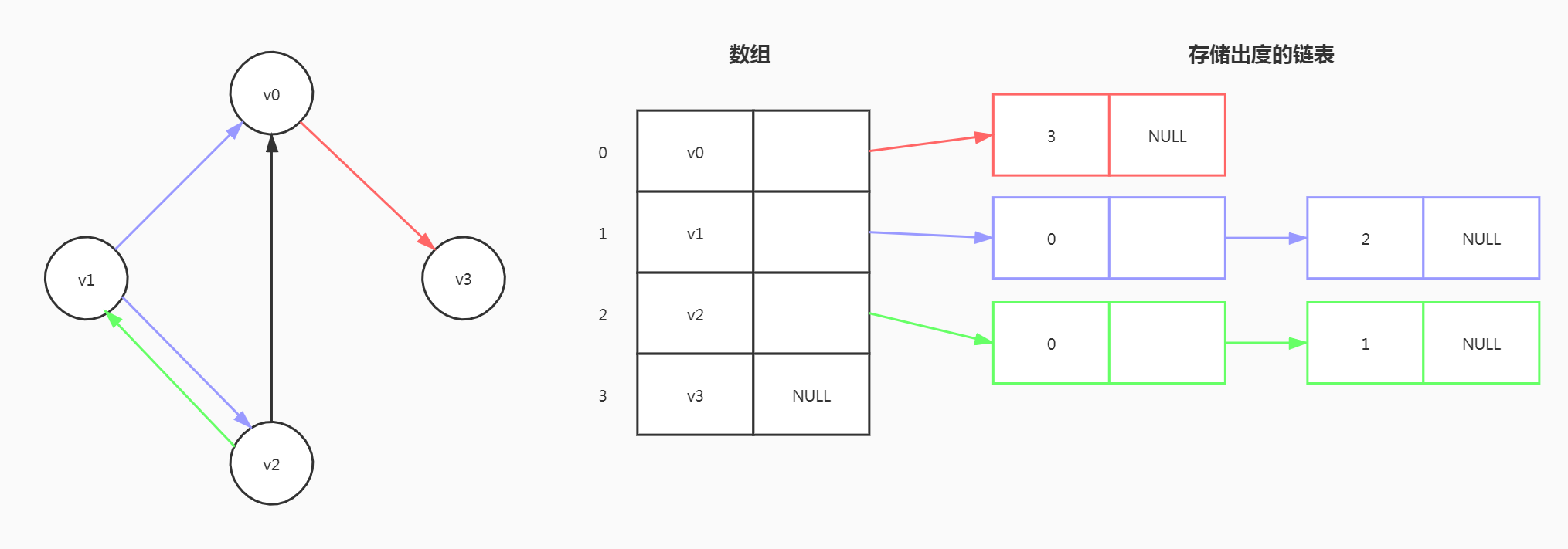
如果上面的结构叫邻接表，那么下面的结构就叫逆邻接表

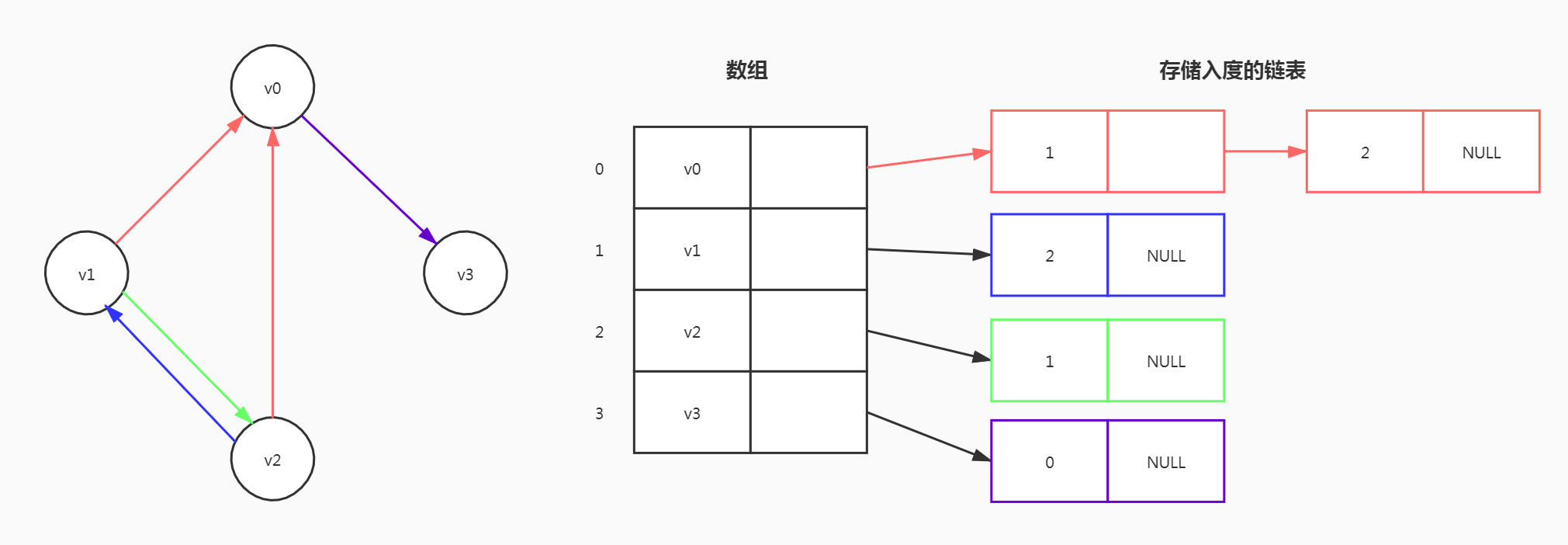
网

在链表节点中增加权重数据域

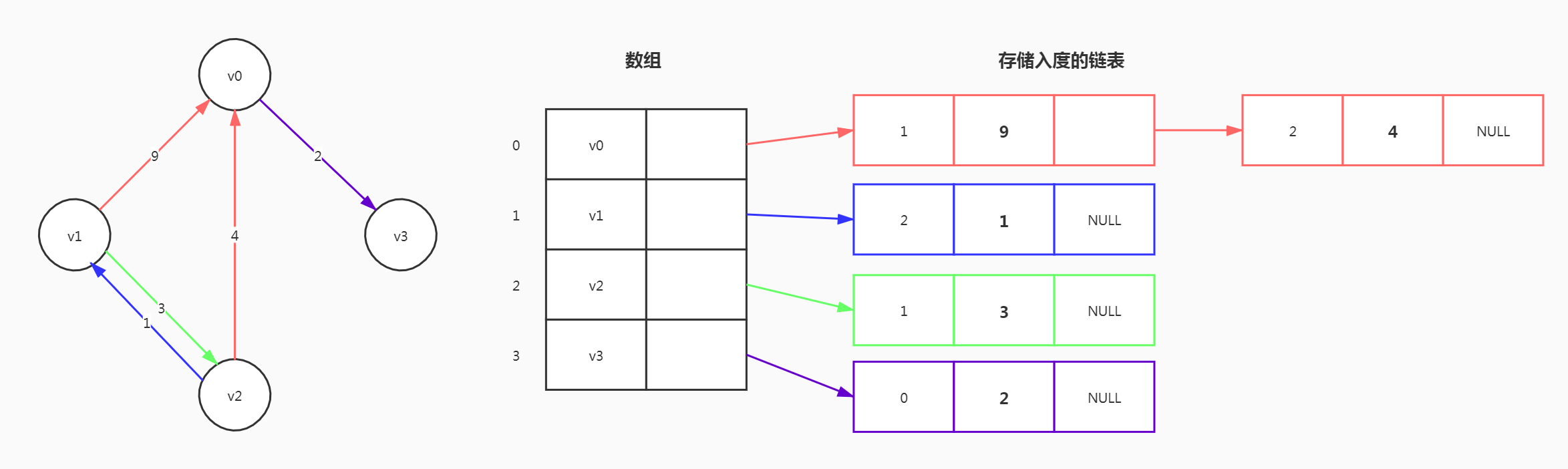
typedef int  VertexType;//顶点类型 假定为int
typedef char ArcType;   //边的类型 假定为char

typedef struct _arcnode {
    int adjvex;         //邻接点下标
    int weight;	        //权重
    struct _arcnode* next;
}arcnode;

typedef struct _vertexnode {
    VertexType data;    //存储顶点信息
    arcnode* head;      //指向邻接表表头的指针
}vertexnode;

typedef struct _Lgraph {
    vertexnode* arr;    //顶点数组
    int num_vexs;       //顶点个数
}lgraph;

void initGraph(lgraph** g)
{
    int n;
    *g = (lgraph*)malloc(sizeof(lgraph));
    printf("输入顶点数\n");
    scanf("%d", &n);
    (*g)->num_vexs = n;
    (*g)->arr = (vertexnode*)malloc(sizeof(vertexnode) * n);
}

void createGraph(lgraph* g)
{
    int i;
    arcnode* p, * tail;
    printf("从0开始按照编号顺序输入顶点值\n");
    for (i = 0; i < g->num_vexs; i++) {
        scanf("%d", &g->arr[i].data);
    }
    getchar();
    printf("从0开始按照编号顺序输入邻接表, 所以输入数据都不要用空格分开, 输入#表示当前结点输入完毕\n");
    for (i = 0; i < g->num_vexs; i++) {
        char adj, weight;
        p = (arcnode*)malloc(sizeof(arcnode));
        g->arr[i].head = tail = p;
        while ((adj = getchar()) != '#' && (weight = getchar()) != '#') {
            p = (arcnode*)malloc(sizeof(arcnode));
            p->adjvex = adj - '0';
            p->weight = weight - '0';
            tail->next = p;
            tail = p;
        }
        tail->next = NULL;
        getchar();
    }
}

邻接表的特点

1. 邻接表的表示不唯一
2. 对于有n个顶点和e条边的无向图，其邻接表有n个vertexnode和2e个arcnode
3. 存储稀疏图时比邻接矩阵节省空间
4. 求一个顶点的所有邻接点的操作很方便，遍历对应的链表即可
5. 不方便检查任意一对顶点是否存在边

十字邻接表

为了兼顾出度和入度的问题，十字邻接表将邻接表和逆邻接表结合起来

typedef int VertexType;

typedef struct _arcnode {
    int tailvex, headvex;                     //tail为起点, head为终点
    struct _arcnode* headlink, * taillink;    //headlink指向下一条入边, taillink指向下一条出边
}arcnode;

typedef struct _vexnode {
    VertexType data;                          //顶点数据域
    arcnode* firstin, * firstout;             //firstin入边链表头指针, firstout出边链表头指针
}vexnode;

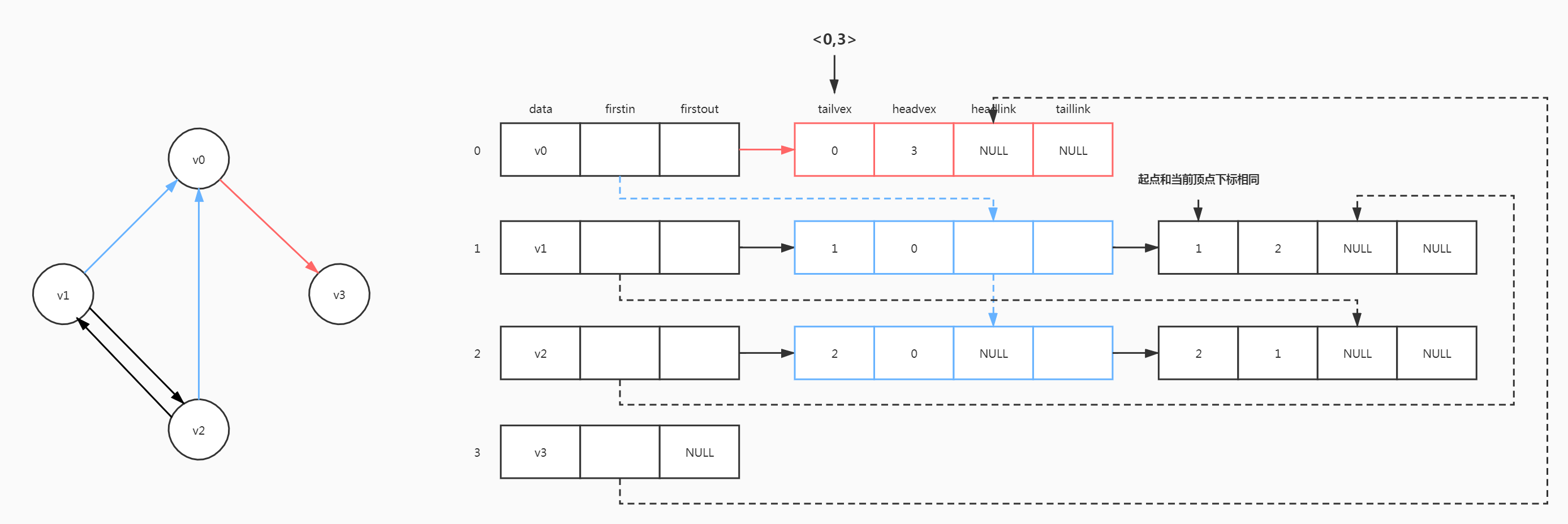
• 找到所有的出边
  从firstout出发，沿着taillink链走，找到<0,3>
• 找到所有的入边
  从firstin出发，沿着headlink链走，找到<1,0>，<2,0>

邻接多重表

邻接多重表用于存储无向图。

在无向图的邻接表存储方法中，每条边(vi, vj)用两个边结点表示。在操作图时带来不便，例如删除某条边时，需要花时间在整个表中找到这两个节点。

typedef int VertexType;

typedef struct _arcnode {
	int ivex;
	struct _arcnode* ilink;
	int jvex;
	struct _arcnode* jlink;
}arcnode;

typedef struct _vexnode {
	VertexType data;
	arcnode* firstedge;
}vexnode;

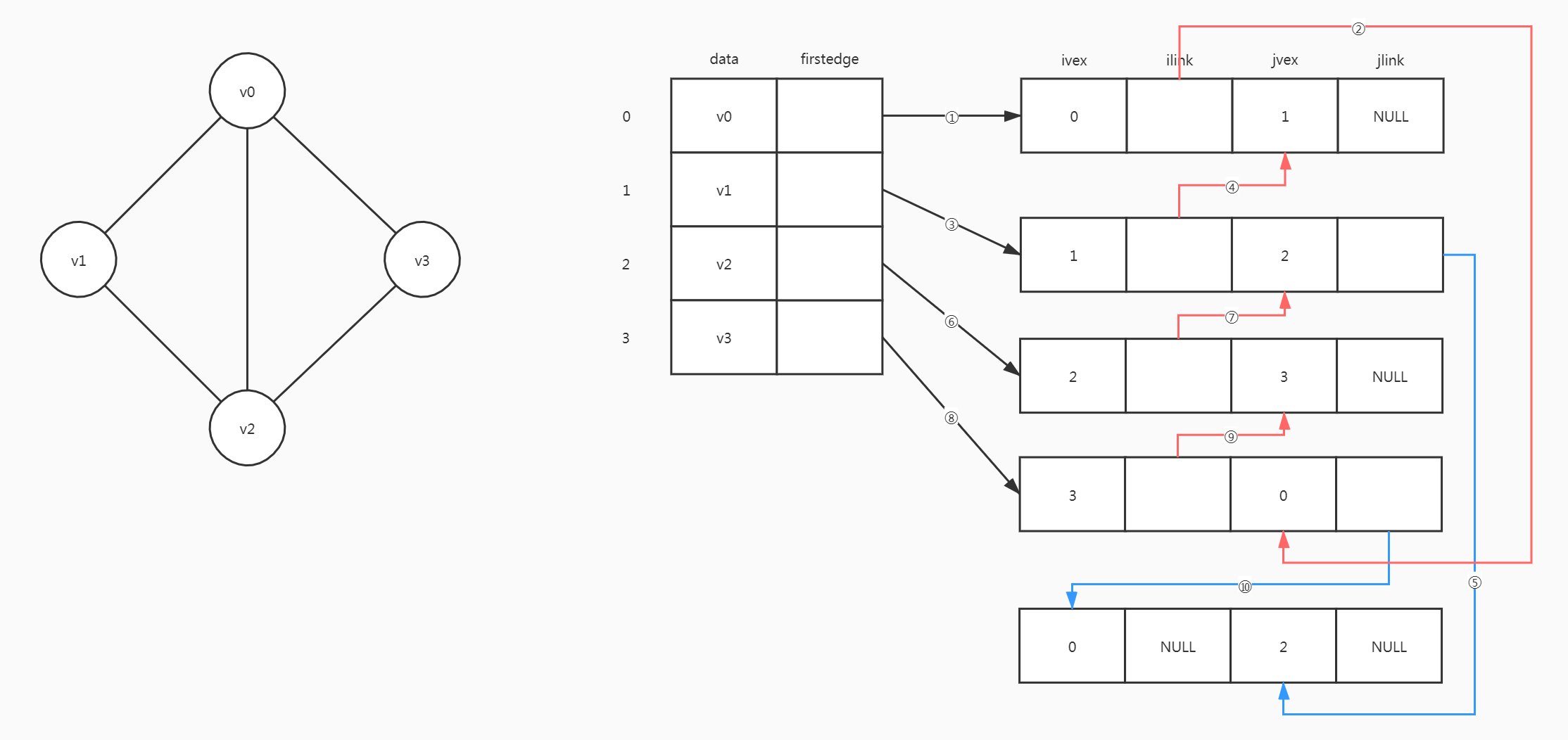
对于邻接多重表而言，所有依附于同一顶点的边串联在同一链表中

找到依附于顶点0的所有边

1. 从下标为0的firstedge出发，找到边(v0, v1)，idex为0，顺着ilink找到下一条边
2. 找到边(v3, v0)，jdex为0，顺着jlink往下找
3. 找到(v0, v2)，idex为0，ilink为NULL，结束

如果要删掉(v0, v2)，只需将图中的⑤和⑩删掉即可。

边集数组

用一个一维数组来存储弧的起点、终点和权重信息。边集数组不适合对顶点相关的操作，它比较适合对边进行处理的操作。

起点	终点	权重

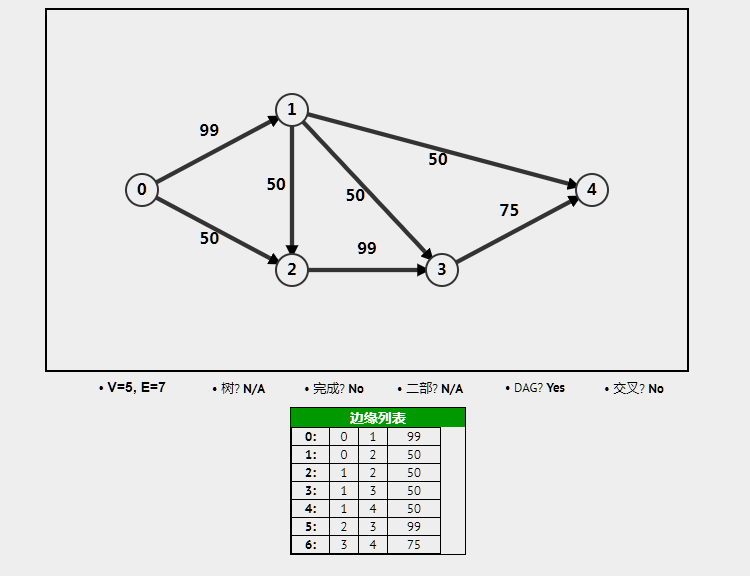
VisuAlgo

可视化的数据结构
https://visualgo.net/zh/graphds