排序

排序

作用：

　　为了将无序的数组变为有序

三种基础排序算法

冒泡：

　　升序（从小到大）：

　　　　原理：

　　　　　　1、从数组的一端开始，将相邻两个元素进行比较，如果前一个元素比后一个元素大，将两个元素进行交换，经过一轮后会找到一个比所有元素都大的元素放在最后

　　　　　　2、接着进行第二轮，重复上述操作，但不用比较最后一个元素，因为最后一个已经是最大值，不用再比较，经过第二轮后找到第二大的元素放在倒数第二的位置

　　　　　　3、继续重复上述操作直到所有元素都在正确的位置，则排序完成

int[] array = {33, 20, 43, 645, 1, 34, 43, 127, 65, 9};
for (int i = 1; i < array.length; i++) {
    for (int j = 0; j < array.length-i; j++) {
        if (array[j] > array[j+1]) {
            int t = array[j];
            array[j] = array[j+1];
            array[j+1] = t;
        }
    }
}

　　降序：

　　　　原理相同，每次比较后将大的元素放在前面

　　理解：

　　　　类似于打擂台，将所有元素都两两比较

　　利：

　　　　操作简单，便于理解

　　弊：

　　　　当数组元素数量多时，比较次数会成倍上升，效率较低

选择：

　　升序：

　　　　原理：

　　　　　　1、假设第一个元素是最大值，记录它的位置，将它和后面的元素依次进行比较

　　　　　　2、当出现比它大的新值时，将新值作为最大值，记录新值的位置，继续向后比较

　　　　　　3、一轮后找到最大值，将最大值放在最后一位，进行值交换（如果最大值就是最后一位，则不进行交换）

　　　　　　4、重复上述操作，寻找第二大的值，且不用和最后一位值进行比较，直到所有元素都在自己的位置，则排序完成

int[] array = {115, 82, 110, 8, 102, 11, 51, 31, 13, 60};
for (int i = 0, max, max_p; i < array.length; i++) {
    max_p = array.length-1-i;
    max = 0;
    for (int j = 1; j <= max_p; j++) {
        if (array[j]>array[max]) {
            max = j;
        }
    }
    if(max_p != max){
        int t = array[max_p];
        array[max_p] = array[max];
        array[max] = t;
    }
}

　　降序：

　　　　原理相同，将第一个数定为最小值，比较有没有比它更小的值，一轮后放再最后

　　理解：

　　　　和冒泡排序相似，都是比较排序，但是在比较的基础上，选择排序只是记住位置再交换，交换次数远小于冒泡排序，所以节省了时间消耗

　　利：

　　　　操作简单，便于理解

　　弊：

　　　　虽然在冒泡排序的基础上减少的交换次数，但是元素数量多时依旧会有大量比较和交换操作，效率低

插入：

　　升序：

　　　　原理：

　　　　　　1、将元素划分成两个部分，左侧有序，右侧无序

　　　　　　2、从左侧开始，将元素依次进行比较，当出现右侧元素比左侧元素小，记录下右侧元素的值，将左侧比该元素大的元素依次向右移动一位，直到出现比该元素小或达到数组边界，将该元素插入左侧元素中

　　　　　　3、重复上述操作，当右侧元素全部插入左侧元素中时，数组整体有序，则排序完成

int[] array = {115, 82, 110, 8, 102, 11, 51, 31, 13, 60};
for (int i = 1; i < array.length; i++) {
    if (array[i]>=array[i-1]) {
        continue;
    }
    int t = array[i];
    int j;
    for (j = i-1; j >= 0 && array[j]>t ; j--) {
        array[j+1] = array[j];
    }
    array[j+1] = t;
}

 　　降序：

　　　　将左侧降序，当右侧元素大于左侧元素时插入，并找到比右侧元素大的元素或数组边界为止

　　理解：

　　　　将数组绝对无序变为局部有序，将局部有序扩大到整体有序的过程，相对于选择排序，平均交换比较次数小，并且在数据类型简单的情况下，插入排序通过赋值进行操作的消耗小于选择排序进行值交换的操作，所以数据类型简单的情况插入排序比选择排序平均所耗时间短

　　利：

　　　　在数据类型简单的情况下，平均时间消耗比选择排序短

　　弊：

　　　　当数据类型复杂时，赋值所消耗的时间大

　　

三种高价排序：

高价排序目标：

　　时间小(优先)，空间小

　　无序->相对有序->绝对有序

希尔：

　　升序：

　　　　原理：

　　　　　　1、定义一个步长为数组长度/2

　　　　　　2、依次将元素与相差一个步长位置的元素进行比较，如果前一个元素大于后一个元素，则交换

　　　　　　3、每轮将步长/2，重复上述操作，直到步长<2

　　　　　　4、插入排序

int[] array = {14, 98, 35, 67, 56, 99, 34, 67, 32, 46, 59, 34, 85, 23, 45, 89, 25, 23};
//希尔：将数组变为相对有序
int size = array.length;
while ((size/=2)>=2){
    //步长size
    for (int i = 0; i+size < array.length; i++) {
        if (array[i]>array[i+size]) {
            int t = array[i];
            array[i] = array[i+size];
            array[i+size] = t;
        }
    }
    //插入
    for (int i = 1; i < array.length; i++) {
        int temp = array[i];
        int j;
        for (j = i-1; j >= 0 && array[j]>temp; j--) {
            array[j+1] = array[j];
        }
        array[j+1] = temp;
    }
}

 　　降序：

　　　　相差一个步长的元素进行比较时将小元素放在后面，再将插入排序部分按照降序排序的方式实现

　　理解：

　　　　在插入排序的基础上增加了使数组从无序变为相对有序的操作，使数组整体呈现有序，但没有完全有序，再使用插入排序，将数组变为绝对有序，大大减少了插入排序中循环、数据交换的操作

　　优：

　　　　当数组整体呈现无序时，将数组从无序向局部有序方向变化能大大减少插入排序的消耗

计数：

　　升序：

　　　　原理：

　　　　　　1、声明一个 数组范围为原数组值的范围(最大值-最小值+1) 数组

　　　　　　2、将原数组所有元素减去最小值，那么就可以将元素存储到与元素值相同的下标中，每存储一个元素，新数组+1，用新数组记录原数组每个值的出现次数

　　　　　　3、将新数组下标值加最小值作为元素的值导入覆盖原数组，则排序完成

int max = array[0], min = array[0];
//找元素最大值和最小值
for (int i = 1; i < array.length; i++) {
    if (array[i]>max) {
        max = array[i];
    }
    if (array[i]<min) {
        min = array[i];
    }
}
//定义计数数组
int[] temp = new int[max-min+1];
for(int value:array){
    //利用元素与新数组下标的关系，将原数组数据存储到新数组中
    //新数组的下标表示每个元素的值，新数组的值表示每个元素出现的次数
    temp[value-min]++;
}
//将新数组重新导入到原数组中，因新数组便利的原因，重新导入的元素是有序的
for (int i = 0, k = 0; i < temp.length; i++) {
    for (int j = 0; j < temp[i]; j++) {
        array[k++] = min + i;
    }
}

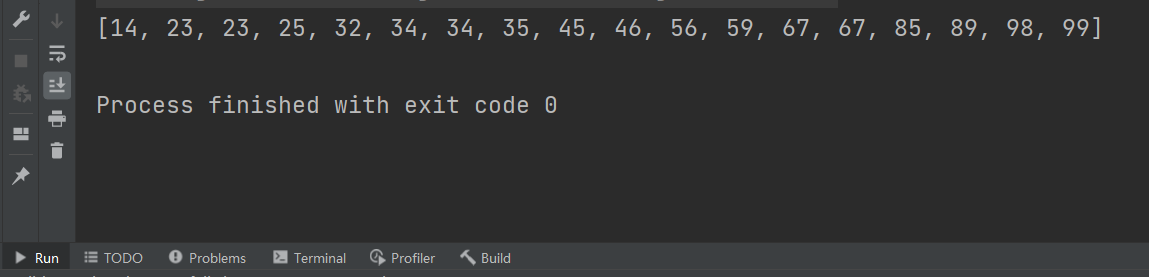
　　降序：

　　　　将新数组按从大到小覆盖原数组即可

　　理解：

　　　　根据数组元素的取值范围创建新数组

　　　　利用元素与下标的关系，将数组的值放在新数组中

　　　　新数组的下标代表数组元素的大小，新数组的值代表元素出现的次数，以此来将原数组全部放入新数组中

　　　　通过下标将元素的值重新放回原数组，因为下标有序，所以返回的元素也有序，所以排序完成

　　优：

　　　　当数组的元素范围小时，创建的新数组容量小，节省空间，因没有大量的比较和交换，节省排序时的时间和空间消耗

基数：

　　顺序：

　　　　原理：

　　　　　　1、找最大位数(最大值的位数)

　　　　　　2、声明一个大小为10的一维数组存储0~9每个位数出现的次数，声明一个外层为10，内层为原数组长度的二位数组，来存储原数组中的数据

　　　　　　3、通过每次循环位数的不同(0~9),将原数组中的值存入二维数组中，并用一维数组记录次数

　　　　　　4、再按照一维数组中记录的次数将存入二维数组的数据覆盖原数组

　　　　　　5、将一维数组清空，并重复上述操作，将每个位数都进行分组排序

//找最大值
int max = array[0];
for (int i = 1; i < array.length; i++) {
    if (array[i]>max){
        max = array[i];
    }
}
//计算最大位数
int size = 1;
while ((max/=10)>=1) {
    size++;
}
//创建数组
int[] ixs = new int[10];
int[][] val = new int[10][array.length];
for (int i = 0, t; i < size; i++){
    //按数位值提取：如个位，十位，百位...
    for(int v : array){
        t = (v/(int)Math.pow(10, i))%10;
        val[t][ixs[t]++] = v;
    }
    //按数位值放回
    for (int j = 0, m = 0; j < ixs.length; j++) {
        for (int k = 0; k < ixs[j]; k++) {
            array[m++] = val[j][k];
        }
    }
    //ixs清零
    for (int j = 0; j < ixs.length; j++) {
        ixs[j] = 0;
    }
}

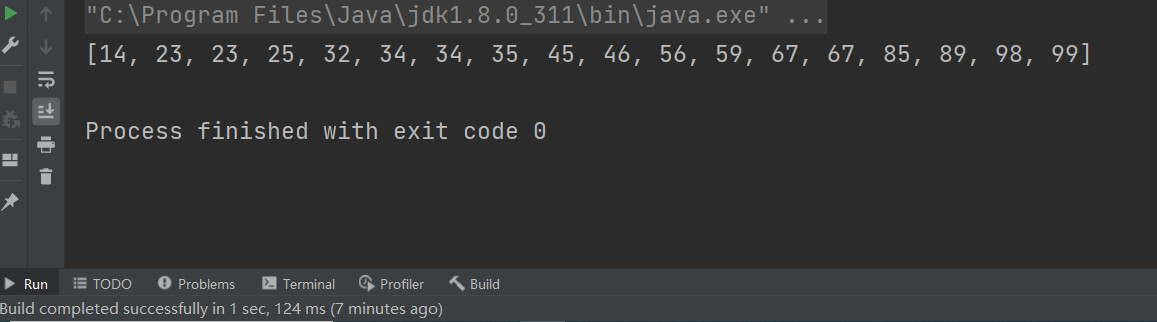
 　　降序：

　　　　将一维数组从大到小放回实现降序

//基数降序
//找最大值
int max = array[0];
for (int i = 1; i < array.length; i++) {
    if (array[i]>max){
        max = array[i];
    }
}
//计算最大位数
int size = 1;
while ((max/=10)>=1) {
    size++;
}
//创建数组
int[] ixs = new int[10];
int[][] val = new int[10][array.length];
for (int i = 0, t; i < size; i++){
    //按数位值提取：如个位，十位，百位...
    for(int v : array){
        t = (v/(int)Math.pow(10, i))%10;
        val[t][ixs[t]++] = v;
    }
    //按数位值放回
    for (int j = ixs.length-1, m = 0; j >= 0; j--) {
        for (int k = 0; k < ixs[j]; k++) {
            array[m++] = val[j][k];
        }
    }
    //ixs清零
    for (int j = 0; j < ixs.length; j++) {
        ixs[j] = 0;
    }
}

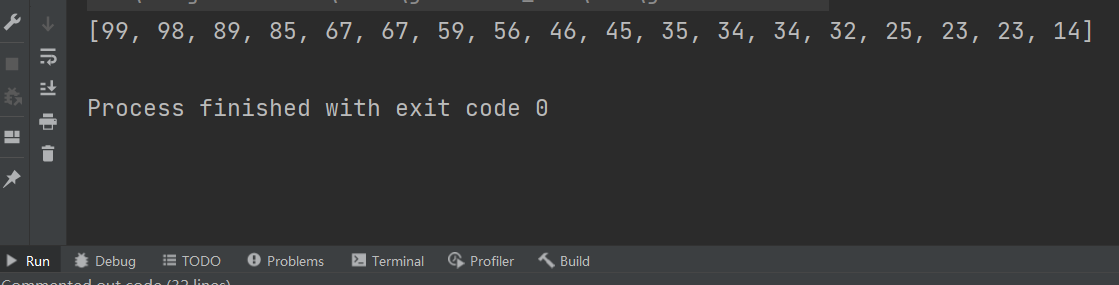
　　理解：

　　　　通过循环，将每次位数(个位，十位，百位...)的值进行排序，当所有位数都相对有序时，整体呈现绝对有序，排序完成

　　优：

　　　　在数组元素的位数范围小时，创建的新二维数组的空间小，节省空间，没有大量比较和交换，节省排序中的消耗