Algorithm - Sortings

测试代码

#include "pch.h"
#include <iostream>
using namespace std;
void Swap(int &a, int &b) {
    int c = a;
    a = b;
    b = c;
}
void Print(int A[], int len) {
    for (int i = 0; i < len; i++) {
        cout << A[i] << " ";
    }
    cout << endl;
}
int main()
{
    int arr[] = { 6, 3, 9, 4, 1, 2, 8, 7, 5 };
    int arr1[] = { 6, 3, 9, 4, 1, 2, 8, 7, 5, 6 };
    int arr2[] = { 11, 13, 51, 34, 12, 0, 8, 7, 5, 13 };

    // Sort();

    Print(arr, 9);
    Print(arr1, 10);
    Print(arr2, 10);
}

冒泡排序

// 分类 -------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- O(n^2)
// 最优时间复杂度 ---- 如果能在内部循环第一次运行时,使用一个旗标来表示有无需要交换的可能,可以把最优时间复杂度降低到O(n)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 稳定
void BubbleSort(int A[], int len) {
    // 每次最大元素就像气泡一样"浮"到数组的最后
    for (int i = len - 1; i > 0; i--){
        // 依次比较相邻的两个元素,使较大的那个向后移
        for (int j = 0; j < i; j++){
            // 如果条件改成A[j] >= A[j + 1],则变为不稳定的排序算法
            if (A[j] > A[j + 1])
                Swap(A[j], A[j + 1]);
        }
    }
}

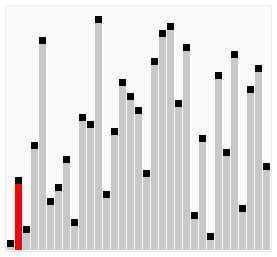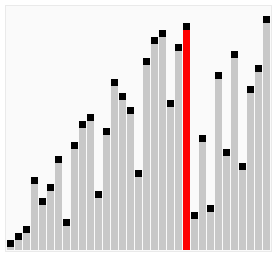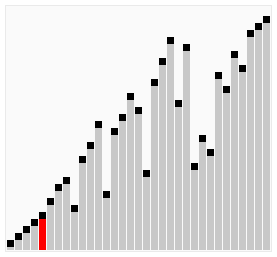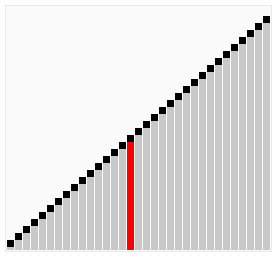
图解:

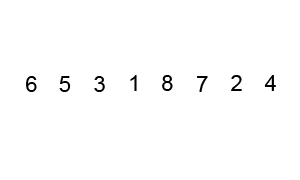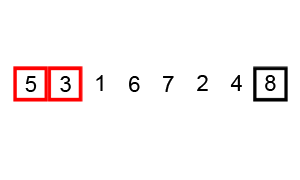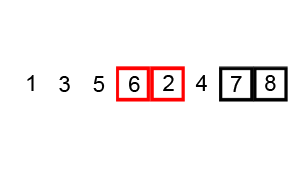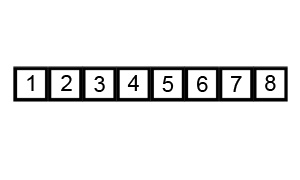
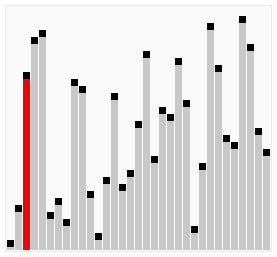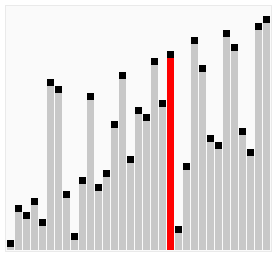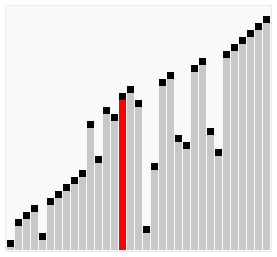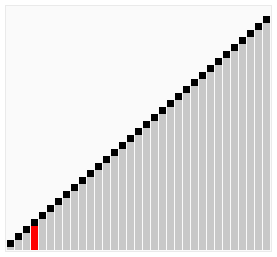
冒泡排序的优化 - 鸡尾酒排序

此算法与冒泡排序的不同处在于从低到高然后从高到低

// 分类 -------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- O(n^2)
// 最优时间复杂度 ---- 如果序列在一开始已经大部分排序过的话,会接近O(n)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 稳定
void CocktailSort(int A[], int len){
    // 初始化边界
    int left = 0;                            
    int right = len - 1;
    while (left < right) {
        // 前半轮,将最大元素放到后面
        for (int i = left; i < right; i++){
            if (A[i] > A[i + 1])
                Swap(A[i], A[i + 1]);
        }
        right--;
        // 后半轮,将最小元素放到前面
        for (int i = right; i > left; i--){
            if (A[i - 1] > A[i]) 
                Swap(A[i - 1], A[i]);
        }
        left++;
    }
}

选择排序

解释:

多次从头遍历到末尾,

每一趟都记下该趟中最小(最大)的元素

此处可以每一趟同时记下最大最小元素, 将其同时对调

速度应该是快2倍

将最小的元素换到指定位置

// 分类 -------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- O(n^2)
// 最优时间复杂度 ---- O(n^2)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 不稳定, 不稳定发生在最小元素与A[i]交换的时刻, 比如序列{5,8,5,2,9} 将2跟第一个5进行置换的时候, 就发生了不稳定现象
void SelectionSort(int A[], int len){
    // i为已排序序列的末尾
    for (int i = 0; i < len - 1; i++){
        int minIndex = i;
        // 未排序序列
        for (int j = i + 1; j < len; j++){ 
            // 找出未排序序列中的最小值
            if (A[j] < A[minIndex])
                minIndex = j;
        }
        if (minIndex != i)
            // 放到已排序序列的末尾，该操作很有可能把稳定性打乱，所以选择排序是不稳定的排序算法
            Swap(A[minIndex], A[i]);
    }
}

图解:

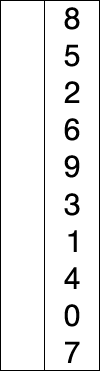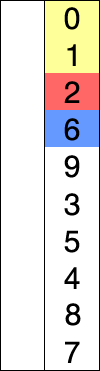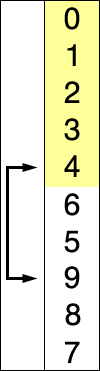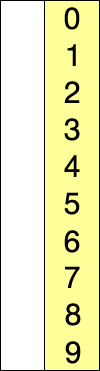
插入排序

// 分类 ------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- 最坏情况为输入序列是降序排列的,此时时间复杂度O(n^2)
// 最优时间复杂度 ---- 最好情况为输入序列是升序排列的,此时时间复杂度O(n)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 稳定
void InsertionSort(int A[], int len){
    // 类似抓扑克牌排序
    for (int i = 1; i < len; i++){
        // 右手抓到一张扑克牌
        int get = A[i];
        // 拿在左手上的牌总是排序好的
        int j = i - 1;
        // 将抓到的牌与手牌从右向左进行比较
        while (j >= 0 && A[j] > get) {
            // 如果该手牌比抓到的牌大，就将其右移
            A[j + 1] = A[j];            
            j--;
        }
        // 直到该手牌比抓到的牌小(或二者相等)，将抓到的牌插入到该手牌右边(相等元素的相对次序未变，所以插入排序是稳定的)
        A[j + 1] = get; 
    }
}

图解:

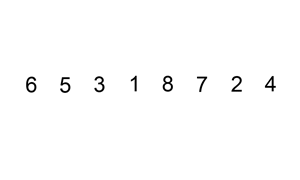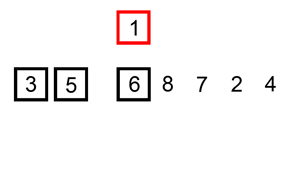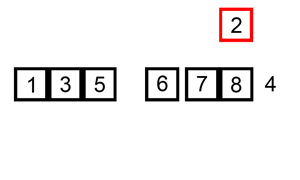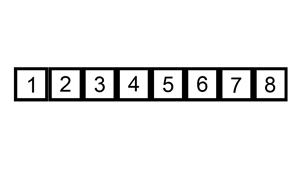
插入排序的改进 - 二分插入排序

// 分类 -------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- O(n^2)
// 最优时间复杂度 ---- O(nlogn)
// 平均时间复杂度 ---- O(n^2)
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 稳定
void InsertionSortDichotomy(int A[], int len) {
    for (int i = 1; i < len; i++) {
        // 右手抓到一张扑克牌
        int get = A[i];
        // 拿在左手上的牌总是排序好的，所以可以用二分法
        int left = 0;
        // 手牌左右边界进行初始化
        int right = i - 1;
        // 采用二分法定位新牌的位置
        while (left <= right) {
            int mid = (left + right) / 2;
            if (A[mid] > get)
                right = mid - 1;
            else
                left = mid + 1;
        }
        // 将欲插入新牌位置右边的牌整体向右移动一个单位
        for (int j = i - 1; j >= left; j--)
            A[j + 1] = A[j];
        // 将抓到的牌插入手牌
        A[left] = get;                    
    }
}

当n较大时，二分插入排序的比较次数比直接插入排序的最差情况好得多，但比直接插入排序的最好情况要差，所当以元素初始序列已经接近升序时，直接插入排序比二分插入排序比较次数少。二分插入排序元素移动次数与直接插入排序相同，依赖于元素初始序列。

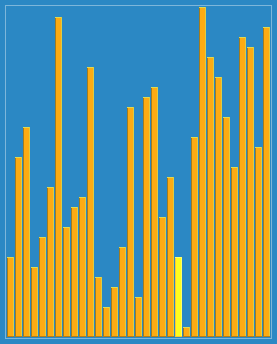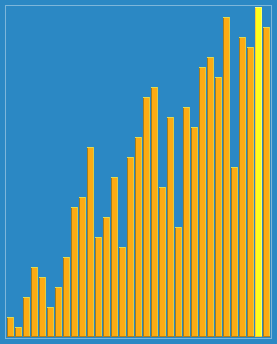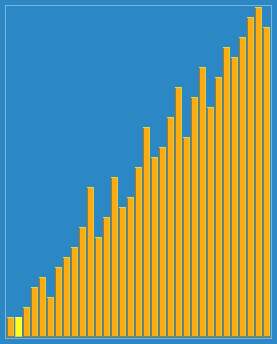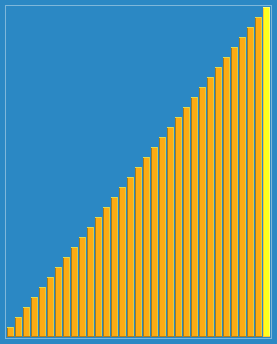
插入排序的更高改进 - 希尔排序

// 分类 -------------- 内部比较排序
// 数据结构 ---------- 数组
// 最差时间复杂度 ---- 根据步长序列的不同而不同。已知最好的为O(n(logn)^2)
// 最优时间复杂度 ---- O(n)
// 平均时间复杂度 ---- 根据步长序列的不同而不同。
// 所需辅助空间 ------ O(1)
// 稳定性 ------------ 不稳定
void ShellSort(int A[], int len) {
    int h = 0;
    // 生成初始增量
    while (h <= len)  h = 3 * h + 1;
    while (h >= 1){
        for (int i = h; i < len; i++){
            int j = i - h;
            int get = A[i];
            while (j >= 0 && A[j] > get) {
                A[j + h] = A[j];
                j = j - h;
            }
            A[j + h] = get;
        }
        // 递减增量
        h = (h - 1) / 3;
    }
}

图解:

归并排序

解释: 归并排序简单的来说就是把一个数组分成两个部分, 然后各自对每个部分执行归并排序, 最后使两个排序好的部分合并

合并算法:

这里假设有2个各自有序的数列, 再制造一个空的数列

不断比较2个数列的头部, 哪个序列中的头部小(大), 就把那个值移动到空序列的尾部

如果一个数列已经为空, 那么直接复制另外一部分的序列的剩下部分到新数组的尾部

/*
 * left, middle, right 分别为左右下标值(非第几个值)
 */
void Merge(int A[], int left, int middle, int right) {

    // 1) left 小于或等于 middle
    // 2) i 初始值等于 left
    // 3) j 初始值等于 middle + 1
    int index = 0, i = left, j = middle + 1;
    int len = right - left + 1;
    int * B = new int[len];

    while (i <= middle && j <= right)
        B[index++] = A[i] < A[j] ? A[i++] : A[j++];
    // 4) i 不大于 middle
    while (i <= middle)
        B[index++] = A[i++];
    // 5) j 不大于 right
    while (j <= right)
        B[index++] = A[j++];

    i = left;
    while (i <= right)
        A[i++] = B[i - left];
}

/*
 * left, right 分别为左右下标值(非第几个值)
 */
void MergeSort(int A[], int left, int right) {
    if (left >= right) return;
    int middle = (left + right) / 2;
    MergeSort(A, left, middle);
    MergeSort(A, middle + 1, right);
    Merge(A, left, middle, right);
}

参考地址:

https://mp.weixin.qq.com/s/M51ikw9VmyJG5yTfDKQ5Ug

快速排序

解释:

1. 在一段数组中标记 left, right

2. 取 A[left] 作为第一个标准

3. 从 left + 1 开始往右, 吧筛选去大于 A[left] 的数

4. 从 right 开始往左, 筛选出小于 A[left] 的数

5. 不断地吧小于 A[left] 的数交换到左边, 吧大于 A[left] 的数换到右边

6. 吧 A[left] 的数替换到当中某个点 j (此时两边均符合条件且不一定有序)

7. 以 j 为中点, 分割数组, 并且递归快排

性能:

其性能取决于对称性, 越有序的, 效率越差

另外, 数组的顺序越短, 效率越差, 数组的数量小于 20 的时候, 建议改为冒泡排序

扩展问题:

1. 快速选择一个数组中第 k (小)大的数字

在快速排序第一部分结束后, 根据两个部分的数字个数, 判断数字在哪边

代码:

int Partition(int A[], int left, int right) {
    int i = left, j = right + 1;
    int x = A[left];
    while (1) {
        while (A[++i] < x && i < right);
        while (A[--j] > x);
        if (i >= j) break;
        Swap(A[i], A[j]);
    }
    A[left] = A[j];
    A[j] = x;
    return j;
}

void QuickSort(int A[], int left, int right) {
    if (left >= right) return;
    int q = Partition(A, left, right);
    QuickSort(A, left, q - 1);
    QuickSort(A, q + 1, right);
}

计数排序

解释:

如果是排在一定范围内的整数的话, 可以利用数字的大小值进行计算排序

1. 给定一段数组 A, 找到最大的数字(范围) max, 和长度

2. 生成一个空数组 B, 长度为最大的数字范围 max

3. 遍历数组 A, 将 A 的值都对应到 B上, 用 B 来记录哪个数字 (下标) 一共有多少个 (值)

4. 用 B 来重新生成 A

代码:

/*
 * 计数排序
 * 参数:
 *    A : 目标数组
 *  maxValue: 数组中的最大值
 *  len: 数组长度
 */
void CountingSort(int A[], int maxValue, int len) {
    // 新生成一个数组容器
    int * bucket = new int[maxValue + 1] { 0 };
    int sortedIndex = 0;

    for (int i = 0; i < len; i++) {
        // 将目标数组的每个数出现多少次都记录在 数组容器中
        bucket[A[i]]++;
    }
    // 利用数组容器的数据重新生成目标数组
    for (int i = 0; i <= maxValue; i++) {
        // 相同的数有多个
        // 则全都一次性生成到 A 数组中
        while (bucket[i]-- > 0) {
            A[sortedIndex++] = i;
        }
    }
}

参考地址:

https://mp.weixin.qq.com/s/Vq1dpZm2Mx_qeDofOuvObw

十大经典排序算法

https://www.cnblogs.com/onepixel/articles/7674659.html

外部排序:

指无法将数据一次性都加载到内存中进行排序

而要借助外存, 分批加载数据到内存进行排序, 最后整合的算法

对于外部排序的话, 最好是选择归并排序和快速排序这样分治类型的排序算法

其难点在于, 内存的容量总是小于外存的容量, 所以如何减少外存与内存之间数据的读写次为重点和难点

其中可以用来优化的策略是: 适当的进行多路归并(多路归并的规模不是越大越好)., 并且减少并行序列的数量(可以采用小顶堆的思路)

参考地址:

https://mp.weixin.qq.com/s/VJEddBB4FnWZESnnaNvz2g

posted @ 2018-05-15 11:08 `Laimic 阅读(276) 评论(0) 收藏举报

刷新页面返回顶部