面向对象设计与构造2022第三单元总结
一、分析在本单元自测过程中如何利用JML规格来准备测试数据
我在本单元的自测中主要采取了两种测试方法:普遍测试和专项测试。
所谓普遍测试就是数据生成器生成的数据包含作业指导书给出的所有指令,进行覆盖检查,但是每种指令的测试不一定是边界、极端情形。
而专项测试就是基于JML规格,针对那些过程复杂、容易写错和出现性能问题的指令生成特殊数据来测试。接下来举几个例子来说明。
首先是qgvs指令,从图论的角度来说其实就是维护一个群组里面人员所有边权和的两倍。我们来看JML是如何描述的
//in Network.java
/*@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id);
@ ensures \result == getGroup(id).getValueSum();
@ also
@ public exceptional_behavior
@ signals (GroupIdNotFoundException e) !(\exists int i; 0 <= i && i < groups.length;
@ groups[i].getId() == id);
@*/
public /*@ pure @*/ int queryGroupValueSum(int id) throws GroupIdNotFoundException;
//in Group.java
/*@ ensures \result == (\sum int i; 0 <= i && i < people.length;
@ (\sum int j; 0 <= j && j < people.length &&
@ people[i].isLinked(people[j]); people[i].queryValue(people[j])));
@*/
public /*@ pure @*/ int getValueSum();
所以直接从JML看,复杂度是\(O(指令数*组内人数^2)\)的
但其实从构造数据的角度我还需要关注的是
/*@ public normal_behavior
@ ...(省略)
@ also
@ public normal_behavior
@ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) &&
@ (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) &&
@ getGroup(id2).hasPerson(getPerson(id1)) == false &&
@ getGroup(id2).people.length >= 1111;
@ assignable \nothing;
@ also
@ public exceptional_behavior
@ ...(省略)
@*/
public void addToGroup(int id1, int id2) throws GroupIdNotFoundException,
PersonIdNotFoundException, EqualPersonIdException;
其实这个方法的JML就约束好了每个群组的人数不得超过1111个人。
因此可以构造人数达到上限的数据来检验时间复杂度是否合法,该部分的构造代码如下
#include <bits/stdc++.h>
using namespace std;
mt19937 rng(time(0));
int main()
{
freopen("testcase1.txt","w",stdout);
for(int i=1;i<=1111;i++)
{
printf("ap %d AAJ %d\n",i,rng()%200);
}
printf("ag 114514\n");
for(int i=1;i<=1111;i++)
{
printf("atg %d 114514\n",i);
}
for(int i=1;i<=2777;i++)
printf("qgvs 114514\n");
return 0;
}
然后,是qlc指令,我们来看一下它的JML。
/*@ public normal_behavior
@ requires contains(id);
@ ensures \result ==
@ (\min Person[] subgroup; subgroup.length % 2 == 0 &&
@ (\forall int i; 0 <= i && i < subgroup.length / 2; subgroup[i * 2].isLinked(subgroup[i * 2 + 1])) &&
@ (\forall int i; 0 <= i && i < people.length; isCircle(id, people[i].getId()) <==>
@ (\exists int j; 0 <= j && j < subgroup.length; subgroup[j].equals(people[i]))) &&
@ (\forall int i; 0 <= i && i < people.length; isCircle(id, people[i].getId()) <==>
@ (\exists Person[] connection;
@ (\forall int j; 0 <= j && j < connection.length - 1;
@ (\exists int k; 0 <= k && k < subgroup.length / 2; subgroup[k * 2].equals(connection[j]) &&
@ subgroup[k * 2 + 1].equals(connection[j + 1])));
@ connection[0].equals(getPerson(id)) && connection[connection.length - 1].equals(people[i])));
@ (\sum int i; 0 <= i && i < subgroup.length / 2; subgroup[i * 2].queryValue(subgroup[i * 2 + 1])));
@ also
@ public exceptional_behavior
@ signals (PersonIdNotFoundException e) !contains(id);
@*/
public /*@ pure @*/ int queryLeastConnection(int id) throws PersonIdNotFoundException;
正如老师在总结课上所言,其实这种最优化的描述是不太直观的,不过在阅读qlc的JML之前我们已经在测验环节中读过一个求边集的JML,所以有了经验。这里说白了就是要求id这个人所在连通块的最小生成树大小。
从构造数据角度,要检验最小生成树求解的效率和正确性,就是尽可能得让这个连通块的边数要多,而且权值要随机多样。构造代码如下
for(int i=1;i<=1111;i++)
{
printf("ap %d AAJ %d\n",i,rng()%200);
}
printf("ag 114514\n");
for(int i=1;i<=1111;i++)
{
printf("atg %d 114514\n",i);
}
for(int i=1;i<=1110;i++)
printf("ar %d %d %d\n",i,i+1,rng()%1000);
for(int i=1;i<=1109;i++)
printf("ar %d %d %d\n",i,i+2,rng()%1000);
for(int i=1;i<=538;i++)
printf("ar %d %d %d\n",rng()%1111+1,rng()%1111+1,rng()%1000);
for(int i=1;i<=20;i++)
printf("qlc %d\n",rng()%1111+1);
第三,是sim指令,JML太长就略去了。说白了就是除了发送信息外要求出从发送者到接收者的最短路。考虑到朴素的Dijkstra的复杂度是\(O(n^2)\),而堆优化的Dijkstra复杂度为\(O(m \log n)\),所以从构造数据角度,人数要达到\(10^3\)量级,同时信息数量与\(sim\)指令数一致达到上限,再加上边权随机性,就可以检测实现的正确性和效率了。
for i in range(0, 1111):
print("ap %d Jack%d %d" % (i, i, 20), file=file_out)
for i in range(0, 2889):
print(
"ar %d %d %d"
% (random.randint(0, 1111), random.randint(0, 1111), random.randint(0, 1000)),
file=file_out,
)
for i in range(0, 500):
print(
"am %d %d 0 %d %d"
% (
i,
random.randint(-1000, 1000),
random.randint(0, 1111),
random.randint(0, 1111),
),
file=file_out,
)
for i in range(0, 500):
print("sim %d" % (i), file=file_out)
第四,是dce指令。如果说前面的三种指令可能构造更多着眼于性能考虑,那么dce指令的测试就旨在检查正确性。
通过阅读JML,其实这条指令需要做两件事
-
将已经保存的表情中,热度小于\(limit\)的删掉
@ ensures (\forall int i; 0 <= i && i < \old(emojiIdList.length); @ (\old(emojiHeatList[i] >= limit) ==> @ (\exists int j; 0 <= j && j < emojiIdList.length; emojiIdList[j] == \old(emojiIdList[i])))); -
把所有信息里面,只保留非表情信息,和所含表情没有在第一步删掉的表情信息
@ ensures (\forall int i; 0 <= i && i < \old(messages.length); @ (\old(messages[i]) instanceof EmojiMessage && @ containsEmojiId(\old(((EmojiMessage)messages[i]).getEmojiId())) ==> @ (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i])))));
所以从构造数据来说,一方面人数要少,但是信息量要大,这样才能让每种表情的热度尽量高,另一方面可以让\(limit\)递减来进行dce.故构造代码如下
for i in range(0, 10):
print("ap %d Jack%d %d" % (i, i, 20), file=file_out)
for i in range(0, 10):
for j in range(1, 10 - i):
print("ar %d %d %d" % (i, i + j, random.randint(0, 1000)), file=file_out )
for i in range(0, 20):
print(
"sei %d" % (i),
file=file_out,
)
for i in range(0, 1000):
print(
"aem %d %d 0 %d %d"
% (i, random.randint(0, 19), random.randint(0, 9), random.randint(0, 9)),
file=file_out,
)
for i in range(0, 1000):
print("sm %d" % (i), file=file_out)
for i in range(0, 50):
print("dce %d" % (i), file=file_out)
for j in range(0, 20):
print("qp %d" % (j), file=file_out)
第五,是群发红包问题。这个地方我也差点写错了。关键处的JML就是这一句
@ ensures (\old(getMessage(id)) instanceof RedEnvelopeMessage) ==>
@ (\exists int i; i == ((RedEnvelopeMessage)\old(getMessage(id))).getMoney()/\old(getMessage(id)).getGroup().getSize();
@ \old(getMessage(id)).getPerson1().getMoney() ==
@ \old(getMessage(id).getPerson1().getMoney()) - i*(\old(getMessage(id)).getGroup().getSize() - 1) &&
@ (\forall Person p; \old(getMessage(id)).getGroup().hasPerson(p) && p != \old(getMessage(id)).getPerson1();
@ p.getMoney() == \old(p.getMoney()) + i));
- 发送的总钱数按照群组总人数均分,但是这个除法和Java运算符一致——是整除。所以会出现\(getMoney()\not=i*getSize()\)的情况
- 发送者扣钱但不扣“自己的那一份”,同样的,发钱也不发“自己的那一份”
但是在具体实现上,我是把这个\(i\)传到群组里,在群组里实现了一个方法,就是给所有人发钱\(i\)元。这就导致这条信息的发送者多得了一份钱。
这个问题是我在截止日那天上午才发现的,之所以大量的普遍测试没有触发这个bug,原因就是红包的钱数最多200,而普遍测试中往往给一个组塞了一千多号人,结果按照整除规则,其他人一分钱没得,发送者也根本没有发出去钱。
因此在专项测试中,人数一定要少,而且每发送一条消息,必须要检查发送者的钱数,再随机抽查两个人的钱数,这样就能较为充分地检查行为的正确性了。构造代码如下
for i in range(0, 10):
print("ap %d Jack%d %d" % (i, i, 20), file=file_out)
print("ag 114514", file=file_out)
for i in range(0, 10):
print("atg %d 114514" % (i), file=file_out)
send_people = []
for i in range(0,990):
sender = random.randint(0, 9)
send_people.append(sender)
print(
"arem %d %d 1 %d 114514" % (i, random.randint(0, 200), sender),
file=file_out,
)
for i in range(0, 990):
print("sm %d" % (i), file=file_out)
print("qm %d" % (send_people[i]), file=file_out)
for j in range(0, 2):
print("qm %d" % (random.randint(0, 9)), file=file_out)
二、梳理本单元的架构设计,分析自己的图模型构建和维护策略
首先还是放一张第三次作业时的UML图
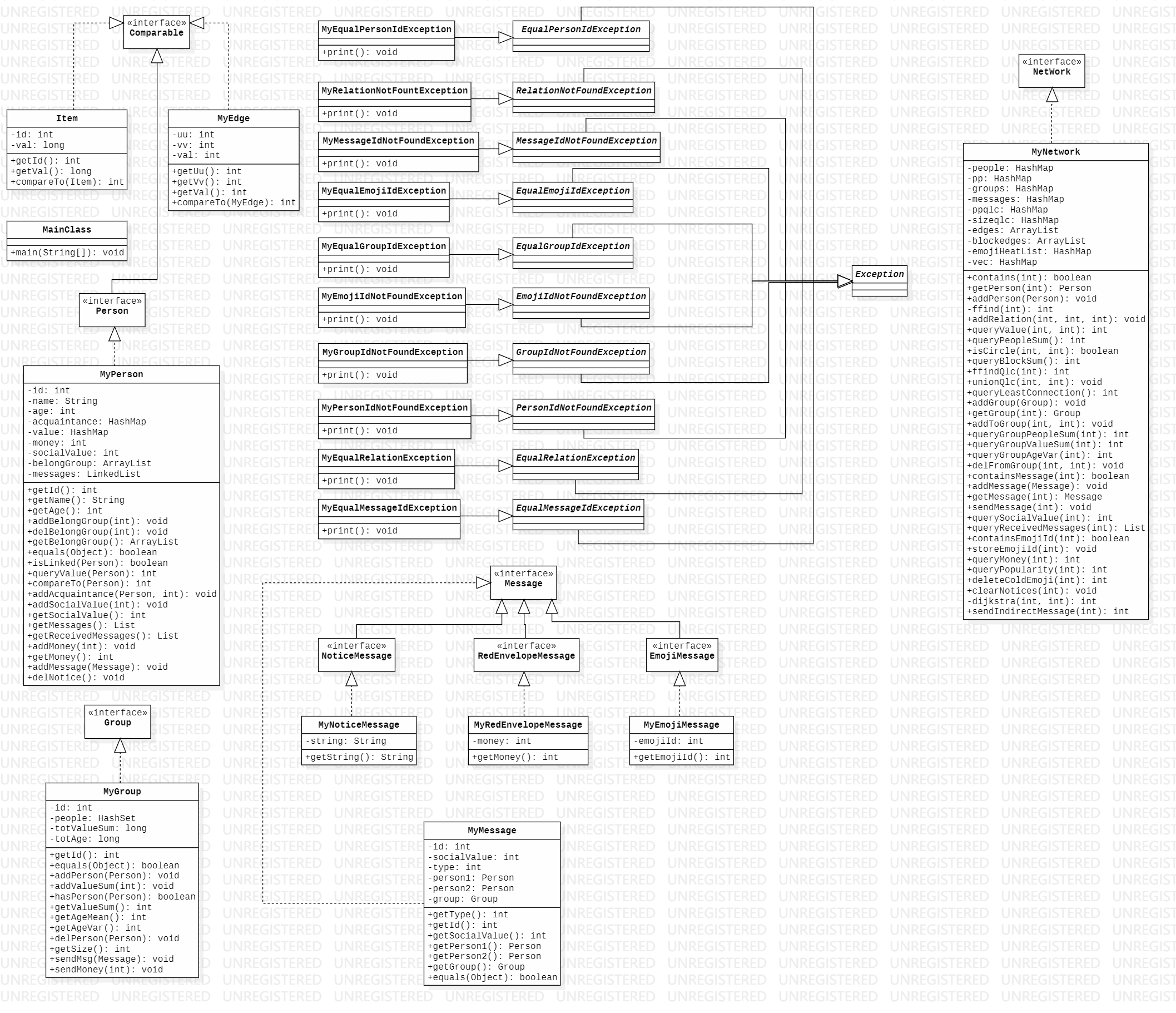
由图片可知,其实主体框架根据JML基本上已经确定了。自主实现的部分主要是图模型和一些辅助的方法上。
首先来说图模型,在求qci和qlc指令时维护了并查集,体现在UML图上就是MyNetwork里面的pp、ppqlc和sizeqlc三个HashMap,和ffind、ffindQlc和unionQlc三个方法。其中pp和ffind主要是用并查集维护图的连通性,便于qci指令中回答两个人是否连通。而ppqlc、sizeqlc和剩下两个方法,其实是在用Kruskal算法求最小生成树中维护并查集的。为了避免混淆,所以单独又实现了一下。当然,用于qci的并查集简单采用路径压缩,而在Kruskal算法中的并查集是路径压缩+按秩合并的,以尽可能提高效率。
为了方便Kruskal算法,新建了一个MyEdge类,可以存储一条边的两个节点和边权,并实现了Comparable接口,使得其可以排序.
那么到了sim指令需要写堆优化的Dijkstra算法时,需要维护一个无向图,邻接表的出现就很有必要了。于是在MyNetwork中有了一个private HashMap<Integer, HashMap<Integer, Integer>> vec;来存起点、终点和这条边的权值(本单元根据JML规格不会出现重边,所以这么维护倒也无妨)。那么在实现Dijkstra中,使用优先队列PriorityQueue来选取当前起点所到达的各个点中路径长度最小的一个点,这里也新建了一个Item类来方便PriorityQueue的操作。
还有一处图模型,就是qgvs需要知道一个群组里所有连边的权值和*2.不过这里仅仅需要一个数值,并不需要实际维护里面的图结构。需要注意的就是在人员刚刚加入群组的时候,对群组权值和贡献,人员退出的时候,减去贡献。特殊的情形就是两个人可能之前已经属于一个(或多个)群组,但还没有建立关系,这个时候addRelation需要考虑到对所有共同加入的群组进行贡献。
三、按照作业分析代码实现出现的性能问题和修复情况
由于在设计阶段充分考虑了各种指令的最坏时间复杂度,并且在自测阶段测试较为充分,故最终提交的作业里没有出现性能问题。
四、请针对下页ppt内容对Network进行扩展,并给出相应的JML规格
假设出现了几种不同的Person
- Advertiser:持续向外发送产品广告
- Producer:产品生产商,通过Advertiser来销售产品
- Customer:消费者,会关注广告并选择和自己偏好匹配的产品来购买 -- 所谓购买,就是直接通过Advertiser给相应Producer发一个购买消息
- Person:吃瓜群众,不发广告,不买东西,不卖东西
如此Network可以支持市场营销,并能查询某种商品的销售额和销售路径等 请讨论如何对Network扩展,给出相关接口方法,并选择3个核心业务功能的接口方法撰写JML规格(借鉴所总结的JML规格模式)
首先,针对广告和订购两种消息新建接口
广告消息:继承自Message接口,且要求type=2,(仅初始化Person1)JML如下
public interface AdMessage extends Message{
/*@
@ public instance model int productId;
@ public instance model int price;
@*/
//@ public invariant socialValue == price;
//@ ensures \result == productId;
public /*@ pure @*/ int getProductId();
//@ ensures \result == price;
public /*@ pure @*/ int getPrice();
}
订购消息:继承自Message接口,且要求type=3(初始化Person1和Person2),JML如下
public interface PurchaseMessage extends Message{
/*@
@ public instance model int productId;
@ public instance model int quantity;
@ public instance model int producerId;
@*/
//public invariant socialValue == quantity;
//@ ensures \result == productId;
public /*@ pure @*/ int getProductId();
//@ ensures \result == quantity;
public /*@ pure @*/ int getQuantity();
//@ ensures \result == producerId;
public /*@ pure @*/ int getProducerId();
}
然后考虑除Person以外的三类人员,新建接口
public interface Advertiser extends Person{
/*@
@ public instance model Producer[] producers; //所经销的生产厂家
@ public instance model int[] products;//所经销的产品号
@*/
// ensures \result == (\exists int i; 0 <= i && i < producers.length(); producers[i].getId() == id);
public /*@ pure @*/ boolean containsProducer(int id);
// ensures \result == (\exists int i; 0 <= i && i< products.length(); products[i] == id);
public /*@ pure @*/ boolean containsProduct(int id);
}
public interface Producer extends Person{
/*@
@ public instance model Advertiser[] advertisers; //经销商
@ public instance model int[] products;//所生产的产品号
@*/
// ensures \result == (\exists int i; 0 <=i && i < advertisers.length(); advertisers[i].getId() == id);
public /*@ pure @*/ boolean containsAdvertiser(int id);
// ensures \result == (\exists int i; 0 <= u && i< products.length(); products[i] == id);
public /*@ pure @*/ boolean containsProduct(int id);
}
putlic interface Customer extends Person{
}
然后在Network中新增四个方法
- 发送广告:考虑Advertiser也属于普通用户(继承自Person),而并非微店,所以实际微信中更类似于“朋友圈营销”的广告方式,因此这里限定TA只能向有好友(isLinked)的Customer和吃瓜群众发送广告。
- 发送订单
- 查询某种商品的销售额
- 查询某种商品的销售路径:输出为一个四元组的列表,每一个四元组为
(生产者、经销商、消费者、数量)
//四元组,这里就不用JML了
public class Item{
private Person producer;
private Person advertiser;
private Person customer;
private int quantity;
private int productId;
public Item(Person producer, Person advertiser, Person customer, int quantity, int productId)
{
this.producer = producer;
this.advertiser = advertiser;
this.customer = customer;
this.quantity = quantity;
hits.productId = productId;
}
public int getId()
{
return productId;
}
}
方法的JML
public interface Network
{
//省略已有的public instance model
/*@ public instance model non_null Item[] paths;
public instance model non_null int[] productSoldout;
@*/
//省略已有的方法
/*@ public normal_behavior
@ requires containsMessage(id) && (getMessage(id) instanceof AdMessage)&&(getMessage(id).getType==2) && (getMessage(id).getPerson1() instanceof Advertiser)
@ assignable getMessage(id).getPerson1().socialValue
@ assignable people[*].socialValue, people[*].messages
@ ensures \old(getMessage(id)).getPerson1().getSocialValue() ==
@ \old(getMessage(id).getPerson1().getSocialValue()) + \old(getMessage(id)).getSocialValue()
@ ensures (\forall int i; 0 <= i && i < \old(people).length() && \old(people[i]).isLinked(getMessage(id).getPerson1()) && !(\old(people[i]) instanceof Advertiser) && !(\old(people[i]) instanceof Producer); \old(people[i]).getSocialValue() == \old(people[i].getSocialValue()) + \old(getMessage(id)).getSocialValue();
@ ensures (\forall int i; 0 <=i && i < \old(people).length() && \old(people[i]).isLinked(getMessage(id).getPerson1()) && !(\old(people[i]) instanceof Advertiser) && !(\old(people[i]) instanceof Producer);
(\forall int j; 0 <= j && j < \old(people[i].getMessages().size()); \old(people[i]).getMessages().get(i+1) = \old(people[i].getMessages().get(i))));
@ ensures (\forall int i; 0 <=i && i < \old(people).length() && \old(people[i]).isLinked(getMessage(id).getPerson1()) && !(\old(people[i]) instanceof Advertiser) && !(\old(people[i]) instanceof Producer); \old(people[i]).getMessages().get(0).equals(\old(getMessage(id)));
@ also
@ public exceptional_behavior
@ signals (MessageIdNotFoundException e) !containsMessage(id);
@ signals (InvalidMessageTypeException e) containsMessage(id) && (!(getMessage(id) instanceof AdMessage) || ((getMessage(id) instanceof AdMessage) && getMessage(id).getType!=2));
@ signals (InvalidPersonTypeException e) containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==2) && !(getMessage(id).getPerson1() instanceof Advertiser)
@*/
public void sendAdMessage(int id) throws MessageIdNotFoundException, InvalidMessageTypeException, InvalidPersonTypeException;
/*@ public normal_behavior
@ requires containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==3) && ((getMessage(id).getPerson1() instanceof Customer) && (getMessage(id).getPerson2() instanceof Advertiser) && (getPerson(getMessage(id).getProducerId()) instanceof Producer)) && (((Advertiser)getMessage(id).getPerson2()).containsProduct(getMessage(id).getProductId()));
@ assignable getMessage(id).getPerson2().messages, paths, productSoldout;
@ ensures (\forall int i; 0 <= i && i < \old(getMessage(id).getPerson2()).getMessages().size());
\old(getMessage(id).getPerson2()).getMessages().get(i+1) = \old(getMessage(id).getPerson2().getMessages().get(i));
@ ensures \old(getMessage(id).getPerson2()).getMessages().get(0).equals(getMessage(id));
@ ensures \old(getMessage(id).getPerson2()).getMessages().size() == \old(getMessage(id).getPerson2().getMessages().size()) + 1;
@ ensures productSoldout[((PurchaseMessage)getMessage(id)).getProductId()] == \old(productSoldout[((PurchaseMessage)getMessage(id)).getProductId()]) + ((PurchaseMessage)getMessage(id)).getQuantity();
@ ensures (\exist int i; 0 <= i && i < paths.length(); paths[i].equals(new Item(getPerson(((PurchaseMessage)getMessage(id)).getProducerId(), getMessage().getPerson2(), getMessage().getPerson1(), ((PurchaseMessage)getMessage(id)).getQuantity(), ((PurchaseMessage)getMessage(id)).getProductId());
@ also
@ public exceptional_behavior
@ signals (MessageIdNotFoundException e) !containsMessage(id);
@ signals (InvalidMessageTypeException e) containsMessage(id) && (!(getMessage(id) instanceof PurchaseMessage) || ((getMessage(id) instanceof PurchaseMessage) && getMessage(id).getType!=2));
@ signals (InvalidPersonTypeException e) containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==3) && (!(getMessage(id).getPerson1() instanceof Customer) || !(getMessage(id).getPerson2() instanceof Advertiser) || (!getPerson(getMessage(id).getProducerId()) instanceof Producer));
@ signals (ProductIdNotFoundException e) containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==3) && ((getMessage(id).getPerson1() instanceof Customer) && (getMessage(id).getPerson2() instanceof Advertiser) && (getPerson(getMessage(id).getProducerId()) instanceof Producer)) && !(((Advertiser)getMessage(id).getPerson2()).containsProduct(getMessage(id).getProductId()));
@*/
public void sendPurchaseMessage(int id) throws MessageIdNotFoundException, InvalidMessageTypeException, InvalidPersonTypeException, ProductIdNotFoundException;
/*@ public normal_behavior
@ ensures \result == productSoldout[id];
@*/
public /*@ pure @*/ int getSaledata(int id);
/*@ public normal_behavior
@ ensures (\forall int i; 0 <=i && i < paths.length() && paths[i].getId() == id;
\result.contains(paths[i]));
@*/
public List<Item> getSalePath(int id);
}
五、本单元学习体会
这个单元相比于前两个单元的设计和编码工作量确实小了不少,不过初次接触JML规格的时候,会有一种“带着镣铐跳舞”的感觉——首先JML给出的各种约束和限制是必须要满足的,在满足的基础上,还要去思考如何提高效率,比如选择怎么样的容器,选择怎么样的算法。
最为重要的是,这个单元的测试与前面两个单元的很大不同在于所谓的“题目数据限制”可谓是“无处不在”,因为任何一处JML语句都不能忽视。一方面可以用Junit工具来显式地验证一些前置后置条件的满足情况,另一方面对于编写数据生成器进行大量测试而言,能不能击中缺陷其实是很大的问题。典型的例子就是上面提到了,即便做了大量的普遍测试(比如上万组),但是因为普遍数据生成器构造的不足,触发不了bug,那么某种程度上自测就白测了。
因此,我觉得黑盒白盒测试(包括代码通读)都要认真做,不可偏废。尤其是现在还没有自动根据JML生成Junit测试的情况下,即便是编写数据生成器,也还是基于人工对JML的语义理解,如果对JML语义理解有偏差,那么就谈不上测试的有效性。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号