思维题练习专场-DP篇(附题表)
转载请注明原文地址http://www.cnblogs.com/LadyLex/p/8536399.html
听说今年省选很可怕?刷题刷题刷题
省选已经结束了但是我们要继续刷题刷题刷题
目标是“有思维难度的DP题”!
一,uoj316
这个不用多说……NOI2017的D1T3,难度肯定是有的
个人觉得那个dp方程难想……

1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 using namespace std; 5 #define mod 998244353 6 #define K 1010 7 #define L 2048 8 #define RG register 9 #define LL long long 10 inline int quick_mod(int di,int mi) 11 { 12 int ret=1; 13 for(;mi;mi>>=1,di=(LL)di*di%mod) 14 if(mi&1)ret=(LL)ret*di%mod; 15 return ret; 16 } 17 int poww[L],logi[L],rev[L],len=1; 18 inline void dft(int *a,int ra,int opt) 19 { 20 register int i,j,l,d=logi[len]-logi[ra],wn,tmp,*w,*x,*y; 21 for(i=0;i<ra;++i)if(i<(rev[i]>>d))swap(a[i],a[rev[i]>>d]); 22 for(d=2;d<=ra;d<<=1) 23 for(wn=((opt==1)?(len/d):(-len/d)),i=0,l=(d>>1);i<ra;i+=d) 24 for(w=poww+(opt==1?0:len),j=0,x=a+i,y=x+l;j<l;++j,++x,++y,w+=wn) 25 tmp=(LL)(*w)*(*y)%mod,*y=(*x-tmp+mod)%mod,*x=(*x+tmp)%mod; 26 if(opt==-1) 27 for(tmp=quick_mod(ra,mod-2),i=0;i<ra;++i)a[i]=(LL)a[i]*tmp%mod; 28 } 29 int n,k,p,q,pp[K]; 30 int g[K][K],h[K][K],f[K<<1]; 31 inline int min(int a,int b){return a<b?a:b;} 32 int tmp1[L]; 33 inline int get_inv(int *a,int *ret,int ra) 34 { 35 if(ra==1){ret[0]=quick_mod(a[0],mod-2);return 1;} 36 RG int i,la=1,r1=get_inv(a,ret,ra+1>>1); 37 while(la<(ra<<1))la<<=1; 38 memcpy(tmp1,a,ra<<2),memset(tmp1,0,(la-ra)<<2); 39 memset(ret,0,(la-r1)<<2); 40 dft(tmp1,la,1),dft(ret,la,1); 41 for(i=0;i<la;++i)ret[i]=(LL)ret[i]*(2+mod-(LL)tmp1[i]*ret[i]%mod)%mod; 42 dft(ret,la,-1);return ra; 43 } 44 inline void rev_copy(int *to,int *st,int ra) 45 {for(RG int i=0;i<ra;++i,++to)*to=st[ra-i-1];} 46 inline void reverse(int *st,int ra) 47 {for(RG int t,i=0,j=ra-1;i<j;++i,--j)t=st[i],st[i]=st[j],st[j]=t;} 48 int tmp2[L],tmp3[L]; 49 inline int get_mod(int *a,int ra,int *p,int rp,int *ret) 50 { 51 while(ra&&!a[ra-1])--ra; 52 while(rp&&!p[rp-1])--rp; 53 if(ra<rp){memcpy(ret,a,ra<<2),memset(ret+ra,0,(rp-ra)<<2);return rp;} 54 RG int i,j,re=ra-rp+1,la=1; 55 while(la<(re<<1))la<<=1; 56 rev_copy(tmp2,p,rp);memset(tmp2+re,0,(la-re)<<2); 57 get_inv(tmp2,tmp3,re),memset(tmp3+re,0,(la-re)<<2); 58 rev_copy(tmp2,a,ra),memset(tmp2+re,0,(la-re)<<2); 59 dft(tmp3,la,1);dft(tmp2,la,1); 60 for(i=0;i<la;++i)tmp2[i]=(LL)tmp2[i]*tmp3[i]%mod; 61 dft(tmp2,la,-1); 62 la=1;while(la<ra)la<<=1; 63 reverse(tmp2,re), 64 memset(tmp2+re,0,(la-re)<<2); 65 memcpy(tmp3,p,rp<<2),memset(tmp3+rp,0,(la-rp)<<2); 66 dft(tmp2,la,1),dft(tmp3,la,1); 67 for(i=0;i<la;++i)tmp2[i]=(LL)tmp2[i]*tmp3[i]%mod; 68 dft(tmp2,la,-1); 69 for(i=0;i<rp;++i)ret[i]=(a[i]-tmp2[i]+mod)%mod; 70 memset(ret+rp,0,(la-rp)<<2); 71 while(rp&&!ret[rp-1])--rp; 72 return rp; 73 } 74 int c[L],d[L],e[L],tmp[L]; 75 inline int calc(int k) 76 { 77 RG int i,j,u,ra=k+1,r1=k+2,lim,la=1; 78 memset(g,0,sizeof(g)); 79 memset(h,0,sizeof(h)); 80 g[k][1]=(LL)pp[k]*q%mod; 81 g[k][0]=h[k][0]=1; 82 for(i=k-1;i>0;--i) 83 { 84 ra=k/i,g[i][0]=h[i][0]=1; 85 for(j=1;j<=ra;++j) 86 for(u=0;u<j;++u) 87 h[i][j]=(h[i][j]+(LL)h[i][u]*g[i+1][j-u-1]%mod*pp[i]%mod*q)%mod; 88 for(j=1;j<=ra;++j) 89 for(u=0;u<=j;++u) 90 g[i][j]=(g[i][j]+(LL)h[i][u]*g[i+1][j-u])%mod; 91 } 92 memset(f,0,sizeof(f)),f[0]=1; 93 for(i=1;i<=(ra<<1);++i) 94 for(j=1,lim=min(k+1,i);j<=lim;++j) 95 f[i]=(f[i]+(LL)f[i-j]*g[1][j-1]%mod*q)%mod; 96 int ret=0; 97 if(n<=(ra<<1)) 98 { 99 for(i=max(0,n-k);i<=n;++i) 100 ret=(ret+(LL)f[i]*g[1][n-i])%mod; 101 return ret; 102 } 103 memset(c,0,sizeof(c)),c[1]=1; 104 memset(d,0,sizeof(d));d[ra]=1; 105 for(i=1;i<=ra;++i)d[ra-i]=(LL)q*g[1][i-1]%mod; 106 memset(e,0,sizeof(e)),e[0]=1; 107 while(la<(ra<<1))la<<=1; 108 for(lim=n-k-1;lim;lim>>=1) 109 { 110 if(lim&1) 111 { 112 memcpy(tmp,c,k<<2);memset(tmp+k,0,(la-k)<<2); 113 dft(e,la,1),dft(tmp,la,1); 114 for(i=0;i<la;++i)e[i]=(LL)e[i]*tmp[i]%mod; 115 dft(e,la,-1); 116 get_mod(e,k<<1,d,ra,e); 117 } 118 dft(c,la,1); 119 for(i=0;i<la;++i)c[i]=(LL)c[i]*c[i]%mod; 120 dft(c,la,-1); 121 get_mod(c,k<<1,d,ra,c); 122 } 123 124 } 125 int main() 126 { 127 RG int i,x,y; 128 scanf("%d%d%d%d",&n,&k,&x,&y);logi[1]=0; 129 while(len<=(k+1<<1))len<<=1,logi[len]=logi[len>>1]+1; 130 poww[0]=poww[len]=1,poww[1]=quick_mod(3,(mod-1)/len); 131 for(i=2;i<len;++i)poww[i]=(LL)poww[i-1]*poww[1]%mod; 132 for(i=0;i<len;++i) 133 if(i&1)rev[i]=(rev[i>>1]>>1)|(len>>1); 134 else rev[i]=(rev[i>>1]>>1); 135 p=(LL)x*quick_mod(y,mod-2)%mod,q=(LL)(y-x)*quick_mod(y,mod-2)%mod; 136 for(pp[0]=1,pp[1]=p,i=2;i<=k;++i)pp[i]=(LL)pp[i-1]*p%mod; 137 printf("%d\n",(calc(k)-calc(k-1)+mod)%mod); 138 }
二,bzoj3326
题目模型不算特别新的数位DP,能想到它在干什么,但是……
那个式子,想推对必须非常严谨才行……

1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 #define RG register 5 #define mod 20130427 6 #define N 100010 7 #define LL long long 8 char cB[1<<15],*S=cB,*T=cB; 9 #define getc (S==T&&(T=(S=cB)+fread(cB,1,1<<15,stdin),S==T)?0:*S++) 10 inline int read() 11 { 12 RG int x=0;RG char c=getc; 13 while(c<'0'|c>'9')c=getc; 14 while(c>='0'&c<='9')x=10*x+(c^48),c=getc; 15 return x; 16 } 17 inline int Sum(int a){return ((LL)a*(a+1ll)/2)%mod;} 18 inline int max(int a,int b){return a>b?a:b;} 19 inline int min(int a,int b){return a<b?a:b;} 20 int ge2[N],sum2[N],ge3[N],sum3[N],no_zero_sum3[N],B,lena,bit[N],lenb,bin[N]; 21 inline int calc(bool start,int left,int lim,int cnt,int sum,int sum_of_substring ) 22 { 23 if(lim==0)return 0; 24 if(start) 25 return 26 ( 27 (LL) Sum(lim-1) * ge2[left] %mod * bin[left] %mod + //前与后连接之后前面的贡献 28 (LL) ( lim - 1 ) %mod * sum3[left] %mod + no_zero_sum3[left] %mod +//后面的子串 29 (LL) ( lim - 1 ) %mod * sum2[left] %mod//前与后连接之后后面的贡献 30 )%mod; 31 int new_sum=( (LL) sum * B %mod * lim %mod + (LL) Sum(lim-1) * cnt %mod ) %mod; 32 return 33 ( 34 (LL) sum_of_substring * lim %mod * bin[left] %mod + //之前的子串 35 (LL) new_sum * ge2[left] %mod * bin[left] %mod + //前与后连接之后前面的贡献 36 (LL) lim %mod * sum3[left] %mod +//后面的子串 不乘cnt 37 (LL) cnt * lim %mod * sum2[left] %mod//前与后连接之后后面的贡献 ,要乘cnt 因为再前面不同 38 )%mod; 39 } 40 inline int dfs(bool start,int st,int cnt,int sum,int sum_of_substring) 41 { 42 if(st==0)return 0; 43 int new_sum=( (LL) sum * B %mod + (LL) ( cnt + 1 ) * bit[st] %mod )%mod; 44 return 45 ( new_sum + calc(start, st-1 , bit[st] , cnt + 1 , sum , sum_of_substring ) + 46 dfs(0, st - 1 , cnt + 1, new_sum , (sum_of_substring + new_sum)%mod ) )%mod; 47 } 48 signed main() 49 { 50 RG int i,j,len,ans; 51 B=read(),lena=read(); 52 for(i=lena;i;--i)bit[i]=read(); 53 lenb=read();len=max(lena,lenb); 54 if(lena>1||bit[1]>0) 55 { 56 --bit[1],j=1; 57 while(bit[j]<0)bit[j]+=B,--bit[j+1],++j; 58 while(lena>1&&!bit[lena])--lena; 59 } 60 for(bin[0]=ge2[0]=i=1;i<=len;++i) 61 { 62 bin[i]=(LL)bin[i-1]*B%mod; 63 ge2[i]=( ge2[i-1] + bin[i] )%mod; 64 ge3[i]=(LL) Sum(i) * bin[i] %mod; 65 sum2[i]=( (LL) sum2[i-1] * B %mod + Sum ( bin[i] - 1 ) )%mod; 66 sum3[i]=( (LL) Sum(B-1) * bin[i-1] %mod * ge2[i-1] %mod + (LL)B * sum2[i-1] %mod + (LL) B * sum3[i-1] %mod )%mod; 67 no_zero_sum3[i]=( (LL) Sum(B-1) * bin[i-1] %mod * ge2[i-1] %mod + 68 (LL) (B - 1) * sum2[i-1] %mod + (LL) (B - 1) * sum3[i-1] %mod + no_zero_sum3[i-1] )%mod; 69 } 70 ans=mod-dfs(1,lena,0,0,0); 71 for(i=lenb;i;--i)bit[i]=read(); 72 printf("%d\n",(ans+dfs(1,lenb,0,0,0))%mod); 73 }
三,bzoj4513
二进制的数位DP
听dalao们说挺简单……但是我觉得是比较好的一道数位dp
wq的做法又简洁又快,但是我太弱了不会……
只好打一个稍微麻烦的dp了

1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 using namespace std; 5 #define RG register 6 #define LL long long 7 LL n,m,k,bin[64],f_ge[64][2][2][2],f_sum[64][2][2][2]; 8 int main() 9 { 10 RG int mod,i,j,ta,tb,tc,a,b,c,x,y,z,t,len,lena,lenb,lenc,bita,bitb,bitc;LL ans,tmp; 11 scanf("%d",&t); 12 while(t--) 13 { 14 scanf("%lld%lld%lld%d",&n,&m,&k,&mod),--n,--m; 15 lena=lenb=lenc=0; 16 tmp=n;while(tmp)++lena,tmp>>=1; 17 tmp=m;while(tmp)++lenb,tmp>>=1; 18 tmp=k;while(tmp)++lenc,tmp>>=1; 19 len=max(lena,max(lenb,lenc)); 20 for(bin[0]=i=1;i<=len;++i)bin[i]=(bin[i-1]<<1)%mod; 21 memset(f_ge,0,sizeof(f_ge)),memset(f_sum,0,sizeof(f_sum)); 22 f_ge[len+1][1][1][1]=1;ans=0; 23 for(i=len;~i;--i) 24 { 25 bita=(n>>i)&1,bitb=(m>>i)&1,bitc=(k>>i)&1; 26 for(a=0;a<2;++a)for(b=0;b<2;++b)for(c=0;c<2;++c) 27 if(f_ge[i+1][a][b][c]) 28 for(x=0;x<2;++x) 29 { 30 if(a && x>bita)break; 31 for(y=0;y<2;++y) 32 { 33 if(b && y>bitb)break; 34 z=x^y; 35 if(c && z<bitc)continue; 36 ta=(a && bita==x)?1:0,tb=(b && bitb==y)?1:0,tc=(c && bitc==z)?1:0; 37 f_ge[i][ta][tb][tc]=(f_ge[i][ta][tb][tc]+f_ge[i+1][a][b][c])%mod; 38 f_sum[i][ta][tb][tc]=( f_sum[i][ta][tb][tc]+f_sum[i+1][a][b][c])%mod; 39 if(z)f_sum[i][ta][tb][tc]=( f_sum[i][ta][tb][tc]+ bin[i]*f_ge[i+1][a][b][c]%mod )%mod; 40 } 41 } 42 } 43 k%=mod; 44 for(a=0;a<2;++a)for(b=0;b<2;++b)for(c=0;c<2;++c) 45 ans=(ans+f_sum[0][a][b][c]-k*f_ge[0][a][b][c]%mod+mod)%mod; 46 printf("%lld\n",ans); 47 } 48 }
四,uoj141
很棒的插头(轮廓线)dp题目……我从一开始就没有想出来……

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define LL long long 6 #define RG register 7 #define N 15 8 #define mod 998244353 9 #define D 51 10 #define SZ 612497 11 int n,m,ans[110]; 12 LL K,B[N][N],lower,bin[15]; 13 char row[N],line[N]; 14 struct node{LL state;int next,cnt,val;}; 15 struct hash_map 16 { 17 node s[SZ+10];int e,adj[SZ+10]; 18 inline void init(){e=0;memset(adj,0,sizeof(adj));} 19 inline void update(LL state,int val,int cnt) 20 { 21 RG int i,pos=(state%SZ+(LL)val*SZ)%SZ; 22 for(i=adj[pos];i&&(s[i].state!=state||s[i].val!=val);i=s[i].next); 23 if(!i)s[++e].state=state,s[e].val=val,s[e].cnt=cnt,s[e].next=adj[pos],adj[pos]=e; 24 else s[i].cnt=(s[i].cnt+cnt)%mod; 25 } 26 }f[2]; 27 inline void execute(int x,int y,int cur) 28 { 29 RG int i,j,last=cur^1,tot=f[last].e,val,val1,val2,cnt,sum,half; 30 LL state,nstate; 31 f[cur].init(); 32 for(i=1;i<=tot;++i) 33 { 34 state=f[last].s[i].state,val=f[last].s[i].val,cnt=f[last].s[i].cnt; 35 nstate=state%bin[y-1],state/=bin[y-1]; 36 val1=state%D,state/=D; 37 val2=state%D,state/=D; 38 sum=val1+val2+B[x][y],half=sum>>1; 39 f[cur].update(nstate+state*bin[y+1]+(sum-half)*bin[y]+half*bin[y-1],val,cnt); 40 f[cur].update(nstate+state*bin[y+1]+half*bin[y]+(sum-half)*bin[y-1],val,cnt); 41 } 42 } 43 int main() 44 { 45 RG int i,j,cur=0; 46 for(bin[0]=i=1;i<=11;++i)bin[i]=bin[i-1]*D; 47 scanf("%d%d%lld",&n,&m,&K); 48 scanf("%s",row+1),scanf("%s",line+1); 49 B[1][1]=K; 50 for(i=1;i<=n;++i) 51 for(j=1;j<=m;++j) 52 B[i+1][j]+=B[i][j]>>1,B[i][j+1]+=B[i][j]>>1,B[i][j]&=1; 53 for(i=1;i<=n;++i)if(row[i]=='1')lower+=B[i][m+1]; 54 for(j=1;j<=m;++j)if(line[j]=='1')lower+=B[n+1][j]; 55 f[0].update(0,0,1); 56 RG int tot,last,val,cnt;LL state; 57 for(i=1;i<=n;++i) 58 { 59 for(j=1;j<=m;++j)cur^=1,execute(i,j,cur); 60 cur^=1,last=cur^1;tot=f[last].e; 61 f[cur].init(); 62 for(j=1;j<=tot;++j) 63 { 64 state=f[last].s[j].state,val=f[last].s[j].val; 65 if(row[i]=='1')val+=state/bin[m]; 66 state=(state%bin[m])*D; 67 f[cur].update(state,val,f[last].s[j].cnt); 68 } 69 } 70 for(i=1;i<=f[cur].e;++i) 71 { 72 state=f[cur].s[i].state/D; 73 val=f[cur].s[i].val; 74 for(j=1;j<=m;++j,state/=D)if(line[j]=='1')val+=state%D; 75 ans[val]=(ans[val]+f[cur].s[i].cnt)%mod; 76 } 77 for(i=1;i<=n*m;++i)ans[i]=(ans[i]+ans[i-1])%mod; 78 RG int q;LL l,r; 79 scanf("%d",&q); 80 while(q--) 81 { 82 scanf("%lld%lld",&l,&r); 83 if(r<lower||l>lower+n*m){puts("0");continue;} 84 l=max(0ll,l-lower),r=min((LL)n*m,r-lower); 85 printf("%d\n",l?(ans[r]-ans[l-1]+mod)%mod:ans[r]); 86 } 87 }
五,uoj129
NOI2015D1T3,难度还是稍微有的
我自己只想出了50pts做法,其实只差一点,把n/2改成$\sqrt(n)$的复杂度就行了

1 #include <cstdio> 2 #include <cstring> 3 #include <vector> 4 using namespace std; 5 inline int min(int a,int b){return a<b?a:b;} 6 #define RG register 7 #define LL long long 8 #define N 510 9 #define L 266 10 int f[L][L],g[2][L][L]; 11 vector<int>cont[N]; 12 int n,mod,ans,lim,full,prime[N],id[N],tot;bool vis[N]; 13 int bin[10]; 14 inline void print(int s) 15 { 16 for(RG int i=0;i<lim;++i)printf("%d",(s>>i)&1 ); 17 printf("\n"); 18 } 19 signed main() 20 { 21 scanf("%d%d",&n,&mod); 22 RG int x,y,z,tmp,i,j,k; 23 for(i=2;i<=n;++i) 24 { 25 if(!vis[i])prime[++tot]=i,id[i]=tot; 26 for(j=1;(x=i*prime[j])<=n;++j) 27 {vis[x]=1;if(i%prime[j]==0)break;} 28 } 29 lim=min(8,tot),full=(1<<lim)-1; 30 for(bin[0]=i=1;i<=lim;++i)bin[i]=bin[i-1]<<1; 31 for(i=2;i<=n;++i) 32 { 33 for(x=i,y=0,j=1;j<=lim;++j) 34 if(x%prime[j]==0) 35 { 36 y|=bin[j-1]; 37 while(x%prime[j]==0)x/=prime[j]; 38 } 39 cont[id[x]].push_back(y); 40 } 41 f[0][0]=1; 42 for(x=0,y=cont[0].size();x<y;++x) 43 { 44 memcpy(g[0],f,sizeof(f)); 45 memcpy(g[1],f,sizeof(f)); 46 for(i=full;~i;--i) 47 for(j=full;~j;--j) 48 if((i&j)==0) 49 { 50 if((cont[0][x]&j)==0)g[0][i|cont[0][x]][j]=(g[0][i|cont[0][x]][j]+g[0][i][j])%mod; 51 if((cont[0][x]&i)==0)g[1][i][j|cont[0][x]]=(g[1][i][j|cont[0][x]]+g[1][i][j])%mod; 52 } 53 for(i=full;~i;--i) 54 for(j=full;~j;--j) 55 if((i&j)==0)f[i][j]=(g[0][i][j]+g[1][i][j]-f[i][j])%mod; 56 } 57 for(k=1;k<=tot;++k) 58 { 59 memcpy(g[0],f,sizeof(f)); 60 memcpy(g[1],f,sizeof(f)); 61 for(x=0,y=cont[k].size();x<y;++x) 62 { 63 for(i=full;~i;--i) 64 for(j=full;~j;--j) 65 if((i&j)==0) 66 { 67 if((cont[k][x]&j)==0)g[0][i|cont[k][x]][j]=(g[0][i|cont[k][x]][j]+g[0][i][j])%mod; 68 if((cont[k][x]&i)==0)g[1][i][j|cont[k][x]]=(g[1][i][j|cont[k][x]]+g[1][i][j])%mod; 69 } 70 } 71 for(i=full;~i;--i) 72 for(j=full;~j;--j) 73 if((i&j)==0)f[i][j]=((LL)g[0][i][j]+g[1][i][j]-f[i][j])%mod; 74 } 75 for(i=full;~i;--i) 76 for(j=full;~j;--j) 77 if((i&j)==0)ans=(ans+f[i][j])%mod; 78 printf("%d\n",(ans+mod)%mod); 79 }
六,uoj372
刷新期望概率观的题目
思维难度不错,而且之前我是没见过期望概率用积分的……
虽然出题人说这很套路

1 #include <cstdio> 2 #include <cstring> 3 #define N 35 4 #define mod 998244353 5 #define N2 5000010 6 #define LL long long 7 #define RG register 8 #define MD 2332333 9 struct hash_map 10 { 11 struct node{int state,next,id;}s[N2]; 12 int e,adj[MD]; 13 inline void ins(int state,int id) 14 { 15 RG int pos=state%MD; 16 s[++e].state=state,s[e].next=adj[pos];adj[pos]=e;s[e].id=id; 17 } 18 inline int find(int state) 19 { 20 RG int i,pos=state%MD; 21 for(i=adj[pos];i;i=s[i].next) 22 if(s[i].state==state)return s[i].id; 23 return -1; 24 } 25 }H; 26 struct node 27 { 28 int A[N],n; 29 inline node operator * (const node &a)const 30 { 31 RG int i,j; 32 node c;memset(c.A,0,sizeof(c.A)); 33 c.n=n+a.n; 34 for(i=0;i<=n;++i) 35 for(j=0;j<=a.n;++j) 36 c.A[i+j]=(c.A[i+j]+(LL)A[i]*a.A[j])%mod; 37 return c; 38 } 39 }X[N2]; 40 int tot,T,vis[N],d[N][N],adj[N],C[N][N]; 41 int inv[N],inv2[N],bin[N],cnt1[65546],n,m,A[N],B[N]; 42 inline int count(int s){return cnt1[s&65535]+cnt1[s>>16];} 43 inline int dfs(RG int rt,int G) 44 { 45 RG int ret=bin[rt-1];vis[rt]=T; 46 for(RG int i=1;i<=n;++i) 47 if(vis[i]!=T&&d[rt][i]&&(G&bin[i-1]))ret|=dfs(i,G); 48 return ret; 49 } 50 inline void update(node &a,const node &b,int d) 51 { 52 RG int i,j,nn=b.n+d; 53 memset(A,0,sizeof(A)),memset(B,0,sizeof(B)); 54 for(i=0;i<=d;++i) 55 if(i&1)A[i]=mod-C[d][i];else A[i]=C[d][i]; 56 for(i=0;i<=b.n;++i)for(j=0;j<=d;++j) 57 B[i+j]=(B[i+j]+(LL)b.A[i]*A[j])%mod; 58 for(i=0;i<=nn;++i)a.A[i]=(a.A[i]+B[i])%mod; 59 } 60 inline int getans(RG int G) 61 { 62 int pre=H.find(G); 63 if(pre!=-1)return pre; 64 if(!G) 65 { 66 ++tot,X[tot].n=0,X[tot].A[0]=1;H.ins(G,tot); 67 return tot; 68 } 69 ++T,++tot,H.ins(G,tot); 70 RG int i,u,j,un=0,cid=tot; 71 int block[N]; 72 for(i=1;i<=n;++i) 73 if((G&bin[i-1])&&vis[i]!=T) 74 {u=dfs(i,G);if(u!=G)block[++un]=u;} 75 if(un) 76 { 77 for(X[cid]=X[getans(block[1])],i=2;i<=un;++i) 78 X[cid]=X[cid]*X[getans(block[i])]; 79 return cid; 80 } 81 X[cid].n=count(G); 82 for(i=1;i<=n;++i) 83 if(G&bin[i-1]) 84 update(X[cid],X[getans(G&(~adj[i]))],count(G&adj[i])-1);//考虑每个点作为最大值 85 86 for(i=X[cid].n;i;--i)X[cid].A[i]=(LL)inv[i]*X[cid].A[i-1]%mod;//求导 87 RG int sum=0; 88 for(i=X[cid].n;i;--i)sum=(sum+(LL)X[cid].A[i]*inv2[i])%mod;//求导第二部分 89 X[cid].A[0]=(mod+inv2[X[cid].n]-sum)%mod;//考虑最大值<=t/2 90 return cid; 91 } 92 int main() 93 { 94 RG int i,j,a,b; 95 scanf("%d%d",&n,&m); 96 for(bin[0]=i=1;i<=30;++i)bin[i]=bin[i-1]<<1; 97 for(inv[0]=inv[1]=1,i=2;i<=n+5;++i)inv[i]=(LL)(mod-mod/i)*inv[mod%i]%mod; 98 for(inv2[0]=1,i=1;i<=n+5;++i)inv2[i]=(LL)inv2[i-1]*inv[2]%mod; 99 for(i=1;i<=n;++i)adj[i]=bin[i-1]; 100 for(i=1;i<bin[16];++i)cnt1[i]=cnt1[i^(i&-i)]+1; 101 for(i=1;i<=m;++i) 102 scanf("%d%d",&a,&b),d[a][b]=d[b][a]=1,adj[a]|=bin[b-1],adj[b]|=bin[a-1]; 103 for(C[0][0]=1,i=1;i<=n+5;++i) 104 for(C[i][0]=1,j=1;j<=i;++j) 105 C[i][j]=(C[i-1][j-1]+C[i-1][j])%mod; 106 RG int fin=getans(bin[n]-1),ans=0; 107 for(i=0;i<=n;++i) 108 ans=(ans+(LL)inv[n+1]*X[fin].A[i])%mod; 109 for(i=0;i<=n;++i) 110 ans=(ans+(LL)inv[n-i+1]*X[fin].A[i]%mod*(bin[n-i+1]-1))%mod; 111 printf("%d\n",2-ans+mod); 112 }
七,codeforces848E
一开始想了个暴力dp,结果发现自己也漏了不少状态,也重了不少……
然后就很完蛋啊……发现没法打
最后怂了题解,然后题解和我一样先考虑一条弧的状态
但是又不太一样……他考虑的是“弧两端由对称的花分开”,然后枚举第一个对称的位置,统计乘积×方案数
我是直接统计一个半圆
然后最后枚举两个弧拼起来统计答案
这玩意……堆砖的工作……

1 #include <cstdio> 2 #include <algorithm> 3 #include <cstring> 4 #include <cstdlib> 5 using namespace std; 6 #define N 50010 7 #define L (1<<19)+10 8 #define mod 998244353 9 #define RG register 10 #define LL long long 11 int n,g[N],f0[N],f1[N],f2[N],pf[N]; 12 inline int quick_mod(int di,int mi) 13 { 14 RG int ret=1; 15 for(;mi;mi>>=1,di=(LL)di*di%mod) 16 if(mi&1)ret=(LL)ret*di%mod; 17 return ret; 18 } 19 int poww[L],rev[L],bin[25],logi[L],inv[L],len=1; 20 inline void dft(int *a,int ra,int opt) 21 { 22 RG int i,j,d=logi[len]-logi[ra],l,tmp,wn,*w,*x,*y; 23 for(i=0;i<ra;++i)if(i<(rev[i]>>d))swap(a[i],a[rev[i]>>d]); 24 for(d=2;d<=ra;d<<=1) 25 for(i=0,l=(d>>1),wn=(opt==1?(len/d):(-len/d));i<ra;i+=d) 26 for(j=0,x=a+i,y=x+l,w=poww+((opt==1)?0:len);j<l;++j,++x,++y,w+=wn) 27 tmp=(LL)(*w)*(*y)%mod,*y=(*x+mod-tmp)%mod,*x=(*x+tmp)%mod; 28 if(opt==-1) 29 for(i=0;i<ra;++i)a[i]=(LL)a[i]*inv[ra]%mod; 30 } 31 int tmp1[L],tmp2[L]; 32 inline int solve1(int l,int r) 33 { 34 if(l==r)return 1; 35 RG int i,mi=l+r>>1,ra=r-l+1,la=1,r1=solve1(l,mi); 36 while(la<(ra+r1))la<<=1; 37 for(i=0;i<r1;++i)tmp1[i]=f0[l+i]; 38 memset(tmp1+r1,0,la-r1<<2);dft(tmp1,la,1); 39 for(i=0;i<ra;++i)tmp2[i]=(LL)g[i]*pf[i]%mod; 40 memset(tmp2+ra,0,la-ra<<2);dft(tmp2,la,1); 41 for(i=0;i<la;++i)tmp2[i]=(LL)tmp2[i]*tmp1[i]%mod; 42 dft(tmp2,la,-1); 43 for(i=mi+1;i<=r;++i)f0[i]=(f0[i]+tmp2[i-l-1])%mod; 44 for(i=0;i<ra;++i)tmp2[i]=(LL)g[i]*pf[i+1]%mod; 45 memset(tmp2+ra,0,la-ra<<2);dft(tmp2,la,1); 46 for(i=0;i<la;++i)tmp1[i]=(LL)tmp2[i]*tmp1[i]%mod; 47 dft(tmp1,la,-1); 48 for(i=mi+1;i<=r;++i)f1[i]=(f1[i]+tmp1[i-1-l])%mod; 49 for(i=0;i<r1;++i)tmp1[i]=f1[l+i]; 50 memset(tmp1+r1,0,la-r1<<2);dft(tmp1,la,1); 51 for(i=0;i<la;++i)tmp2[i]=(LL)tmp2[i]*tmp1[i]%mod; 52 dft(tmp2,la,-1); 53 for(i=mi+1;i<=r;++i)if(i-l-3>=0)f0[i]=(f0[i]+tmp2[i-l-3])%mod; 54 for(i=mi+1;i<=r;++i)f2[i]=(f2[i]+tmp2[i-1-l])%mod; 55 for(i=0;i<ra;++i)tmp2[i]=(LL)g[i]*pf[i+2]%mod; 56 memset(tmp2+ra,0,la-ra<<2);dft(tmp2,la,1); 57 for(i=0;i<la;++i)tmp1[i]=(LL)tmp2[i]*tmp1[i]%mod; 58 dft(tmp1,la,-1); 59 for(i=mi+1;i<=r;++i)if(i-l-3>=0)f1[i]=(f1[i]+tmp1[i-l-3])%mod; 60 for(i=0;i<r1;++i)tmp1[i]=f2[l+i]; 61 memset(tmp1+r1,0,la-r1<<2);dft(tmp1,la,1); 62 for(i=0;i<la;++i)tmp2[i]=(LL)tmp2[i]*tmp1[i]%mod; 63 dft(tmp2,la,-1); 64 for(i=mi+1;i<=r;++i)if(i-l-3>=0)f2[i]=(f2[i]+tmp2[i-l-3])%mod; 65 solve1(mi+1,r); 66 return ra; 67 } 68 signed main() 69 { 70 RG int i; 71 scanf("%d",&n);while(len<(n<<2))len<<=1; 72 for(bin[0]=i=1;i<=20;++i)bin[i]=bin[i-1]<<1; 73 for(i=0;i<=18;++i)logi[bin[i]]=i; 74 for(inv[2]=((mod+1)>>1),i=2;i<=18;++i)inv[bin[i]]=(LL)inv[bin[i-1]]*inv[2]%mod; 75 for(i=0;i<len;++i) 76 if(i&1)rev[i]=(rev[i>>1]>>1)|(len>>1); 77 else rev[i]=rev[i>>1]>>1; 78 poww[0]=poww[len]=1,poww[1]=quick_mod(3,(mod-1)/len); 79 for(i=2;i<len;++i)poww[i]=(LL)poww[i-1]*poww[1]%mod; 80 for(i=1;i<=n+2;++i)pf[i]=(LL)i*i%mod; 81 g[0]=1,g[1]=0,g[2]=1,g[3]=0; 82 for(i=4;i<=n;i+=2)g[i]=(g[i-2]+g[i-4])%mod; 83 f0[0]=0,f1[0]=1,f2[0]=4; 84 for(i=1;i<=n;++i) 85 {f0[i]=(LL)g[i]*pf[i]%mod;f1[i]=(LL)g[i]*pf[i+1]%mod;f2[i]=(LL)g[i]*pf[i+2]%mod;} 86 solve1(0,n); 87 RG int ans=(LL)(g[n-1]+g[n-3])*pf[n-1]%mod*n%mod; 88 for(i=3;i<n;++i)ans=(ans+(LL)g[i-2]*pf[i-2]%mod*f0[n-i]%mod*(i-1))%mod; 89 for(i=3;i<n;++i)ans=(ans+(LL)2*g[i-3]*pf[i-2]%mod*f1[n-i-1]%mod*(i-1))%mod; 90 for(i=4;i<=n-2;++i)ans=(ans+(LL)g[i-4]*pf[i-2]%mod*f2[n-i-2]%mod*(i-1))%mod; 91 printf("%d\n",ans); 92 }
八,LOJ2331
2017清华集训的题目
从dalao们的博客来看,是最水的一道题?
那还是我太菜了233333……怼了好几天最后还是怂了题解
我一开始想的是分权值讨论,然后从大到小搞
然后一开始以为相同区间的可以合并,然后就是一个$v^{len}-(v-1)^{len}$
结果发现不太对……如果区间有重复的话就会完蛋
到最后这个贡献我也不会dp
发现我们可以离散之后分段考虑,一段之内的贡献是一样的
然后裸转移是$O(n)$的,可以通过前缀和然后搞个倍数乘除一下优化成$O(1)$
太神了……

1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 #define RG register 6 #define LL long long 7 #define mod 998244353 8 #define N 2010 9 inline int quick_mod(int di,int mi) 10 { 11 RG int ret=1; 12 for(;mi;mi>>=1,di=(LL)di*di%mod) 13 if(mi&1)ret=(LL)ret*di%mod; 14 return ret; 15 } 16 struct node 17 { 18 int l,r,val; 19 node(int a=0,int b=0,int c=0){l=a,r=b,val=c;} 20 }q[N],s[N]; 21 int tmp[N],keypt[N],len[N],pt[N]; 22 int lcnt,cnt,scnt,A; 23 int f[2][N],g[2][N],lim[N]; 24 int l[N],sl[N]; 25 int pre1[N],pre2[N],pre3[N],inv2[N],inv3[N]; 26 inline int dp(int val) 27 { 28 if(val==1)return 1; 29 RG int i,j,cur=0; 30 f[0][0]=g[0][0]=1;s[0].r=0; 31 pre1[0]=pre2[0]=pre3[0]=inv2[0]=inv3[0]=1; 32 for(i=1;i<=lcnt;++i) 33 { 34 g[0][i]=1,f[0][i]=0,sl[i]=sl[i-1]+l[i]; 35 pre1[i]=(quick_mod(val,l[i])-quick_mod(val-1,l[i])+mod)%mod; 36 pre2[i]=quick_mod(val-1,sl[i]);inv2[i]=quick_mod(pre2[i],mod-2); 37 pre3[i]=quick_mod(val,sl[i]);inv3[i]=quick_mod(pre3[i],mod-2); 38 } 39 for(i=1;i<=scnt;++i) 40 { 41 cur^=1; 42 for(j=0;j<s[i].l;++j)f[cur][j]=g[cur][j]=0; 43 for(j=s[i].l;j<=s[i].r;++j) 44 { 45 f[cur][j]=f[cur^1][j]; 46 if(j>s[i-1].r) 47 f[cur][j]=(f[cur][j]+ (LL)g[cur^1][s[i-1].r] * pre2[s[i-1].r] %mod * pre3[j-1] %mod * inv3[s[i-1].r] %mod * pre1[j] )%mod; 48 g[cur][j]=(g[cur][j-1]+(LL)f[cur][j]*inv2[j])%mod; 49 } 50 for(j=s[i].r+1;j<=lcnt;++j)g[cur][j]=g[cur][j-1],f[cur][j]=0; 51 } 52 return (LL)g[cur][lcnt]*pre2[lcnt]%mod; 53 } 54 inline bool mt(const node &a,const node &b) 55 {return a.val==b.val?a.r<b.r:a.val<b.val;} 56 inline void work() 57 { 58 RG int i,j,n,m,a,b,val,ge=0,ans; 59 scanf("%d%d%d",&n,&m,&A); 60 for(i=1;i<=m;++i) 61 { 62 scanf("%d%d%d",&a,&b,&val); 63 q[i]=node(a,b,val); 64 tmp[++ge]=a,tmp[++ge]=b; 65 } 66 tmp[++ge]=1,tmp[++ge]=n; 67 sort(tmp+1,tmp+ge+1),ge=unique(tmp+1,tmp+ge+1)-tmp-1; 68 for(cnt=0,i=1;i<=ge;++i) 69 { 70 keypt[++cnt]=tmp[i],len[cnt]=1; 71 if(i<ge&&tmp[i]+1<tmp[i+1]) 72 keypt[++cnt]=tmp[i]+1,len[cnt]=tmp[i+1]-tmp[i]-1; 73 } 74 sort(q+1,q+m+1,mt); 75 bool can;RG int v,maxn; 76 memset(lim,0,sizeof(lim)); 77 for(i=1;i<=m;++i) 78 { 79 q[i].l=lower_bound(keypt+1,keypt+cnt+1,q[i].l)-keypt; 80 q[i].r=lower_bound(keypt+1,keypt+cnt+1,q[i].r)-keypt; 81 for(can=0,maxn=0,j=q[i].l;j<=q[i].r;++j) 82 if(!lim[j])lim[j]=q[i].val,can=1; 83 else maxn=max(maxn,lim[j]); 84 if(!can&&maxn<q[i].val){puts("0");return;} 85 } 86 ans=1; 87 for(i=1;i<=m;) 88 { 89 for(scnt=0,v=q[i].val,j=i;v==q[j].val&&j<=m;++j)s[++scnt]=q[j]; 90 for(i=j,lcnt=0,j=1;j<=cnt;++j) 91 if(lim[j]==v)l[pt[j]=++lcnt]=len[j]; 92 for(j=1;j<=scnt;++j) 93 { 94 while(lim[s[j].l]!=v)++s[j].l; 95 while(lim[s[j].r]!=v)--s[j].r; 96 s[j].l=pt[s[j].l],s[j].r=pt[s[j].r]; 97 } 98 ans=(LL)ans*dp(v)%mod; 99 } 100 for(i=1;i<=cnt;++i) 101 if(!lim[i])ans=(LL)ans*quick_mod(A,len[i])%mod; 102 printf("%d\n",ans); 103 } 104 int main() 105 { 106 RG int i,j,t; 107 scanf("%d",&t); 108 while(t--)work(); 109 }
九,LOJ2330
依然是清华集训的题目
依旧没做出来
依旧怂了题解
我们从第三个部分分开始考虑,只输出根的答案
什么样的情况下能有答案呢?
相当于我们要把儿子们分成两半,让他们数量一样
并且能够互相抵消,最后让心停在根节点
那么……肯定是最大的那个儿子最难被抵消
我们考虑最大的那个儿子有多大
然后看其他儿子能不能把它抵消掉
我们定义$f(i)$为以$i$为根的子树最多能抵消多少对生长的贡献
如果一个点子树大小是偶数,
那么我们考虑最大的那个子树,我们肯定优先把它消掉
如果它能被消掉,我们其他子树里的就可以对着叉,怎么叉都可以叉掉
那么我们考虑,优先让这个最大的子树$s1$自相残杀,再用其他儿子来帮他
最多能消掉最大子树的节点数就是$size[rt]-1-size[s1]+f[s1]*2$
那么如果这个数大于等于$size[s1]$,这个树就可以全部消掉,$f[rt]=(size[rt]-1)/2$
而对于处理不是根的点,我们把根到它缩成一条路径,这样和刚才计算根是一样的
然后就可以打了,复杂度是$O(Tn)$的

1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 #define RG register 5 #define N 100010 6 char B[1<<15],*S=B,*T=B; 7 #define getc (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++) 8 inline int read() 9 { 10 RG int x=0;RG char c=getc; 11 while(c<'0'|c>'9')c=getc; 12 while(c>='0'&c<='9')x=10*x+(c^48),c=getc; 13 return x; 14 } 15 int W,n,e,adj[N]; 16 struct edge{int zhong,next;}s[N<<1]; 17 inline void add(int qi,int zhong) 18 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 19 int ans[N],size[N],maxn[N],son1[N],son2[N]; 20 inline void dfs1(int rt,int fa) 21 { 22 size[rt]=1;son1[rt]=son2[rt]=0; 23 for(RG int u,i=adj[rt];i;i=s[i].next) 24 if((u=s[i].zhong)!=fa) 25 { 26 dfs1(u,rt);size[rt]+=size[u]; 27 if(size[u]>size[son1[rt]])son2[rt]=son1[rt],son1[rt]=u; 28 else if(size[u]>size[son2[rt]])son2[rt]=u; 29 } 30 if(son1[rt]) 31 { 32 RG int left=size[rt]-1-size[son1[rt]]; 33 if(size[son1[rt]]<=left+(maxn[son1[rt]]<<1))maxn[rt]=size[rt]-1>>1; 34 else maxn[rt]=maxn[son1[rt]]+left; 35 } 36 } 37 inline void dfs2(int rt,int fa,int dep,int maxson) 38 { 39 if((n-dep)&1)ans[rt]=0; 40 else 41 { 42 RG int bs=((size[maxson]>size[son1[rt]])?maxson:son1[rt]); 43 ans[rt]=(size[bs]<=n-dep-size[bs]+(maxn[bs]<<1)); 44 } 45 for(RG int u,i=adj[rt];i;i=s[i].next) 46 if((u=s[i].zhong)!=fa) 47 if(u==son1[rt])dfs2(u,rt,dep+1, (size[maxson]>size[son2[rt]])?maxson:son2[rt]); 48 else dfs2(u,rt,dep+1, (size[maxson]>size[son1[rt]])?maxson:son1[rt]); 49 } 50 inline void work() 51 { 52 RG int i,a,b; 53 n=read(); 54 e=0;memset(adj,0,n+1<<2); 55 memset(son1,0,n+1<<2); 56 memset(son2,0,n+1<<2); 57 for(i=1;i<n;++i) 58 a=read(),b=read(),add(a,b),add(b,a); 59 dfs1(1,0);dfs2(1,0,1,0); 60 if(W==3)printf("%d",ans[1]); 61 else for(i=1;i<=n;++i)printf("%d",ans[i]); 62 printf("\n"); 63 } 64 int main() 65 { 66 W=read();int t=read(); 67 while(t--)work(); 68 }
十,codeforces379E
这题的动归定义其实没那么难
但是……这是个仙人掌啊……仙人掌啊……
所以代码实现就特别完蛋了
我想的是把每个环拆成链,维护链顶链底的状态
打了180行还是错的,细节还贼多
这就比较坑了……于是我找了个标程,发现人家和我的定义一样
但是只有我傻傻的手动分类讨论,人家用for循环枚举加几个简单的ifelse判断就行了
于是深刻的研究了一下std……仙人掌的题目我还的确没做过,这题是不错的入门(?)题
code:

1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 #define RG register 5 #define inf 0x3f3f3f3f 6 #define N 2510 7 inline int max(int a,int b){return a>b?a:b;} 8 int n,m,e,adj[N]; 9 struct edge{int zhong,next;}s[N<<2]; 10 inline void add(int qi,int zhong) 11 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 12 int size[N],f[N][N][3][3],vis[N],top[N]; 13 int g[N][3][3]; 14 inline void dfs(int rt,int fa) 15 { 16 size[rt]=1; 17 ++vis[rt]; 18 f[rt][0][0][0]=f[rt][1][1][0]=0,f[rt][0][2][0]=1; 19 bool isend=0; 20 for(RG int u,i=adj[rt];i;i=s[i].next) 21 { 22 if(vis[u=s[i].zhong]<2&&u!=fa) 23 if(!vis[u]) 24 { 25 dfs(u,rt); 26 memset(g,-0x3f,sizeof(g)); 27 if(top[u]) 28 { 29 if(top[u]==rt) 30 { 31 for(RG int j=size[rt];~j;--j) 32 for(RG int k=size[u];~k;--k) 33 for(RG int a=0;a<3;++a) 34 for(RG int b=0;b<3;++b)if(a^b^3) 35 for(RG int c=0;c<3;++c) 36 g[j+k][a][c]=max(g[j+k][a][c],f[rt][j][a][c]+f[u][k][b][a]); 37 } 38 else 39 { 40 top[rt]=top[u]; 41 for(RG int j=size[rt];~j;--j) 42 for(RG int k=size[u];~k;--k) 43 for(RG int a=0;a<3;++a) 44 for(RG int b=0;b<3;++b)if(a^b^3) 45 for(RG int c=0;c<3;++c) 46 g[j+k][a][c]=max(g[j+k][a][c],f[rt][j][a][0]+f[u][k][b][c]); 47 } 48 } 49 else 50 { 51 for(RG int j=size[rt];~j;--j) 52 for(RG int k=size[u];~k;--k) 53 for(RG int a=0;a<3;++a) 54 for(RG int b=0;b<3;++b)if(a^b^3) 55 for(RG int c=0;c<3;++c) 56 g[j+k][a][c]=max(g[j+k][a][c],f[rt][j][a][c]+f[u][k][b][0]); 57 } 58 size[rt]+=size[u]; 59 for(RG int j=size[rt];~j;--j) 60 for(RG int a=0;a<3;++a) 61 for(RG int b=0;b<3;++b) 62 f[rt][j][a][b]=g[j][a][b]; 63 } 64 else isend=1,top[rt]=u; 65 } 66 if(isend) 67 for(RG int i=0;i<=size[rt];++i) 68 { 69 for(RG int a=0;a<3;++a)f[rt][i][a][2]=f[rt][i][a][1]=f[rt][i][a][0]; 70 f[rt][i][1][2]=f[rt][i][2][1]=-inf; 71 } 72 ++vis[rt]; 73 } 74 int main() 75 { 76 // freopen("Ark.in","r",stdin); 77 RG int i,a,b; 78 scanf("%d%d",&n,&m); 79 for(i=1;i<=m;++i) 80 scanf("%d%d",&a,&b),add(a,b),add(b,a); 81 memset(f,-0x3f,sizeof(f)); 82 dfs(1,0); 83 for(i=0;i<=n;++i) 84 printf("%d ",max(max(f[1][i][0][0],f[1][i][1][0]),f[1][i][2][0])); 85 }
十一,codeforces804F
这题太神了!!!!!
膜拜出题的伊朗神犇
题目显然可以分成两问,第一部分统计最后都有谁能拿到假金块
第二部分用第一部分的结果统计答案
可是我两个部分都不会啊
这可怎么办呢
然后在思考半个多小时无果的情况下我打开了题解
看了快俩小时才看懂那是什么……
大概的推导过程是这样的:
首先我们考虑两个被有向边链接的点$u$和$v$,设其大小为$s_{u}$和$s_{v}$,定义$g=gcd(s_{u},s_{v})$
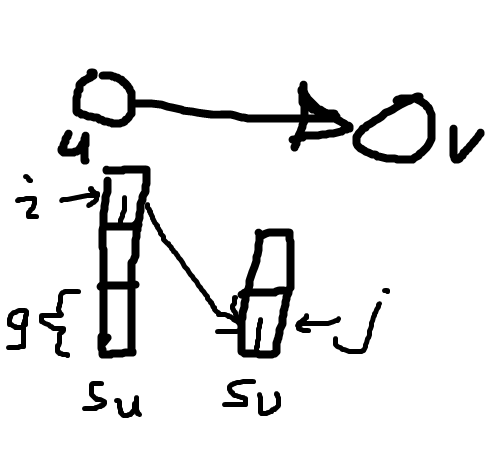
那么如果$i \% g == j \% g$,那么i和j之间应该有边,即“如果i有金块,那么i会给j一个假金块”
这样的贡献是很显然的。那么我们来考虑复杂一点的情况:如果有链$u->v->w$,现在我们考虑$u$对$w$的贡献。
图中定义$g=gcd(s_{u},s_{v})$:
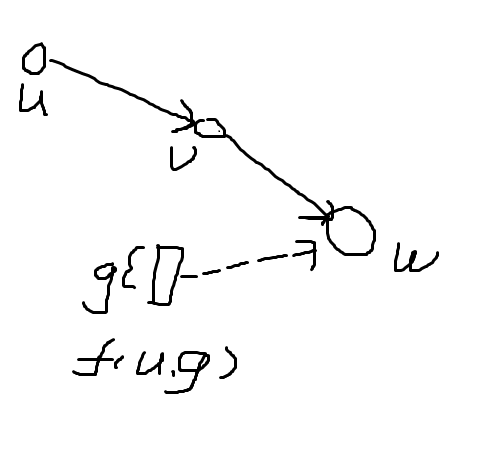
我先解释一下新出现的f是啥:
我们定义$f(v,g)$为一个假想帮派,其大小为$g$,并且满足如果帮派$v$中第$i$个人有金块,那么$f(v,g)$中第$i\%g$个人就有金块
这样的话,由于u对w的贡献应该体现在“u使v出现了v自己没有的金块,然后v又把这个金块给了w”
那么我们$u$对$w$的贡献就可以体现为一个$f(u,gcd(s_{u},s_{v}))$对$w$的贡献
这样也不难理解……因为如果v用从u那里拿到的金块去贡献w,那贡献的单元一定是$f(u,gcd(s_{u},s_{v}))$
那么我们推广一下:假如有一条链$w_{1}->w_{2}->......->w_{n}$,
那么$w_{1}$对$w_{n}$的贡献应该可以体现为$f(w_{1},gcd(s_{w_{1}},s_{w_{2}},.....s_{w_{n-1}}))$
但是原图并不保证是个$DAG$,所以我们考虑,如果有一个闭合回路$v->w_{1}->w_{2}->......->w_{n}->v$,
那么$v$对自己的贡献是什么呢?
类比上面的做法,应该可以体现为$f(v,gcd(s_{v},s_{w_{1}},s_{w_{2}},.....s_{w_{n}}))$
那么我们现在可以处理环内部的贡献了,那么我们考虑把环缩成点,考虑整体对其他联通块的贡献
结合刚才我们的定义,现在我们应该有一个对于某个环定义的$h(S,g)$,
依然是大小为g的帮派,但是现在只要强连通分量S中有某一个元素$w_{i}$中存在i有金块,那么h中$i\%g$就有一个金块
在定义了h之后,我们计算环中的答案也容易了:对于$S$中帮派v,如果$h(S,g)$中第i个有金块,那么所有$v_{j}(j\%g==i)$都会有金块,
因为环上每个点也会被这个环所有点进行贡献
再考虑$SCC$之间的贡献:我们缩完点之后,原图变成了$DAG$完全图
那么这样的图里面一个存在一条哈密顿路径,即经过所有点的路径。这是很显然的。
那么我们按拓扑序遍历这个路径,每次用前面一个$SCC$的$h$去贡献后面一个$SCC$的$h$
这样我们就得到了最后的每个$h$,再按刚才说的方法统计就可以求出每个帮派最多有多少金块了
那么对于每个帮派,我们现在得到了它最少&最多可以卖出多少金块,分别定义为$mn$和$mx$
然后考虑统计答案,我们枚举每个帮派$v$作为被逮捕的$b$个帮派中实力最小的进行统计,
首先值得注意的是,我们这时候固定每个帮派的实力就是它能卖出的最多的金块
因为如果对于某种前a个的方案中,有的帮派没有卖出$mx$个,那么我们可以把他们换成卖出$mx$个,这样a集合是不变的。
所以我们就钦定帮派们都卖出了mx个
那么我们考虑另外一个帮派$u$,如果……
$mn_{u}>mx_{v}$,那么u一定实力比v大,设这样的一共有c1个帮派
$mx_{u}>mx_{v}$,那么u可能实力比v大,设这样的一共有c2个帮派(这里,当$mx$相等的时候,我们按照编号大小比较,这样就不重不漏了)
所以我们枚举有几个可能比v实力大的帮派最后被选中,设个数为$j$
那么对答案的贡献就是$C(c2,j)*C(c1,b-1-j)$
我们只要限制好枚举边界($j<b,j<=c2,j+c1<a$)就可以统计答案了
这样我们就解决了这道神题!
这题给我的触动是不小的……
第一部分推导的思路非常清晰,从简单情况发现规律,辅助变量$f$和$h$的引入,一条边到链到环的推导……这样的推导真的让人感觉非常畅快。
还有第二部分的统计答案,巧妙的枚举了实力最小的帮派,使得统计变得轻松。
这题目真的是666啊……
最后附上code:

1 #include <cstdio> 2 #include <cstring> 3 #include <vector> 4 using namespace std; 5 #define RG register 6 #define N 5010 7 #define mod 1000000007 8 #define LL long long 9 #define min(x,y) ((x)<(y)?(x):(y)) 10 char B[1<<15],*S=B,*T=B; 11 #define getc (S==T&&(T=(S=B)+fread(B,1,1<<15,stdin),S==T)?0:*S++) 12 inline int read() 13 { 14 RG int x=0;RG char c=getc; 15 while(c<'0'|c>'9')c=getc; 16 while(c>='0'&c<='9')x=10*x+(c^48),c=getc; 17 return x; 18 } 19 inline int get01() 20 { 21 RG char c=getc; 22 while(c<'0'|c>'1')c=getc; 23 return c^48; 24 } 25 int n,a,b,ge[N],e,adj[N]; 26 vector<int>mem[N],con[N],can[N]; 27 struct edge{int zhong,next;}s[N*N>>1]; 28 inline void add(int qi,int zhong) 29 {s[++e].zhong=zhong;s[e].next=adj[qi];adj[qi]=e;} 30 int dfn[N],low[N],num,sta[N],top; 31 int sz[N],belong[N],tot,mn[N],mx[N],C[N][N]; 32 inline int gcd(int a,int b){return b==0?a:gcd(b,a%b);} 33 #define vi vector<int>::iterator 34 inline void tarjan(int rt) 35 { 36 RG int i,u; 37 dfn[rt]=low[rt]=++num;sta[++top]=rt; 38 for(i=adj[rt];i;i=s[i].next) 39 if(!dfn[u=s[i].zhong])tarjan(u),low[rt]=min(low[rt],low[u]); 40 else if(!belong[u])low[rt]=min(low[rt],dfn[u]); 41 if(dfn[rt]==low[rt]) 42 { 43 ++tot; 44 do belong[u=sta[top--]]=tot,sz[tot]=gcd(sz[tot],ge[u]),con[tot].push_back(u);while(u!=rt); 45 can[tot].resize(sz[tot]); 46 for(vi it=con[tot].begin();it!=con[tot].end();++it) 47 for(vi j=mem[*it].begin();j!=mem[*it].end();++j) 48 can[tot][*j % sz[tot]]=1; 49 } 50 } 51 int main() 52 { 53 // freopen("Ark.in","r",stdin); 54 RG int i,j,x,ans=0,cnt1,cnt2; 55 n=read();a=read();b=read(); 56 for(i=1;i<=n;++i)for(j=1;j<=n;++j)if(get01())add(i,j); 57 for(i=1;i<=n;++i) 58 for(ge[i]=read(),j=0;j<ge[i];++j) 59 if(get01())++mn[i],mem[i].push_back(j); 60 for(i=1;i<=n;++i)if(!dfn[i])tarjan(i); 61 for(i=tot;i>1;--i) 62 for(sz[i-1]=gcd(sz[i],sz[i-1]),j=0;j<sz[i];++j) 63 if(can[i][j])can[i-1][ j % sz[i-1] ]=1; 64 for(i=1;i<=n;++i) 65 for(x=belong[i],j=0;j<ge[i];++j) 66 mx[i]+=can[x][j%sz[x]]; 67 for(C[0][0]=i=1;i<=n;++i) 68 for(C[i][0]=j=1;j<=i;++j) 69 C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; 70 for(i=1;i<=n;++i) 71 { 72 for(cnt1=0,j=1;j<=n;++j)if(mn[j]>mx[i])++cnt1; 73 if(cnt1>=a)continue; 74 for(cnt2=0,j=1;j<=n;++j) 75 if(mn[j]<=mx[i]&&(mx[j]>mx[i]||(mx[j]==mx[i]&&j>i)))++cnt2; 76 for(j=min(b-1,min(cnt2,a-cnt1-1));j>=0;--j) 77 ans=(ans+(LL)C[cnt2][j]*C[cnt1][b-1-j])%mod; 78 } 79 printf("%d\n",ans); 80 }
十二,总结
其实还有很多很棒的题目没有来得及写详细的题解
但是……接下来还要去盐焗其他知识,没有时间了,就凉凉了……
在这里做个小总结……
dp问题大概分为两类,计数和最优化,没了:)
写一些零散的思路吧
dp我们首先要有个状态
怎么设计状态是困扰广大OIER的千古难题
所以我也不会23333
不过一般来说,我们dp要找一些关键的量进行限制
一般限制的这些量会对结果产生影响……之类的
比如很多序列上的问题定义“最后一个在i”等等
我记得之前看见过一句很好的话:
“对于很多构造题和dp题,不妨先想想最优解是什么样子的,看看它有什么特征,再考虑如何设计状态&转移”
计数题的最大套路就是容斥了……
感觉容斥原理的应用可以“以时间换思考难度”,
使得本来根本没法处理的限制变得可做
同时,容斥原理在很多题目中还是正确性的保证
比如:
uoj193的环套树计数我们要枚举叶子,
但是可能剩下的点在有的联边情况下也变成了叶子,于是要容斥
uoj37的DAG计数同理,
枚举入度为0的点之后我们也不知道剩下的点里面有没有入度为0的点,于是要容斥
与容斥相对的处理方法就是考虑“计数如何不重不漏”了
这个就要用心考察每一个变量,看看枚举什么可以区分每一种状态了……
很难说这个东西具体怎么用,但是我感觉在做了上面两个uoj之后有一点点容斥的手感了
对于所有题目都可能适用的方法:正难则反(或者叫补集转换?)
第一次具体意识到“正难则反”是看到clj老师的计数pdf的时候
那些题目真的把我碾爆了QAQ
有的时候,如果我们正着处理合法(不合法)不好处理,而总状态很好计算,
我们就可以思考反过来处理不合法(合法)状态能不能行,然后就没准能做了
比较经典的是uoj37,这个题从正着dp“对于某个点集,其诱导子图的SCC数量”转换成了反着dp缩点之后DAG的方案数
还有昨天看的wc2007石头剪刀布,不直接统计三元环而是反过来统计$C(n,3)-cnt$(不是三元环)
对于所有题目都可能适用的方法:模型转换
这个就更加玄乎了
一般是从原本的问题,寻找其等价问题进行处理,从而简化问题
大多数时候,我们根本不知道如何模型转换
但是就算是咸鱼我们也要赌一赌国运
联想一下题目中的某些条件能不能换成别的等价的问题然后处理
我印象中最典型的就是权值转计数类问题了
我们给予题设权值一个实际意义,然后就把难处理的权值转成了计数问题
比如有一次模拟赛,权值是“len×cnt1”,我们就计数“任选一个染绿,再任选一个1染红(可重复染色),那么方案数就是len×cnt1
还有一次是权值是数量的平方,于是我们转换成二元组计数,维护两个独立的状态,
他们可以分别转移,最后答案就是平方后的结果
还有uoj193,这个权值定义是“环套树非叶子节点个数”,
我们就计数“每个点可以染黑白两种颜色,叶子只能染白”的数量,
然后正难则反枚举黑叶子集合容斥
这种转换似乎很常见的……但是该想不出来还想不出来
网格图利器:插头dp(轮廓线)
很多时候一个轮廓线干上去我们就会发现转移特别舒服
个人感觉常用于“需要决策每个格子放什么”的问题
不一定只用于传统的逐格转移
我们可以维护已选集合的轮廓(HEOI2018D1T1),也可以按行转移
总之网格图上轮廓线还是有前途的233
期望概率怎么做?
首先一个抓手就是期望的线性性
比如,很多题目都定义“在第i轮还没有结束的概率”,
然后利用期望的线性性加起来这就是期望轮数
还有一个就是积分的应用
以及前后缀不一定用于优化dp,状态定义里使用前后缀也许可以写出方便转移的式子
这次没做到期望概率的题目,还需要加强啊……
有一个很清真的想法就是“对于任何东西都可以定义函数”
不一定dp只能对下标定义啊……
比如我可以对于一张图定义一个函数,然后这个函数能够转移之类的
也就是说,我把所有东西都看成元素,这样也许能找到元素之间的关系来转移
数据范围极小怎么办?
我们还是别想爆搜了233333
那么我们一般考虑状压
状压的好帮手就是容斥(子集反演)啦
最近发现了状压的新套路
比如,当状态集合有2个,但是我们能发现包含关系的时候,可以压成3进制来做/直接哈希表硬上
以及一些小科技:fwt;枚举子集;用lowbit枚举所有的1而不是直接枚举判断是不是1
差分的应用也是特别6的
从原来的序列转换成维护差分数组,可能大大减少可能状态/维护难度
比如说单调的前后缀最值,以及一些单调不降的数组,我们可以用其差分值代表原序列
很大的可能就是变成了01然后可以状压了
权值范围很小,还和二进制有关?按位考虑也许是个好方法
数学(gcd,根号相关)dp题?想跟根号有关的性质,找到突破口
如果题设目标是对环上东西的一个DP,有一种可能的状态定义是
“对于一段圆弧(把环拆成链),其两端的状态分别是xx和yy的计数/最优解”
第一次见到这种想法是在cf848e上
今天听wq讲了bzoj3746加深了一点点印象
但是感觉如果遇到题还是可能想不起来啊……
这其实就把原来环上的问题简化为序列了,就可以用类区间dp的方法dp了
优化方法:改变数组定义
改变数组定义……看命了,能不能想出来的确是智商的问题
优化方法:辅助数组/预处理
有的时候我们会觉得dp细节很多,手动讨论很烦?
曾经我见过的一个不错的方法就是写4个calc函数然后来回来去的调用
这样的话代码非常简洁,并且思路也很清晰
我觉得个人的一大缺点就是太喜欢手动讨论了
这样的话代码会很长,细节也更多更不容易调试
所以……要多试着改变这一点
优化方法;决策单调性(单调队列/栈,四边形不等式)
这个方法似乎我分配的科技点比较少23333
太玄了,也说不好什么就一定能用,什么就一定不能用
需要我们观察转移方程,有单调性就能用呗……
优化方法:log((cdq)分治,(wqs)二分/三分)
其实二分三分算是决策单调性?
这样一般可以把原本的$n^{2}$变成$nlogn$,非常优秀
upd:2018-4-17
今天考试的T1(loj6032)非常不错
提示我们还有一种可行的模型转化方法是建立分治结构/重构树
我能想到的应用是克鲁斯卡尔重构树,最小割树,以及多点最短路
比如这个dp,就是把原来的序列建成重构树,
利用“建出来的区间两侧隔板高度都比它高,不用考虑边界”这一优秀性质来dp
同时wq想到的处理方法也是非常不错的:把条件和隔板一起排序,
直接找到每个条件对应在哪个节点被利用
优化方法;矩阵乘法(自动机)/倍增/特征多项式
如果我们发现dp过程和当前位置i没有什么关系,即每一步的转移都是类似的
那么我们可以考虑用上面的方式来加速转移
优化方法;前后缀和,卷积
这个有时候可以通过化简/变形dp转移方程发现特定形式,从而发现优化方法
优化方法:数据结构
打着打着就发现从dp题变成了数据结构题23333
不过有的时候用数据结构的确可以从枚举转移变成直接查询转移,优化复杂度
大概用于“用来转移的状态处于一个连续区间”的时候
十三,题表
按推荐等级排序~(level大的更加666)
$Level 6$ 共11题 强力推荐
uoj37 uoj193 uoj316 uoj372
bzoj3746 codechef_SEPT11_CNTHEX
cf804F cf855G cf923G cf865E
TopCoder_SRM_641_Hard(有兴趣可以考虑一下加强版问题:n<=1e5)
$Level 5$ 共11题
cf848e cf814E cf938F bzoj3326
uoj141 uoj348 loj553 bzoj1435
Topcoder_SRM_639_Div1_Level2
Topcoder_SRM_547_Div1_Level3
bzoj4871
$Level 4$ 共13题
loj2330 loj2331 bzoj4712 bzoj4513
cf903F cf814D cf755G cf379G uoj370
cf917C cf917D cf722E cf590D
$Level 3$ 共5题
loj2325 uoj129 uoj110 uoj300
uoj139 hihoCoder_challenge_19A/1279
$Level 2$ 共1题
loj6301
$Level 1$ 共1题
cf814C
$Unrated$
(我没有做也没有想所以没办法评级咯……)
hdu4809 51nod1684 loj2450 bzoj3830
bzoj3711 bzoj3717 bzoj2216 bzoj2091
bzoj3831 hdu5513 loj6274 uoj140
cf773f uoj11 cf468e bzoj4036
bzoj4557 bzoj4859 bzoj4818 loj520
loj2321 loj2324 loj2180 loj2255
loj530 loj515
final update:2018-4-17 16:08:31



 浙公网安备 33010602011771号
浙公网安备 33010602011771号