『学习笔记』图的基本应用
\(\textsf{update on 2022/6/18 修补了不足之处,修改码风,增加了推荐习题。}\)
什么是图
图 (\(Graph\)),是顶点 (\(Vertex\)) 和边 (\(Edge\)) 的集合。
图分为有向图和无向图,带权图和无权图。
- 有向图:边是有方向的,即只能单向通行。
- 无向图:边是双向的,即可以双向通行。
- 带权图:边是带权的,即每条边都有一个特定的值 \(w\)。
- 无权图:每条边的权值都为 \(1\)。
图的相关概念:
- 路径:从顶点 \(u\) 到顶点 \(v\) 的一种方案,即通过任意条边从 \(u\) 到达 \(v\)。
- 连通图:任意两个顶点之间都有至少一条路径。
- 子图:故名思意,当一个图 \(H\) 是图 \(G\) 的子集时,那么称 \(H\) 是 \(G\) 的子图。
- 二分图:图被分为两个子集,每个子集的顶点互不相交,即没有边连接同一个子集中的顶点。
- 稀疏图:即顶点较多,而边很少的图,顶点和边的比较小。
- 稠密图:与稀疏图相反,顶点和边的比较大。
一般情况下,图的顶点数设为 \(n\),边数设为 \(m\),输入边时,输入 \(u\ v\ w\) 表示有一条边从 \(u\) 连向 \(v\),权值为 \(w\)。
图的存储
邻接矩阵
定义一个 \(n \times n\) 的矩阵 \(g\),\(g_{u,v}\) 表示顶点 \(u\) 和顶点 \(v\) 之间边的权值,如果顶点之间没有边,则为 \(0\)。每个顶点与自己的距离为 \(0\),即 \(g_{u,u}=0\)。
若是无权图,那么如果 \(g_{u,v}\) 有连边,那么 \(g_{u,v}=1\)。
以这样一张无向无权图为例:
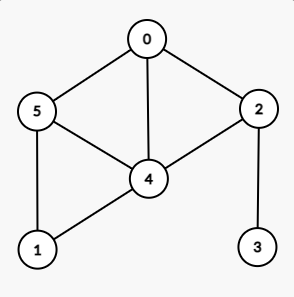
那么对应的邻接矩阵就是:
可以发现,无向图的邻接矩阵中,沿正对角线对称。
邻接矩阵代码(有向带权图):
#include <iostream>
using namespace std;
const int N=1e3+5; // 顶点数最大为1000
int n,m,u,v,w;
int g[N][N]; // 邻接矩阵存图
int main(){
// n个点,m条边
cin >> n >> m;
while(m--){
// 依次输入m条边
// 从顶点u到顶点v有一条权值为w的边
cin >> u >> v >> w;
g[u][v]=w;
}
// do something
return 0;
}
邻接矩阵的空间复杂度为 \(\mathcal{O}(n^2)\),所以只能存储较小的图。它的空间复杂度太大了,所以很多情况下都不会使用。
邻接表
这是一种更优的存图方式,优化了邻接矩阵,将为每个顶点建立的与其它顶点的关系数组改为链表,只存储和当前顶点之间有连边的顶点。对于稀疏图来说,有很大的优势。
还是那张图,来看一看它的邻接表存储:

存储为:
注意,每个链表中的顶点是独立的,只跟这个顶点有关系,跟别的顶点没半点关系。不要将箭头误解为边。每个顶点都有一个对应的链表,这个链表存储了与顶点相连的所有顶点编号。可以将上面的 \(\rightarrow\) 看作逗号。
那么如何存储带权图呢?
考虑这张图:
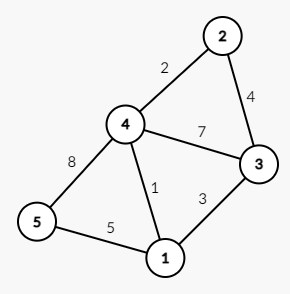
那么链表的每个结点就要记录两个值了:连接的顶点,连接的某个顶点的边的权值。
邻接表如下:
就是这么简单,对于链表,我们使用 STL 中的 vector 存储,每个节点需要两个值,使用 pair<int,int>,下面是一个存储有向带权图的程序:
#include <iostream>
#include <vector>
using namespace std;
const int N=1e3+5; // 最大顶点数:1000
int n,m,u,v,w;
vector<pair<int,int>> g[N]; // 邻接表存图
int main(){
cin >> n >> m;
while(m--){
cin >> u >> v >> w;
g[u].push_back(make_pair(v,w)); // 存边
// pair<到达的顶点编号,边权>
}
// do something
return 0;
}
这种存图方式相比邻接矩阵占用空间少多了,但还存在一个问题:如果一个顶点没有与任何顶点相连,那么这个顶点的 vector 就多占了一些空间,还有一种更优的存图方式:链式前向星。
链式前向星
就是直接用链表代替 vector,省去了不必要的空间,常数更小。
用一个数组 \(e\) 存储所有边,类型为边的类型 edge。
edge 中包含:
to:这条边指向的顶点。nxt:这条边之前输入的一条从同一顶点出发的边在数组 \(e\) 中的下标。val:视情况而定,如果是带权图,那么就有这一项。表示边权。
然后再定义一个数组 \(head\),存储每个顶点的最后一条边在 \(e\) 中的下标。
先来看看如何加边吧。
void add(int u,int v,int w){ // 传入一条边,参数分别为起始顶点,指向顶点,边权
top++; // 边的总数+1
e[top].to=v; // 这条边通向的是 v
e[top].val=w; // 这条边的边权
e[top].nxt=head[u];
// head[u] 即为上一个输入的,起始顶点与当前边相同的边在 e 中的下标
// nxt 连向 head[u] 的作用便是让我们遍历某个顶点的所有出边时,可以找到上一条出边,还可以通过上一条出边找到上上条,直到遍历了所有出边
head[u]=top; // 既然又输入了一条,那么由顶点 u 出发的所有边中最后输入的一条就是当前这条边了
}
举个例子吧,依次输入了(每个括号中依次为 \(u,v,w\),即为起始顶点,到达顶点,边权):
\((1,3,4),(1,2,4),(1,5,1),(1,3,6)\)。
本例中,这些边的起始顶点都为 \(1\),只是为了方便模拟过程。输入中其中若有其它起始顶点,也是一样的道理。
head 数组初值全部为 \(0\),显然某个起始顶点第一条出边的 nxt 就为 \(0\)。
- 输入 \((1,3,4)\):这时输入了第 \(1\) 条边。\(e_1\) 通向的是顶点 \(3\),边权是 \(4\),由于是第一条边,
nxt为 \(0\),即表示没有上一条边。 - 输入 \((1,2,4)\):第 \(2\) 条边,\(e_2\) 通向的顶点为 \(2\),边权也是 \(4\),但起始顶点是同一个的,上一个输入的边在 \(e\) 中的下标为 \(1\) (\(head_1\) 存着),
nxt自然指向 \(1\)。 - 输入 \((1,5,1)\):第 \(3\) 条起始顶点为 \(1\) 的边,存储在 \(e_3\)。通向顶点 \(5\),权值 \(1\),上一条同一起始顶点相同的边就在隔壁 \(e_2\),所以
nxt为 \(2\)。 - 输入 \((1,3,6)\):假设在输入这条边之前输入了 \(3\) 条起始顶点不是 \(1\) 的边。那么这条边就应该存在 \(e_{3+3}\) 也就是 \(e_6\)。通向 \(3\),权值 \(6\),而它的上一条同一起始顶点的边在 \(e_3\),所以
nxt为 \(3\)。
最后,起始顶点为 \(1\) 的遍历过程就是:
- 先取 \(head_1\),发现最后一条边在 \(e_6\),先对 \(e_6\) 进行操作。
- 通过 \(e_6\) 的
nxt得知,另一条相同起始顶点的边在 \(e_3\),对 \(e_3\) 操作。 - 通过 \(e_3\) 的
nxt,对 \(e_2\) 进行操作。 - 通过 \(e_2\) 的
nxt,对 \(e_1\) 进行操作。
也不难理解吧?
下面是遍历某个顶点 \(u\) 的代码:
// 设 u 是要遍历的顶点
// 从第一条边开始遍历,每次找下一条边
// 要是遍历到最后一条边了,那么这条边的 nxt 一定为 0,退出循环
for(int i=head[u]; i; i=e[i].nxt){
int v=e[i].to,w=e[i].val;
// v 是 u 连向的一个顶点,w 是边权。
// do something
}
请注意,循环的第二项,也就是循环成立条件,为 \(i\) 是否等于 \(0\),因为 nxt 初值为 \(0\),如果还有相邻顶点,这个 nxt 一定指向某个节点在链表 \(e\) 中的下标。
\(i=0\) 时就说明没有相邻顶点了,退出。
如果最小顶点 \(\leq 0\) 怎么办呢?这就要先将 \(e\) 中所有 \(nxt\) 初始化为一个比最小顶点编号还要小的值,判断条件改为是否等于这个值,就可以顺利遍历了。
就是这么简单,链式前向星是目前最省空间的存图方式,有人说这个就是邻接表,虽说没什么大问题,但链式前向星还是与邻接表有区别的。
链式前向星这名字真帅...
图的遍历
图的遍历分为深度优先搜索和广度优先搜索,简单来说,就是搜索。
搜索对于图论来说,就是基础算法,很多图论算法都是基于搜索的。
深度优先搜索 (dfs)
一搜直接搜到底,然后回溯,再搜其它边。
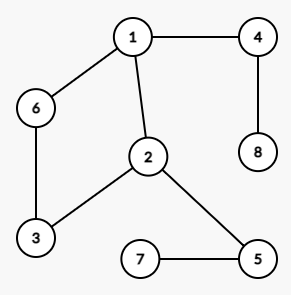
以这张图为例,让我们来看看它的深度优先搜索是如何进行的。
设搜索初始顶点为 \(1\)。
括号中代表搜索的顺序。一直搜到底才回溯,就是深度优先搜索。
这样就能成功遍历这张图了。那么这张图的深度优先搜索序(其中一种)就是:\(1,2,3,6,5,7,4,8\),深度优先搜索序可以有多种,取决于。代码也很好写,我们使用链式前向星存图,下面是 dfs 代码(输出搜索序):
// id表示搜索到的当前顶点
// vis数组表示是否访问过,初始值为0
// write是快读函数,输出后接一个空格
void dfs(int id){
vis[id]=1; // 标记
printf("%d\n",id) // 先输出
// 遍历顶点
for(int i=head[id]; i; i=e[i].nxt)
// 只要一个相邻顶点没访问过,就进去搜。
if(!vis[e[i].to])
dfs(e[i].to);
}
普遍的深度优先搜索序就是这样的,和树的前序遍历一样,如果需要求图的后序遍历,只需将输出语句放在函数末尾即可。
广度优先搜索 (bfs)
和树的广度优先搜索一样,可以将它想成同学传话,同学 \(1\) 号同时传给周围的几个同学,周围的几个同学又传给自己周围的同学,然后再传 \(\dots \dots\) 直到没有同学不知道要传的话了为止。
同样:

这次则是直接从左依次推到右,但你好像要学会分身术,是这样的(层次遍历关系):
- 顶点 \(1\)。
- 顶点 \(1\) 中:顶点 \(2\) 和 顶点 \(4\)。
- 顶点 \(2\) 中:顶点 \(3\),顶点 \(5\);顶点 \(4\) 中:顶点 \(8\)。
- 顶点 \(3\) 中:顶点 \(6\);顶点 \(5\) 中:顶点 \(7\)。
这样就可以生成广度优先搜索序了:\(\color{red}1\color{black},\color{orange}2\color{black},\color{orange}4\color{black},\color{gold}3\color{black},\color{gold}5\color{black},\color{gold}8\color{black},\color{green}6\color{black},\color{green}7\) 其中标了颜色,不同的颜色代表不同的层次。
至于代码,使用一个队列,每次将遍历的顶点的所有相邻顶点 push 进去,每次遍历使用队列头顶点,pop 掉,代码也很好写:
// vis数组表示是否访问过,初始值为0
// write是快读函数,输出后接一个空格
// q是队列
void bfs(){
q.push(1); // 初始顶点先入队
vis[1]=1; // 标记
while(!q.empty()){
int u=q.front();
q.pop();
write(u); // 先输出
for(int i=head[u]; i; i=e[i].nxt){
int v=e[i].to;
if(!vis[v]){ // 没去过才push
q.push(v); // 将每个相邻顶点扔进队列
vis[v]=1;
}
}
}
}
链式前向星存图是反着遍历的,它越早输入的边就越靠后遍历(数组的前面),head 指向的是最后一条连接某个顶点的边,依次找到第一条连接某个顶点的边,所以不是输入的顺序。
上面代码输入:
8 8
1 2
1 4
1 6
2 3
2 5
3 6
4 8
5 7
会输出一种广度优先搜索序:\(\color{red}1\color{black},\color{orange}6\color{black},\color{orange}4\color{black},\color{orange}2\color{black},\color{gold}8\color{black},\color{gold}5\color{black},\color{gold}3\color{black},\color{green}7\),这种顺序也是可以的。
P5318 【深基18.例3】查找文献
题目大意:
输入一张有向无权图,输出最小的 dfs 序和 bfs 序。
思路
既然让我们输出最小的序,那么邻接矩阵是无需做任何操作即可实现,但数据范围太大:\(n \leq 10^5\),邻接矩阵存不下,那就要考虑邻接表了,我们可以输入后先排序,再搜索。链式前向星也不合适,虽然更快,但做到排序还是很难的。
dfs 和 bfs 参考上面的链式前向星搜索,只需改变遍历方式即可。
代码
#include <iostream>
#include <cstring>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
template<typename T=int>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
template<typename T=int>
inline void write(T X){
if(X<0) putchar('-'),X=~(X-1);
T s[20],top=0;
while(X) s[++top]=X%10,X/=10;
if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
putchar(' ');
}
const int N=1e5+5;
int n,m,u,v;
bool vis[N];
queue<int> q; // 用来广搜的队列
vector<int> p[N]; // 邻接表
void dfs(int x){ // 和上面一样,深搜板子
vis[x]=1;
write(x);
// 就是遍历改了一下,邻接表
for(int i=0,len=p[x].size(); i<len; i++)
if(!vis[p[x][i]])
dfs(p[x][i]);
}
void bfs(){ // 也是一样的,就改遍历
q.push(1);
vis[1]=1;
while(!q.empty()){
u=q.front(); // u 可以直接用全局里定义的
q.pop();
write(u);
for(int i=0,len=p[u].size(); i<len; i++){
v=p[u][i]; // 同上的 u
if(!vis[v]){
q.push(v);
vis[v]=1;
}
}
}
}
int main(){
n=read(),m=read();
for(int i=1; i<=m; i++){
u=read(),v=read();
p[u].push_back(v); // 邻接表存图
}
for(int i=1; i<=n; i++)
sort(p[i].begin(),p[i].end()); // 排序所有顶点
dfs(1);
puts("");
memset(vis,0,sizeof(vis));
bfs();
puts("");
return 0;
}
推荐习题
拓扑排序
拓扑排序是对有向无环图上的顶点进行排序,使每一条 \(u \rightarrow v\) 边,\(u\) 总在 \(v\) 之前出现。就是将一个有向无环图拉成一条链,使顶点先后顺序不变。
我们称有向无环图为 DAG(Directed Acyclic Graph)。
想象一个场景:学习算法。
例如要学习拓扑排序,那要先学会什么是图,图的存储,图的遍历等知识。我们将每个算法抽象为一个顶点,入边是需要先学习的算法指来的,出边则是该算法学习后才可以学的算法。
可以证明,它是有向无环的。设想一下,如果有 \(3\) 个算法,分别为 \(1,2,3\),如果想学习 \(1\) 则需要先学习 \(3\),而学习 \(2\) 需要学习 \(1\),学习 \(3\) 需要学习 \(2\),那么就形成了一个环,无论怎么学都学不会任何一个算法。
拓扑排序一般就指使用 Kahn 算法,下面是具体流程:
- 将所有入度为 \(0\) 的顶点 push 进队列。
- 遍历队头 \(u\) 顶点的所有相邻顶点。
- 对于每一个点 \(v\),进行操作,并使其入度减一,删边。
- 当 \(v\) 入度为 \(0\) 时,push 进队列
- 重复第 \(2\) 条,直到队列为空为止。
其中的入度表示指向某个顶点的边的个数,入度为 \(0\) 即表示某个算法不需要先学习任何算法就能学会。
出度表示通过某个顶点指向其它顶点的边的个数,即为前置知识为这个算法的算法的个数。
P4017 最大食物链计数
题目大意
给出一张 DAG,求从入度为 \(0\) 的顶点到出度为 \(0\) 的顶点的路径总数 \(\bmod 80112002\)。
思路
拓扑排序板子题,用一个数组 \(f\) 表示从一个不会捕食其他生物的生产者到各个顶点的路径数,详细见代码。
代码
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
template<typename T=int>
inline T read(){
T X=0; bool flag=1; char ch=getchar();
while(ch<'0' || ch>'9'){if(ch=='-') flag=0; ch=getchar();}
while(ch>='0' && ch<='9') X=(X<<1)+(X<<3)+ch-'0',ch=getchar();
if(flag) return X;
return ~(X-1);
}
template<typename T=int>
inline void write(T X){
if(X<0) putchar('-'),X=~(X-1);
T s[20],top=0;
while(X) s[++top]=X%10,X/=10;
if(!top) s[++top]=0;
while(top) putchar(s[top--]+'0');
putchar('\n');
}
const int N=5e3+5,M=5e5+5,mod=80112002;
struct edge{
int to,nxt;
}e[M]; // 链式前向星
int n,m,u,v,ans;
int head[N],top;
int ind[N],outd[N],f[N]; // 入度,出度,从一个不会捕食其他生物的生产者到每个顶点的路径数
queue<int> q; // 拓扑排序用队列
void add(int u,int v){
top++;
e[top].to=v;
e[top].nxt=head[u];
head[u]=top;
outd[u]++; // 记录出度与入度
ind[v]++;
}
void topo(){
for(int i=1; i<=n; i++)
if(!ind[i]){
q.push(i); // push 入度为 0 的顶点
f[i]=1; // 有 1 条路径
}
while(!q.empty()){
int u=q.front();
q.pop();
for(int i=head[u]; i; i=e[i].nxt){
int v=e[i].to;
// 既然 u 能到 v,那么 v 的路径数就要加上 u 的路径数
f[v]=(f[u]+f[v])%mod; // 记得取模
if(!--ind[v]) // 删边并 push
q.push(v);
}
}
}
int main(){
n=read(),m=read();
for(int i=1; i<=m; i++){
u=read(),v=read();
add(u,v);
}
topo(); // 拓扑排序
for(int i=1; i<=n; i++)
if(!outd[i]) // 不会被任何生物捕食的消费者,也就是出度为 0,说明要计入答案
ans=(ans+f[i])%mod;
// 拓扑排序时已经记录了 f[i],f[i] 表示从一个不会捕食其它生物的生产者到当前生物的路径数
// 注意取模
write(ans);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号