『学习笔记』最小生成树(todo)

Kruskal

对边排序，依次加边，用并查集记录连通块，直到连为一棵树。\(O(m\log m)\)。

int kruskal(int n,int m){
    sort(e+1,e+m+1);
    set s;
    int ans=0,cnt=1;
    for(int i=1; i<=m; i++)
        if(s.find(e[i].u)!=s.find(e[i].v)){
            ans+=e[i].w;
            s.merge(e[i].u,e[i].v);
            if(++cnt==n)
                break;
        }
    if(cnt!=n) ans=-1145141919;
    return ans;
}

Prim

选取一个起点作为已选点，并选取与已选点最近的一个未选点并将其加入已选点。加入 \(n\) 个点后即为所求。加上堆优化，\(O(n\log n)\)。

int prim(){
    memset(dist,0x3f,sizeof(dist));
    dist[1]=0;
    q.push({0,1});
    int ans=0,cnt=0;
    while(!q.empty()){
        u=q.top().second,w=-q.top().first;
        q.pop();
        if(vis[u]) continue;
        vis[u]=1;
        ans+=w;
        if(++cnt==n) break;
        for(int i=head[u]; i; i=e[i].nxt){
            v=e[i].to;
            if(dist[v]>e[i].val){
                dist[v]=e[i].val;
                q.push({-dist[v],v});
            }
        }
    }
    if(cnt!=n) ans=-1145141919;
    return ans;
}

Boruvka

Kruskal + Prim = Boruvka（？）

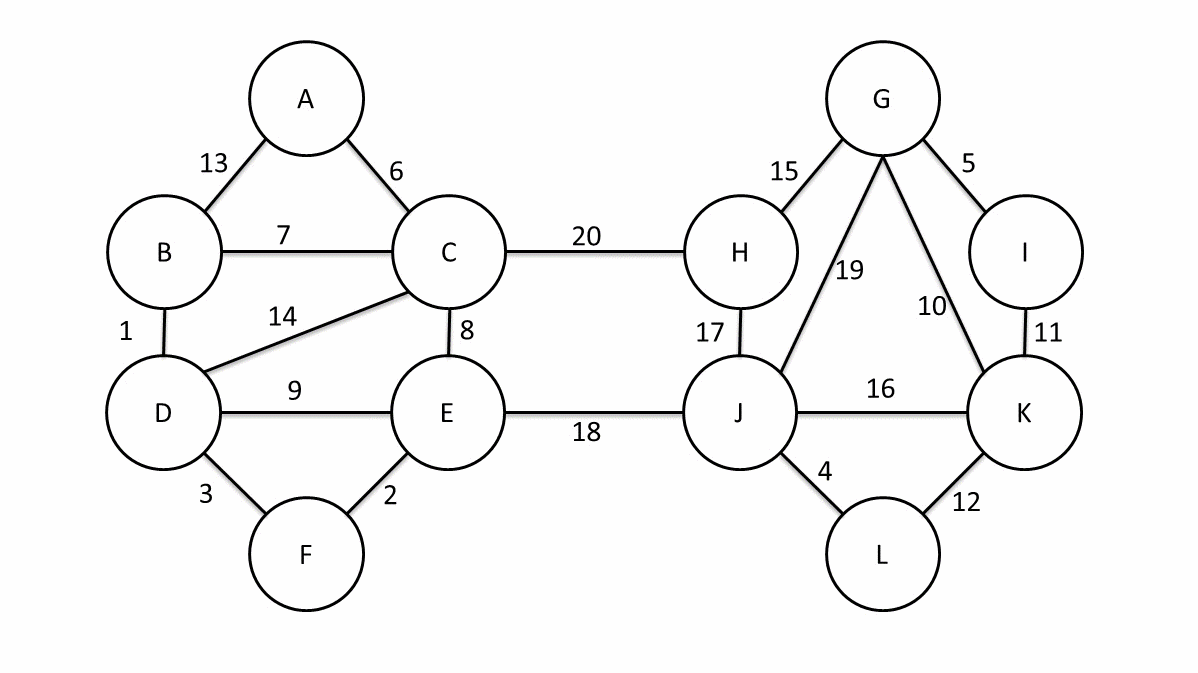
维护最小生成森林，每次选取每个连通块最小的连向其它连通块的边，合并两个连通块。具体如图。

每次合并至少会将连通块数量减半，故总复杂度 \(O(m\log n)\)。

inline bool cmp(int x,int y){
    return y==0 ? 1 : w[x]!=w[y] ? w[x]<w[y] : x<y;
}

void Boruvka(){
    s.clear(); // 并查集
    int cnt=n,sum=0,flg=1;
    while(flg){
        flg=0;
        memset(mn,0,sizeof(mn));
        for(int i=1; i<=m; i++){
            if(used[i]) continue;
            int a=s.find(u[i]),b=s.find(v[i]);
            if(a==b) continue;
            if(cmp(i,mn[a])) mn[a]=i;
            if(cmp(i,mn[b])) mn[b]=i;
        }
        for(int i=1; i<=n; i++)
            if(mn[i] && !used[mn[i]]){
                flg=1;
                used[mn[i]]=1;
                cnt--,sum+=w[mn[i]];
                s.merge(u[mn[i]],v[mn[i]]);
            }
    }
}