P4388 付公主的矩形

Luogu 链接

题意

题目描述

求有多少组无序整数对 \((R,C)\)，使得以 \(R\) 和 \(C\) 为长和宽作一个矩形（该矩形由 \(R\times C\) 个单位正方形组成），并连接该矩形的一条对角线，恰好穿过 \(n\) 个单位正方形。

---

输入格式

第一行一个正整数 \(n\)（\(1\le n\le10^6\)），含意见题目描述。

---

输出格式

见题目描述。

思路

我们先计算当 \(\gcd(R,C)=1\) 时，其穿过了多少正方形。

以下为图解：

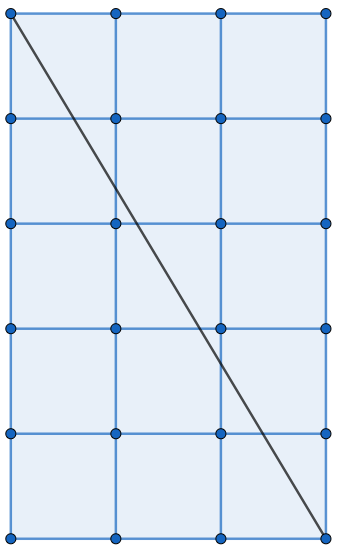
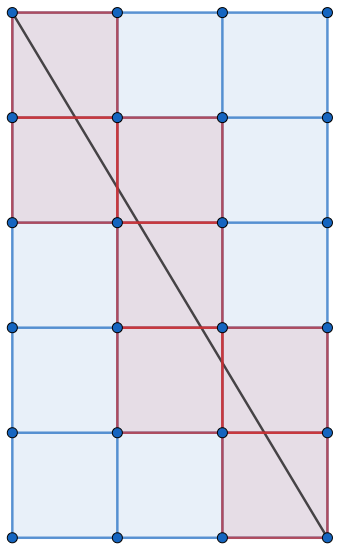
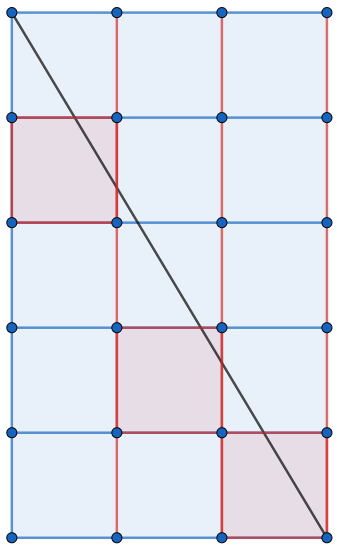
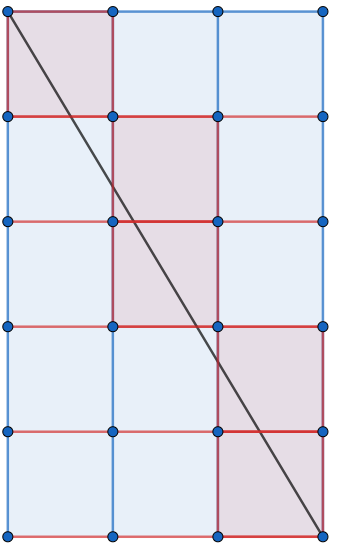
显然，对角线与每条红线有且只有一个交点，而每个交点都能唯一确定一个正方形（图中红色的正方形），再减去右下角被重复计算的一个正方形，可以得到对角线穿过了 \(R+C-1\) 个正方形。

而我们很容易就能推广至 \(\gcd(R,C)\neq 1\) 的情况。此时对角线穿过了 \(R+C-\gcd(R,C)\) 个正方形（因为有 \(\gcd(R,C)\) 个正方形会被重复计算）。

因此，问题就变为求满足 \(R+C-\gcd(R,C)=n\) 的无序整数对 \((R,C)\) 的数量。

不妨令 \(R'=\dfrac{R}{\gcd(R,C)},C'=\dfrac{C}{\gcd(R,C)},n'=\dfrac{n}{\gcd(R,C)}\)，可得 \(R'+C'=n'+1\)。

而 \(\gcd(R',C')=\gcd(R',n'+1-R')=\gcd(R',n+1)=1\)，因此当 \(\gcd(R,C)\) 确定时（不考虑无序的条件），其方案数为 \(\varphi(n'+1)\)。

因此，总方案数 \(\displaystyle ans=\sum_{n'\mid n}\varphi(n'+1)\)。

但是题目要求的是无序，所以真正的答案是 \(\dfrac{ans+1}{2}\)（\((n,n)\) 只会被计算一次，因此要先加 \(1\) 再除以 \(2\)）。

既可以用线性筛，也可以直接计算欧拉函数，这里采用线性筛的方法。

程序

AC 记录

#include<cstdlib>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<cstdio>
#include<iostream>
#include<vector>
#include<map>
#include<cmath>
#include<iomanip>
#include<string>
#include<stack>
#define ll long long
#define ull unsigned long long
#define INF 0x3f3f3f3f
#define ls rt<<1
#define rs rt<<1|1
#define lb(x) ((x)&(-(x)))
#define pb push_back
using namespace std;
const int N=1e6+10;
//#define use_file
//#define more_test
//#define need_init
#ifdef more_test
int T;
#endif

int n;

int cnt,p[N],phi[N];bool np[N];
void init(int n){
	phi[1]=1;
	for(int i=2;i<=n;++i){
		if(!np[i])p[++cnt]=i,phi[i]=i-1;
		for(int j=1;j<=cnt&&i*p[j]<=n;++j){
			np[i*p[j]]=true;
			if(i%p[j]==0){
				phi[i*p[j]]=phi[i]*p[j];
				break;
			}
			phi[i*p[j]]=phi[i]*phi[p[j]];
		}
	}
}

int ans;

void SOLVE(/*int test_id*/){
	scanf("%d",&n);
	init(n+1);
	for(int i=1;i<=n;++i)if(n%i==0)ans+=phi[i+1];
	printf("%d",(ans+1)>>1);
}
int main(){
	#ifdef use_file
	freopen("test.in","r",stdin);
	freopen("test.out","w",stdout);
	#endif
	#ifdef need_init
	init();
	#endif
	#ifdef more_test
	scanf("%d",&T);
	for(int i=1;i<=T;++i)SOLVE(/*i*/);
	#else
	SOLVE();
	#endif
	return 0;
}