CF1059D Nature Reserve

Luogu 链接
CodeForces 链接
Virtual Judge 链接

题意

题目描述

在坐标系中有 \(n\) 个点，其中第 \(i\) 个点的坐标为 \((x_i,y_i)\)。

求包含这 \(n\) 个点，且与 \(x\) 轴相切的圆的最小半径 \(r\)（与答案误差不超过 \(10^{-6}\) 即可，若无解则输出 \(-1\)）。

---

输入格式

第一行一个整数 \(n\)（\(1\le n\le 10^5\)），含义见题目描述。
后面 \(n\) 行每行两个实数 \(x_i\ y_i\)（\(-10^7\le x_i,y_i\le 10^7,y_i\neq0\)），含义见题目描述。

---

输出格式

见题目描述。

思路

首先，由于这个圆与 \(x\) 轴相切，所以它所包含的点一定是全在 \(x\) 轴上方或全在 \(x\) 轴下方。

因此我们可以先遍历这 \(n\) 个点，用两个布尔变量记录是否有在 \(x\) 轴上方或在 \(x\) 轴下方的点。若两个变量同时为真，则输出 \(-1\)。

如果 \(n\) 个点全在 \(x\) 轴下方，我们可以将它们关于 \(x\) 轴做个轴对称，转移到 \(x\) 轴上方，这样就只需要处理在 \(x\) 轴上方的情形。

然后我们可以对 \(r\) 进行二分答案，此时圆心的 \(y\) 坐标我们就知道了（\(y=r\)），但 \(x\) 坐标仍然不知道，该怎么办呢？

其实并没有关系，我们可以对于每个点都计算下当圆包含它时，圆心的 \(x\) 坐标的取值范围，然后判断这 \(n\) 个区间是否有交集即可。若有，则该 \(r\) 可行，否则不可行。

例如，对于第 \(3\) 组样例，模拟情况如下：

• \(r=1\)
  

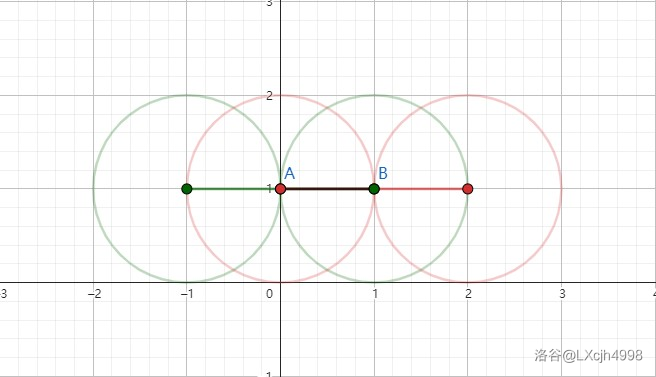
圆心 \(x\) 坐标的取值范围为 \([0,1]\)。

• \(r=0.5\)
  

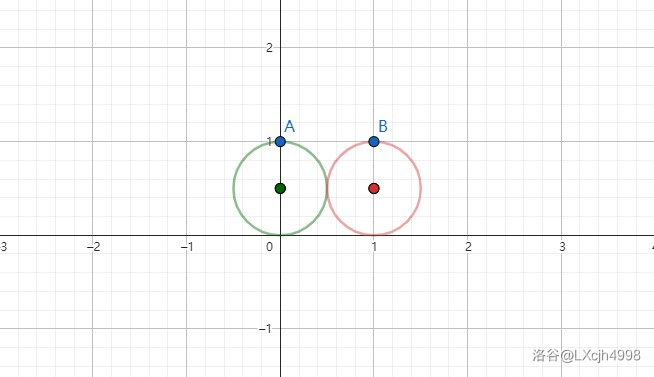
圆心 \(x\) 坐标的取值范围为空集。

• \(r=0.75\)
  

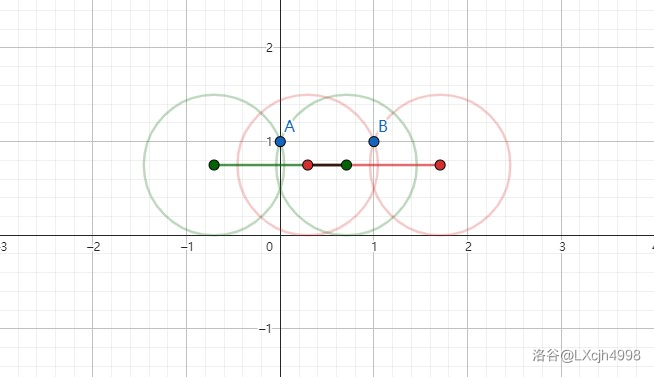
圆心 \(x\) 坐标的取值范围为 \([1-\frac{\sqrt 2}{2},\frac{\sqrt 2}{2}]\)，约为 \([0.293,0.707]\)。

• \(r=0.625\)
  

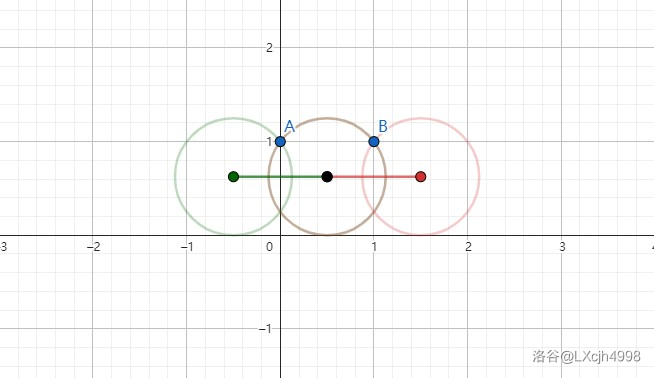
圆心 \(x\) 坐标的取值范围为 \(\{0.625\}\)。

因此输出结果为：

0.625

程序

AC 记录

#include<cstdlib>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#include<cstdio>
#include<iostream>
#include<vector>
#include<map>
#include<cmath>
#include<iomanip>
#include<stack>
using namespace std;
int T=1;
#define ll long long
#define ull unsigned long long
#define LL 2e18
#define INT 1e9
#define INF 0x3f3f3f3f
#define mod int(1)
#define MAX int(1e5)
//#define DEBUG
//#define use_cin
//#define more_text

struct point{//x为点的横坐标，y为点的纵坐标 
	double x,y;
};
int n;point arr[MAX];//n为点的个数，arr[]存点的坐标 
double l,r,mid,ans;//用于二分答案 
bool flag1,flag2;//用于判断点与x轴的相对位置（在上方还是在下方）

bool check(double num){//检查函数 ，num为圆的半径 
	double le=-1e18,ri=1e18;//le记录当前区间左端点的最大值，ri记录当前区间右端点的最小值 
	double dis;
	
	for(int i=0;i<n;++i){
		if(2*num<arr[i].y)return false;//如果圆中y坐标最大的点仍低于该点，则返回false 
		dis=sqrt((2*num-arr[i].y)*arr[i].y);//计算区间端点到圆心的距离 
		le=max(le,arr[i].x-dis);//左端点 
		ri=min(ri,arr[i].x+dis);//右端点 
	}
	
	return le<ri;//返回 
}
void solve(int step){
	scanf("%d",&n);//输入 
	for(int i=0;i<n;++i)scanf("%lf%lf",&arr[i].x,&arr[i].y);
	
	flag1=flag2=false;//判断点与x轴的相对位置 
	for(int i=0;i<n;++i){
		if(arr[i].y>0)flag1=true;
		if(arr[i].y<0)flag2=true;
	}
	if(flag1&&flag2){//若存在两个点分居x轴的两侧，则输出-1 
		printf("-1");
		return;
	}
	
	if(flag2)for(int i=0;i<n;++i)arr[i].y=-arr[i].y;//如果在x轴下方，则改为在x轴上方 
	
	l=0,r=1e14+10;//二分答案 
	int t=1000;
	while(t--){
		mid=(l+r)/2;
		if(check(mid))ans=mid,r=mid;
		else l=mid;
	}
	
	printf("%.6lf",ans);//输出 
}
int main(){//模板，不用在意
	#ifdef DEBUG
	freopen("test.in","r",stdin);freopen("test.out","w",stdout);
	#endif
	#ifdef more_text
	#ifdef use_cin
	cin>>T;
	#else
	scanf("%d",&T);
	#endif
	#endif
	for(int i=0;i<T;++i)solve(i);
	#ifdef DEBUG
	fclose(stdin);fclose(stdout);
	#endif
	return 0;
}
/*
Input:

*/