题解:qoj7872 崩坏天际线
没看懂官方题解,手搓了一个笛卡尔树做法,参考了 nullptr_qwq 的题解和陈昕阳的代码。
题意:有两种操作:
- 给出一个区间 \([l,r]\)。
- 给出一个 \(x\),对于所有满足 \(l<x<r\) 的区间 \([l,r]\),各有 \(\frac{1}{2}\) 的概率变成 \([l,x],[x,r]\)。
求最后所有区间的长度之和的期望值。\(l<r\le n,n,q\le 5\times 10^4\)。
做法:
首先先观察对于一个区间怎么做,因为一个区间只会被切 \(O(q)\) 次,所以直接对切分点按时间为小根笛卡尔树,在笛卡尔树上从上往下,记录当前区间被切成了什么样,然后每被切一次就要乘上 \(\frac{1}{2}\) 的概率,直接做,暴力重构笛卡尔树可以做到 \(O(q^2)\)。
然后注意到 sub3 有一个非常好的性质:所有区间都在分裂前给出。这个就非常好做了,因为我们发现我们只需要建立一次笛卡尔树了,重点在于如何优化计算。
举个例子,假设我们有区间 \([3,9]\),构造出来的笛卡尔树是这样的:
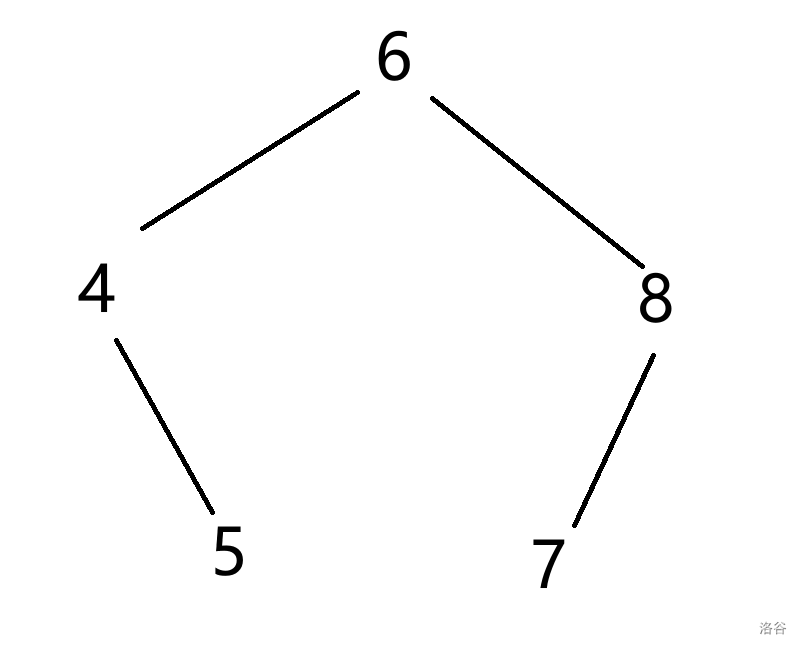
最后会出来 \([3,4],[4,5],[5,6],[6,7], [7,8],[8,9]\)。
我们发现切分出来的区间只有两端是散的,中间的都是整段。
可以比较类似 ioi 会议那一题处理,就变成线段树上区间乘法加法之类的一系列维护。
但是还有第二种做法,发掘性质,假设我们对于区间 \([l,r]\) 找到 \(l\) 后第一个切分和 \(r\) 前第一个切分 \([lx,rx]\),那么后面的其实是固定的。对于他们 lca 左侧的 \(lx\),向上这一条链中 \(lx\) 和所有下一步是走左儿子的点 \(u\),右儿子整棵子树的概率都要加上 \(\frac 1 {2^{\text{u 向上经过了多少次向左边+1}}}\) 的概率,类似 \(rx\) 也有如此贡献。发现这个东西可以树上差分维护。
然后对于全部的做法,直接对上面这个东西两种做法做一个询问分块。块内暴力拆分,用 \(O(q^2)\) 的做法,块外就等于我这个操作区间里的区间都给出了,我只用管后面拆分点对这些区间的影响。复杂度 \(\frac{q^2}B\log q+B^3\)。可以做到 \(O(q\sqrt{q\log q})\)。
然而这个题还有更优的做法。注意到我们前面这些东西都建立在一个错误的结论上:对于一个操作序列,分裂出来的区间是 \(O(q^2)\) 的。实际本质不同的区间是 \(O(q)\) 的!因为对于一个区间 \([l,r]\) 来说,他只会被切分点切出来最左最有两个散块,而中间的都是重复多次的整块,贡献为 \(O(1)\),而对于每个切分点来说,他只会新增左右两种整块,也是 \(O(1)\),合起来总共的区间其实只有 \(O(q)\) 个。
所以我们直接对操作序列上 cdq 分治,对于左侧区间直接跑出来有哪些区间,然后考虑右侧区间的划分点去跑上面 sub3 的第二种方法,再用多一次 dfs 把区间全部取出来。再把右区间的区间跑出来,合并并去重。感觉结合代码会更容易理解一点。
复杂度 \(O(q\log^2 q)\)。
代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 5e4 + 5, mod = 998244353, inv2 = (mod + 1) / 2;
int n, q, op[maxn], l[maxn], r[maxn], pw[maxn];
struct Seg {
int l, r, w;
inline friend bool operator<(Seg x, Seg y) {
return (x.l != y.l ? x.l < y.l : x.r < y.r);
}
};
int val[2][maxn], s[maxn], lf[maxn], rf[maxn], dep[2][maxn];
int son[maxn][2], st[maxn], top, depth[maxn], a[maxn], f[maxn];
// lf 左侧第一个切分点,rf 右侧;跟 0 相关都是右子树,跟 1 相关都是左子树
// val 是树上差分的 tag
inline void clr() {
top = 0;
}
inline void clear(int p) {
son[p][0] = son[p][1] = 0; lf[p] = rf[p] = 0;
val[0][p] = val[1][p] = s[p] = dep[0][p] = dep[1][p] = 0;
f[p] = 0; depth[p] = 0;
}
inline void ins(int p) {
int pre = 0;
clear(p);
while(top && a[st[top]] > a[p])
pre = st[top--];
son[p][0] = pre;
if(top)
son[st[top]][1] = p;
st[++top] = p;
}
int stt[21][maxn << 1], dfn[maxn], tot;
inline int get_max(int x, int y) {
return (depth[x] < depth[y] ? x : y);
}
int lg[maxn << 1];
inline void prepare() {
lg[0] = -1;
for (int i = 1; i <= tot; i++)
lg[i] = lg[i >> 1] + 1;
for (int j = 1; (1 << j) <= tot; j++)
for (int i = 1; i + (1 << j) - 1 <= tot; i++)
stt[j][i] = get_max(stt[j - 1][i], stt[j - 1][i + (1 << j - 1)]);
}
inline int lca(int x, int y) {
x = dfn[x], y = dfn[y];
if(x > y)
swap(x, y);
int k = lg[y - x + 1];
return get_max(stt[k][x], stt[k][y - (1 << k) + 1]);
}
void dfs1(int u) {
dfn[u] = ++tot; stt[0][tot] = u;
if(son[u][0]) {
rf[son[u][0]] = f[son[u][0]] = u; lf[son[u][0]] = lf[u];
dep[0][son[u][0]] = dep[0][u] + 1; dep[1][son[u][0]] = dep[1][u];
depth[son[u][0]] = depth[u] + 1;
dfs1(son[u][0]);
stt[0][++tot] = u;
}
if(son[u][1]) {
lf[son[u][1]] = f[son[u][1]] = u; rf[son[u][1]] = rf[u];
dep[0][son[u][1]] = dep[0][u]; dep[1][son[u][1]] = dep[1][u] + 1;
depth[son[u][1]] = depth[u] + 1;
dfs1(son[u][1]);
stt[0][++tot] = u;
}
}
void dfs2(int u) {
if(son[u][0])
dfs2(son[u][0]);
if(son[u][1])
dfs2(son[u][1]);
val[0][rf[u]] = (val[0][rf[u]] + val[0][u] * 2) % mod;
val[1][lf[u]] = (val[1][lf[u]] + val[1][u] * 2) % mod;
// 每向上一层都少一个 1/2,乘上 2
}
vector<Seg> tp;
void dfs3(int u) {
// cout << u << " asdf" << s[u] << " " << val[0][u] << " " << val[1][u] << " " << lf[u] << " " << rf[u] << endl;
if(son[u][0]) {
s[son[u][0]] = (s[son[u][0]] + inv2 * (s[u] + val[1][u])) % mod;
dfs3(son[u][0]);
// 有左儿子,需要加上左子的贡献一起下传
}
else
tp.push_back(Seg{lf[u], u, inv2 * (s[u] + val[1][u]) % mod});
// 无左子,和 lf 构成一个区间,只加上左侧的贡献
if(son[u][1]) {
s[son[u][1]] = (s[son[u][1]] + inv2 * (s[u] + val[0][u])) % mod;
dfs3(son[u][1]);
}
else
tp.push_back(Seg{u, rf[u], inv2 * (s[u] + val[0][u]) % mod});
// 右子对应讨论
}
vector<int> pos;
int rt;
void build(int lx, int rx) {
// cout << lx << " asdfsdf" << rx << endl;
clr(); pos.clear();
for (int i = lx; i <= rx; i++) {
if(op[i] == 2) {
if(!a[l[i]]) {
a[l[i]] = i;
pos.push_back(l[i]);
}
}
}
sort(pos.begin(), pos.end());
for (int i = 0; i < pos.size(); i++)
ins(pos[i]);
for (int i = 1; i < top; i++)
son[st[i]][1] = st[i + 1];
rt = st[1]; tot = 0;
lf[rt] = 0, rf[rt] = n + 1;
dfs1(rt);
prepare();
for (int i = 0; i < pos.size(); i++)
a[pos[i]] = 0;
}
void solve(vector<Seg> &vec) {
tp.clear();
// cout << val[0][4] << " " << val[1][4] << endl;
// for (int i = 0; i < pos.size(); i++)
// cout << pos[i] << " asdf";
// cout << rt << endl;
// cout << endl;
for (int i = 0; i < vec.size(); i++) {
int l = vec[i].l, r = vec[i].r, w = vec[i].w;
int lx = upper_bound(pos.begin(), pos.end(), l) - pos.begin();
int rx = lower_bound(pos.begin(), pos.end(), r) - pos.begin() - 1;
if(lx > rx) {
tp.push_back(vec[i]);
continue;
}
lx = pos[lx], rx = pos[rx];
int d = lca(lx, rx);
// cout << l << " " << r << " " << lx << " " << rx << " " << d << " " << w << endl;
val[0][lx] = (val[0][lx] + w * pw[dep[0][lx] - dep[0][d]]) % mod;
val[1][rx] = (val[1][rx] + w * pw[dep[1][rx] - dep[1][d]]) % mod;
val[0][d] = (val[0][d] - w + mod) % mod;
val[1][d] = (val[1][d] - w + mod) % mod;
tp.push_back(Seg{l, lx, w * pw[dep[0][lx] - dep[0][d] + 1] % mod});
tp.push_back(Seg{rx, r, w * pw[dep[1][rx] - dep[1][d] + 1] % mod});
}
// cout << val[0][4] << " " << val[1][4] << endl;
dfs2(rt);
dfs3(rt);
}
void mrg(vector<Seg> &x, vector<Seg> &y) {
for (int i = 0; i < y.size(); i++)
x.push_back(y[i]);
}
vector<Seg> solve(int lx, int rx) {
if(lx == rx) {
vector<Seg> ans;
if(op[lx] == 1)
ans.push_back(Seg{l[lx], r[lx], 1});
return ans;
}
int mid = lx + rx >> 1;
vector<Seg> lans = solve(lx, mid);
build(mid + 1, rx);
if(pos.size())
solve(lans), lans = tp;
vector<Seg> rans = solve(mid + 1, rx);
mrg(lans, rans);
sort(lans.begin(), lans.end());
vector<Seg> ans;
for (int l = 0, r; l < lans.size(); l = r + 1) {
r = l;
while(r < lans.size() && lans[l].l == lans[r].l && lans[l].r == lans[r].r)
r++;
r--;
int res = 0;
for (int i = l; i <= r; i++)
res = (res + lans[i].w) % mod;
if(lans[l].l < lans[l].r && res)
ans.push_back(Seg{lans[l].l, lans[l].r, res});
}
// cout << lx << " " << rx << endl;
// for (int i = 0; i < ans.size(); i++)
// cout << ans[i].l << " " << ans[i].r << " " << ans[i].w << endl;
return ans;
}
signed main() {
cin >> n >> q;
for (int i = 1; i <= q; i++) {
cin >> op[i];
if(op[i] == 1)
cin >> l[i] >> r[i];
else
cin >> l[i];
}
pw[0] = 1;
for (int i = 1; i <= n; i++)
pw[i] = pw[i - 1] * inv2 % mod;
vector<Seg> res = solve(1, q);
int ans = 0;
for (int i = 0; i < res.size(); i++)
ans = (ans + (res[i].r - res[i].l) * res[i].w) % mod;
cout << ans << endl;
return 0;
}
/*
100 6
1 1 100
2 25
1 5 9
2 12
2 4
2 8
*/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号