题解：qoj7979 棋盘

为数不多自己能乱搞出来的构造题。

题意：现有一个平面，在 \((1,1)\) 处有一个棋子。棋盘上有若干处被标记，\((1,1)\) 处必须被标记，记 \(f_{i,j}\) 为棋子到达 \((i,j)\) 且只能经过被标记的点的方案数。

现在要求你给出一种标记方式，同时给出 \(Q\) 次询问，每次询问从你标记的点中选若干个出来，满足这些点的 \(f\) 之和等于询问的 \(x\)。

范围：标记的点数 \(X\le 960\)，选出的点数 \(Y\le240\)，询问次数 \(Q\le 10^4\)，询问的 \(x \le 10^{100}\)。

做法：

首先手玩几下，可以很容易先搓出来一个二进制的构造：

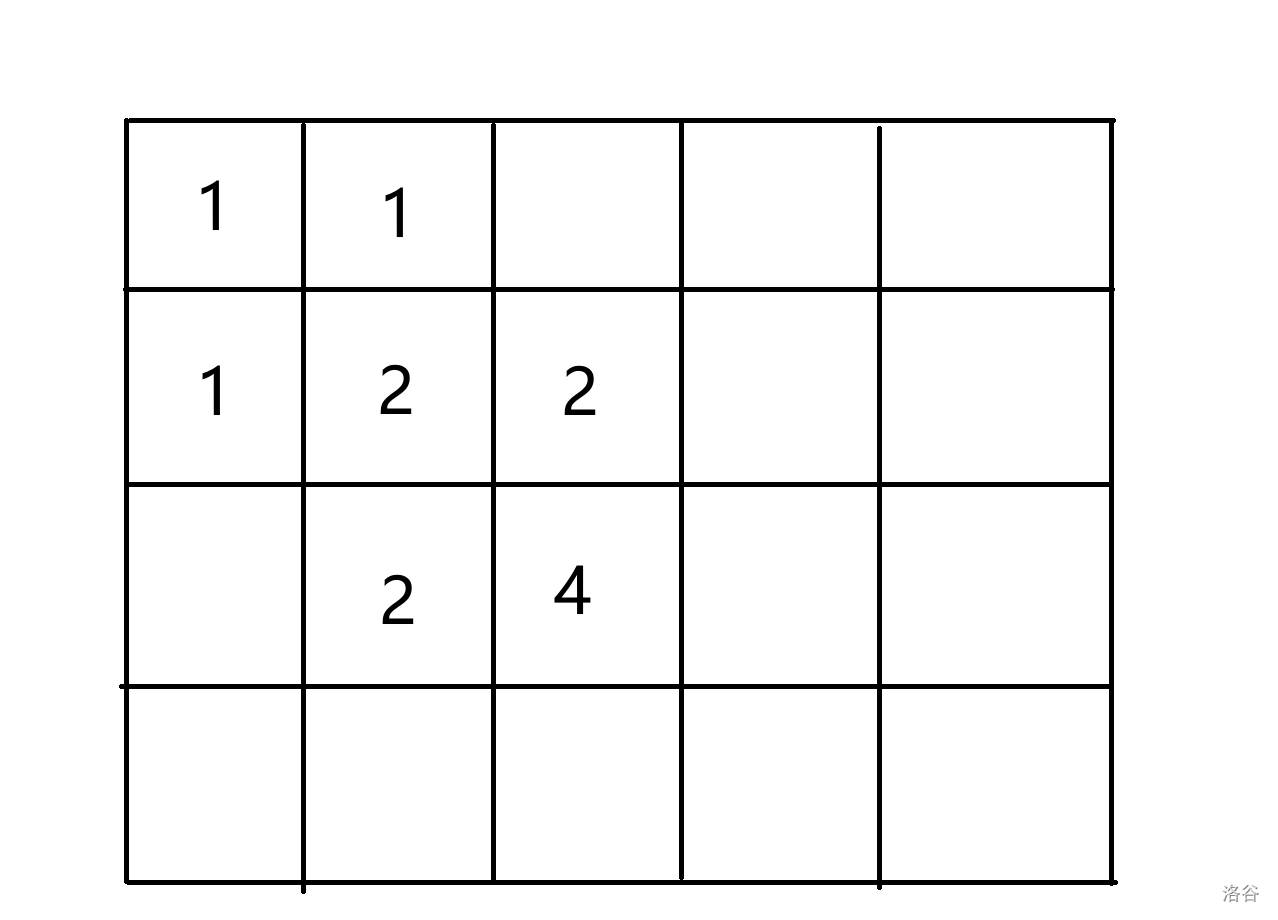
这样我们可以以 \(3\) 的代价使我的数乘 \(2\)，可以做到 \(X=3\log_2{10^{100}} \approx 996\)，但是这时候 \(Y = \log_{2}{10^{100}} \approx 332\)。可以过前三个 sub。

然后既然有二进制那么就有三进制等等，但是尝试之后发现 \(Y\) 都比较大压不进去，所以我们考虑其他东西，比如斐波那契数。

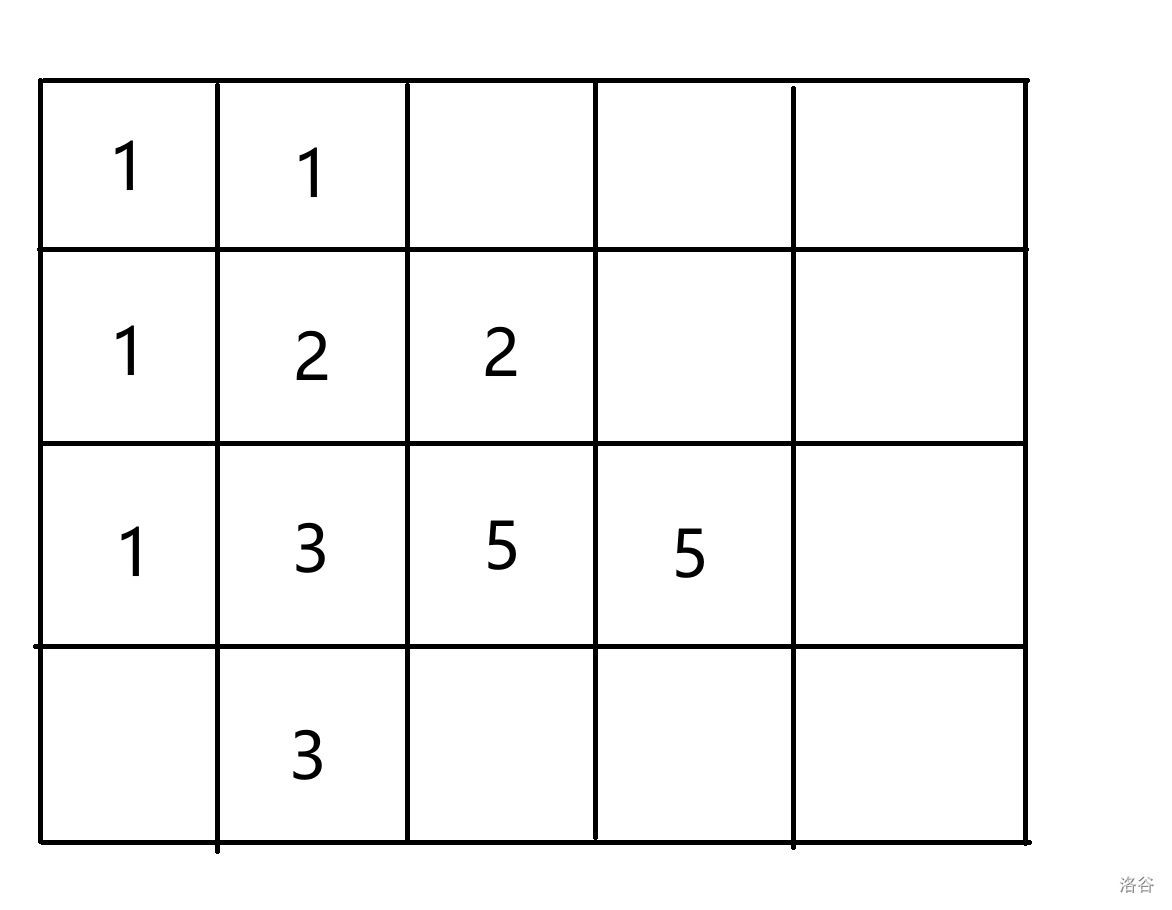
两个两个这样交错构造。

因为 \(f_n\) 是 \(O(\phi^n)\) 级别的，这里 \(\phi = \frac{1+\sqrt 5}{2}\)，所以我们可以做到 \(X=2\log_{\phi}10^{100} < 960\)，然后因为每个数都有唯一的斐波那契分解，且相邻两个都不会同时取，所以 \(Y<240\)。按上述构造即可。

代码：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1005;
struct Big_int {
	vector<int> a;
	Big_int() {
		
	}
	Big_int(int x) {
		while(x) {
			a.push_back(x % 10);
			x /= 10;
		}
	}
	Big_int(string s) {
		reverse(s.begin(), s.end());
		for (int i = 0; i < s.size(); i++)
			a.push_back(s[i] - '0');
	}
	void resize(int N) {
		a.resize(N);
	}
	void pop_back() {
		a.pop_back();
	}
	void push_back(int x) {
		a.push_back(x);
	}
	int& operator[](int x) {
		return a[x];
	}
	int size() {
		return a.size();
	}
	friend Big_int operator+(Big_int x, Big_int y) {
		int d = max(x.size(), y.size());
		x.resize(d), y.resize(d);
		for (int i = 0; i < d; i++)
			x[i] = x[i] + y[i];
		for (int i = 0; i < d - 1; i++)
			x[i + 1] += x[i] / 10, x[i] %= 10;
		while(x[d - 1] >= 10) {
			x.push_back(x[d - 1] / 10);
			x[d - 1] %= 10, d++;
		}
		return x;
	}
	friend Big_int operator-(Big_int x, Big_int y) {
		int d = max(x.size(), y.size());
		x.resize(d), y.resize(d);
		for (int i = 0; i < d; i++) {
			if(x[i] < y[i])
				x[i] += 10, x[i + 1] -= 1;
			x[i] -= y[i];
		}
		while(x.size() && x[x.size() - 1] == 0)
			x.pop_back();
		return x;
	}
	friend bool operator<=(Big_int x, Big_int y) {
		if(x.size() != y.size())
			return x.size() < y.size();
		for (int i = x.size() - 1; i >= 0; i--)
			if(x[i] != y[i])
				return x[i] < y[i];
		return 1;
	}
	void print() {
		for (int i = a.size() - 1; i >= 0; i--)
			cout << a[i];
		cout << endl;
	}
} f[maxn];
int k, q, x, y;
struct node {
	int x, y;
} ;
int id[maxn];
int vis[maxn];
int main() {
	cin >> k >> q >> x >> y;
	f[1] = 1, f[2] = 1; 
	for (int i = 3; i <= 480; i++)
		f[i] = f[i - 1] + f[i - 2];
	vector<node> v;
	for (int i = 1; i <= 480; i++) {
		if(i % 2)
			v.push_back(node{i / 2 + 1, i / 2 + 1}), v.push_back(node{i / 2 + 1, i / 2 + 2}), id[i] = v.size() - 1;
		else
			v.push_back(node{i / 2 + 1, i / 2}), v.push_back(node{i / 2 + 2, i / 2}), id[i] = v.size() - 1;
	}
	cout << v.size() << endl;
	for (int i = 0; i < v.size(); i++)
		cout << v[i].x << " " << v[i].y << endl;
	while(q--) {
		string s;
		cin >> s;
		Big_int x(s);
		memset(vis, 0, sizeof(vis));
		for (int i = 480; i >= 1; i--) {
			if(f[i] <= x)
				x = x - f[i], vis[id[i]] = 1;
		}
		x = Big_int(0);
		for (int i = 1; i <= 960; i++) {
			cout << vis[i];
			if(vis[i])
				x = x + f[(i + 1) / 2];
		}
		cout << endl;
	//	x.print();
	}
	return 0;
}