题解：AT_arc184_d [ARC184D] Erase Balls 2D

题意：很简单了，不再赘述。

做法：

计数最后剩下的太麻烦，很简单的想法是记录哪些删掉了。但是感觉也不是很靠谱，因为经常来说，直接计算删掉了的那些，可能会有很多种删掉的方式最后导出了同样的结果。

先声明一种删除方案：选一个序列 \(p_1,p_2,\cdots p_k\)，删掉 \(X\) 值为这些的点。

一般来说，我们考虑对这样的东西加一些限制使得删掉的和保留的一一对应，我们先考虑随意画出来一种删除方案，考虑什么样的删除方案会和他一样。

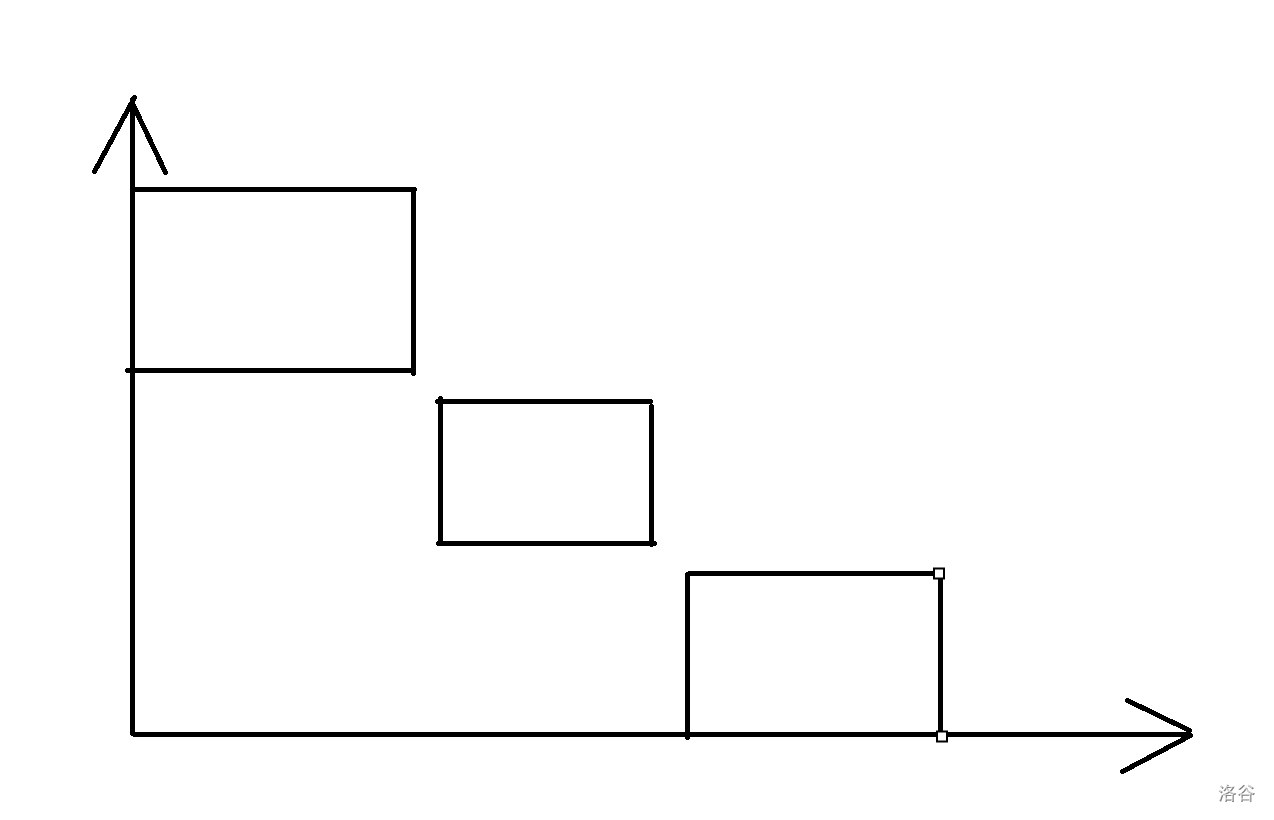
两个矩形之间有一个点删除，这里不是很方便画出来，保留的就是方格中的点。

那么考虑，如果说这些方格里存在一个点，满足对他进行操作之后仍然不变，那么完全可以再多选上他。所以我们这么加限制：对于没被选入删点集合且没有被删掉的点，他们如果被选入删点集合，那么会有更多的点被删掉。

考虑有了这个怎么计算，直接枚举最后一个选入删点集合的为 \(i\)，然后枚举上一个点 \(j\)，暴力扫 \([j+1,i-1]\) 的点是否满足条件即可，为了方便，我加入了 \((0,n+1),(n+1,0)\) 这两个点。

代码：

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 305, mod = 998244353;
int n, p[maxn], dp[maxn], use[maxn];
signed main() {
	cin >> n;
	p[0] = n + 1;
	for (int i = 1; i <= n; i++) {
		int x, y; cin >> x >> y;
		p[x] = y;
	}
	dp[0] = 1;
	for (int i = 1; i <= n + 1; i++) {
		for (int j = 0; j < i; j++) {
			if(p[j] < p[i])
				continue;
			int mn = p[j];
			for (int k = j + 1; k < i; k++)
				use[k] = 0;
			for (int k = j + 1; k < i; k++) {
				if(p[k] < p[i] || p[k] > p[j])
					continue;
				if(mn < p[k])
					use[k] = 1;
				else
					mn = p[k];
			}
			mn = p[i];
			bool f = 1;
			for (int k = i - 1; k >= j + 1; k--) {
				if(p[k] < p[i] || p[k] > p[j])
					continue;
				if(mn > p[k])
					use[k] = 1;
				else
					mn = p[k];
				f &= use[k];
			}
			dp[i] = (dp[i] + dp[j] * f) % mod;
		}
	}
	cout << dp[n + 1] << endl;
	return 0;
}