题解：AT_agc032_f [AGC032F] One Third

超级牛牛题。

题意：很简单了，不再赘述。

做法：

首先要知道一些经典结论。

在 \([0,1)\) 上随机撒 \(n-1\) 个点，那么最小的那一段长度期望为 \(\frac{1}{n^2}\)。

证明：

首先转化：

\[E(x) = \int_{0}^1 P(l_{min}\ge x)dx \]

然后考虑 \(P(l_{min}\ge x)\)，这个东西我们可以先给所有的区间长度减去 \(x\)，那么就等于剩下 \((1-nx)\) 里面随机撒 \(n-1\) 个点，那么有：

\[E(x)=\int_{0}^1 (1-nx)^{n-1}dx \]

\[E(x) = -\frac1 n\int_{0}^{\frac1 n}(1-nx)^{n-1}d(1-nx) \]

\[E(x) = \frac{1}{n^2} \]

我们证明了这个结论。

进一步的，我们去拓展这个结论。

对于第 \(k\) 小的段，期望长度为 \(\frac 1 n\sum\limits_{i=1}^k\frac{1}{n-i+1}\)。

这个就直接在前面结论的基础上，直接推就可以了。

---

有了上面这个结论之后我们还是不会做，这个 \(|\frac 1 3 - x|\) 状物的东西太难算了。

考虑一个神仙转化，我们考虑以第一刀为起点，每面积 \(\frac 1 3\) 的部分划分为一个区域，并且把其中的每一刀染上区域的颜色，并且红色结束的位置为红色，绿色结束的位置为绿色，蓝色结束的位置为蓝色。

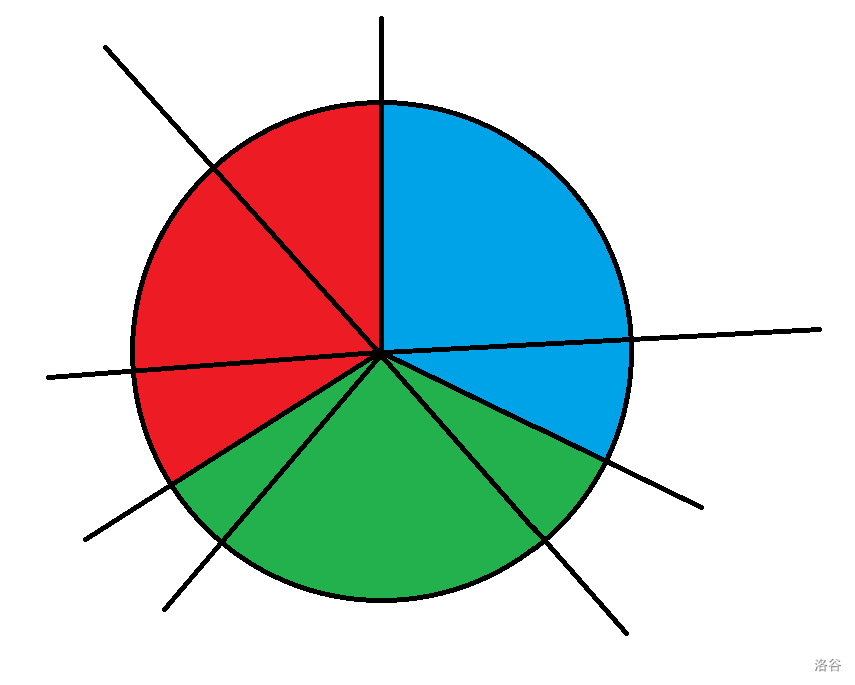
然后我们把这些线全部转到同一部分中，转的量是若干个 \(\frac 2 3\pi\)，这里转到绿色的这里，同时标出绿色这一块临界的两条线的颜色。

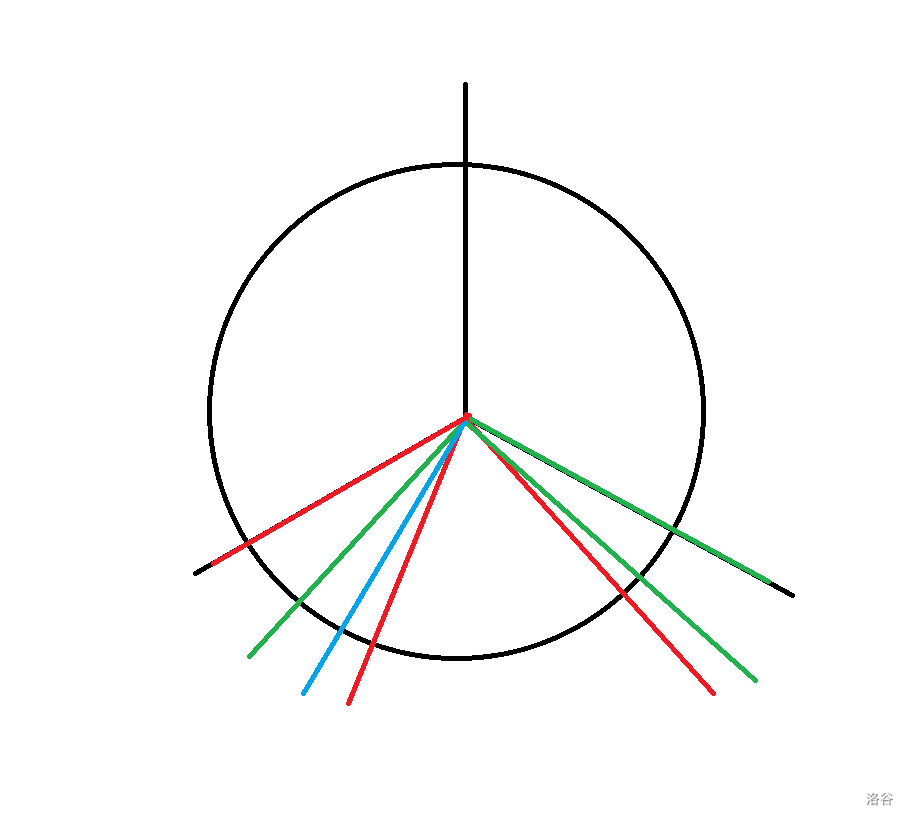
那么我们可以说明我们的答案就是相邻的异色直线所切分出来的最小距离。

我们直接讨论一下：

1. 两个原本是异色的直线：稍微分讨一下，对于在红色和蓝色两部分的切分，经过这么转化完把原本的距离 \(x\) 转化为了 \(|1-x - \frac{2}{3}|\)，刚好是 \(|x-\frac{1}{3}|\)，而对于有一侧在绿色部分中的，这个转量刚好帮我们把 \(\frac 1 3\) 减掉了。

2. 两个原本是同色的直线：稍微分讨一下，会发现应有的贡献其实不如异色的。

但是这里有个问题，比如我有两个同色的直线他们夹角特别小，这样虽然他实际的代价很大，但是会影响我们计算最小的异色段。

所以我们考虑枚举是第 \(x\) 小的段，那么对于前 \(x - 1\) 个段颜色相同的概率是 \(\frac{1}{3^{x-1}}\)，减去第 \(x\) 个段颜色相同的概率 \(\frac{1}{3^x}\)，注意 \(x=n\) 的时候，因为我限定了两端的颜色是不同的，所以这里是不可能存在 \(n\) 个段都是一个颜色的。

那么答案就是 \(\frac 1 3\sum\limits_{i=1}^nE(l_n)(\frac{1}{3^{i-1}}-\frac 1{3^i}[i\not = n])\)。

这个柿子直接按上面展开化简就是 \(\frac 1 n\sum\limits_{i=1}^n\frac{1}{3^i(n-i+1)}\)。