题解：AT_agc035_e [AGC035E] Develop

题意：很简单了，不再赘述。

做法：

首先我们进行一步转化，我们考虑令 \(x\) 向 \(x-2,x+k\) 连边，那么对于一个删除的点集，显然不能成环，否则删不完，并且对于一个无环的点集我们直接按照拓扑序删除显然是可以的，然后转化为我们如何求有多少个点集是可以被删除的。

首先我们先对 \(k\) 的奇偶性分讨。

1. \(k\) 是偶数。

那么我们将点按奇偶性拉开，每一部分都会长成下面这样，这里以奇数为例，\(k=4,n=8\)。

那么我们直接从前往后 dp，就行 \(dp_{i,j}\) 代表前 \(i\) 个点，连续选了 \(j\) 个的答案，要求 \(j<\frac{k}2 +1\)。最后算答案的时候把奇数和偶数的答案乘在一起就行。

2. \(k\) 是奇数。

以 \(n=8, k=3\) 为例：

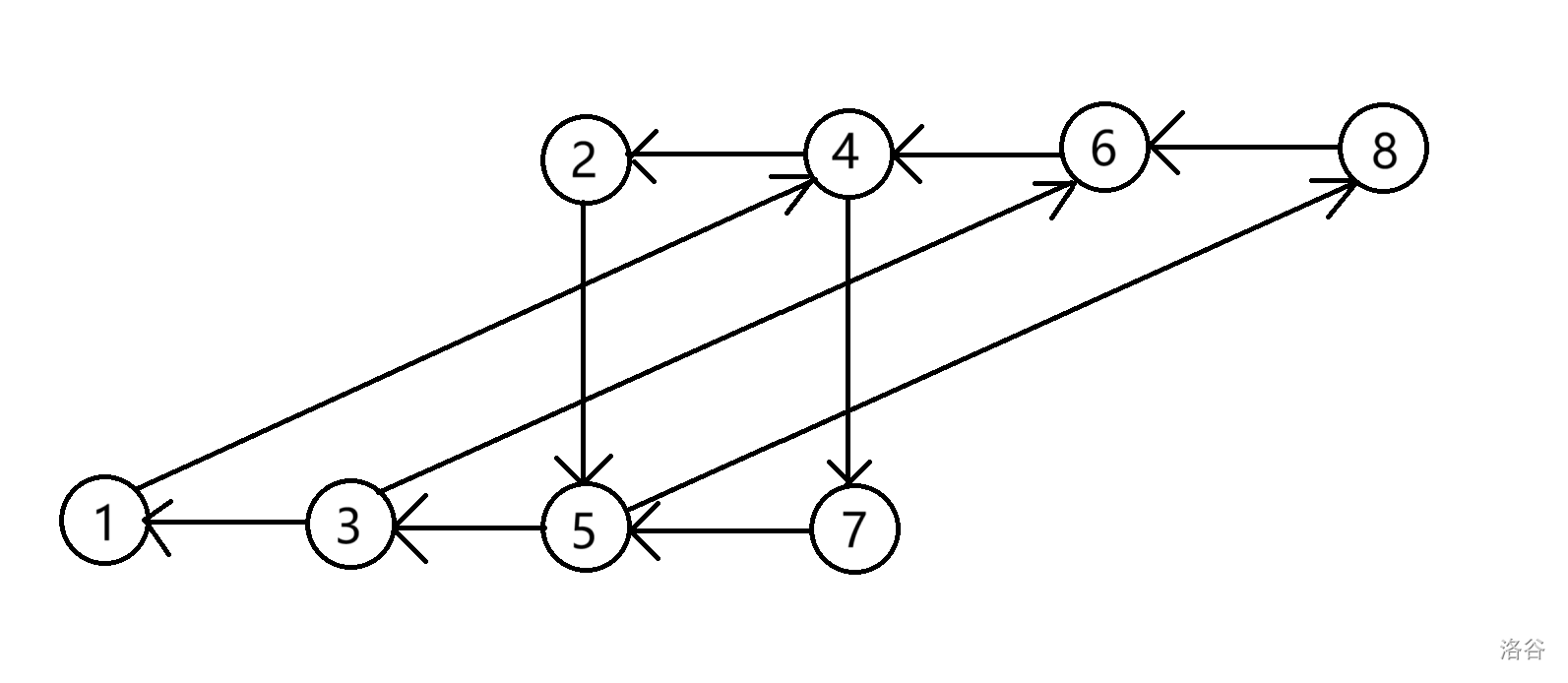
在这个图上的环长是 \(k+2\)，知道这个我们就能比较方便地去判定我们是否有一个环。

发现这个图显然是一个分层的形式，我们考虑从左到右，一层一层地 dp，显然是有 \(\frac{n+k}2\) 层的。

考虑这么 dp，\(dp_{i,p,q}\) 代表我们现在考虑到了从左到右第 \(i\) 层，其中从第二行开始且不到第一行的链最长为 \(p\)，从第一行开始并且必须往下走到第二行的最长的链长为 \(q\)。注意到我们根本没有提到奇数到偶数的这一条 \(+k\) 边怎么使用，因为如果我们的 \(q\) 达到 \(k+2\)，那么我们就可以用这条边回来，否则其实是没用的，所以这样的边我们只是作为一个限制，要求 \(q\le k+1\) 即可，注意我们没有对 \(p\) 限制。

那么考虑怎么转移，我们考虑枚举第一行第二行的点选或不选，注意到有些地方对位是没有的，比如第二列中其实是没有第一行的点的，这种我们直接认为是不选。

第一行不选，第二行不选：这种情况很简单，我们的 \(p,q\) 往后是没法扩展一点，所以有：

\[dp_{i,0,0} = \sum_{p=0}^n\sum_{q=0}^{k+1}dp_{i-1,p,q} \]

第一行选，第二行不选：那么对于第二行肯定就没法扩展了，\(p\) 变成了 \(0\)，但是对于 \(q\) 不能单纯的变成 \(q+1\)，原因是当 \(q=0\) 的时候，因为第二行没选，但是我们的状态定义里要求一定需要走到第二行，所以 \(q\) 还是 \(0\)，这个需要特殊判断，有转移式：

\[dp_{i,0,q+1} = \sum_{p=0}^n dp_{i-1,p,q}(q>0) \]

\[dp_{i,0,0} = \sum_{p=0}^n dp_{i-1, p, 0} \]

第一行不选，第二行选：那么 \(q=0\)，\(p\) 会加一，所以有：

\[dp_{i,p+1,0} = \sum_{q=0}^{k+1}dp_{i,p,q} \]

第一行选，第二行选：对于 \(p\) 很简单，直接加一，但是对于 \(q\) 有两种，第一种是我们接在 \(i-1\) 的链上，第二种是我们直接在第 \(i\) 行下去走第二行的链，最后形成的最长链要对两者取 \(\max\)，有转移式：

\[dp_{i,p+1,\max(p+2,q+1)} = \sum_{p=0}^n\sum_{q=0}^{k+1}dp_{i,p,q} \]

直接对着上面这一坨柿子转移即可，总复杂度 \(O(n^3)\)。