题解：P6976 [NEERC 2015] Distance on Triangulation

题意：给出一个三角剖分图，求图上任意两个点的最短路。

做法：

三角剖分图这样的图非常有性质，举个例子：

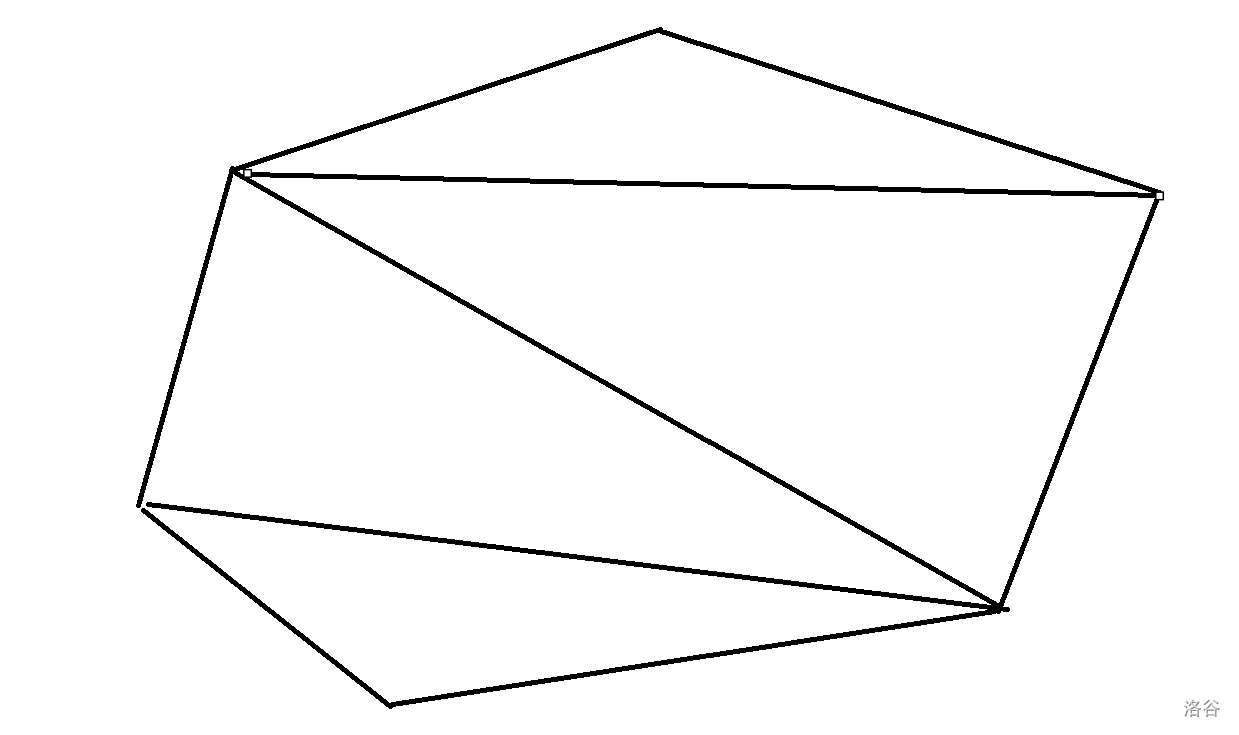
我们把每个三角形标号，按照有邻边来连接：

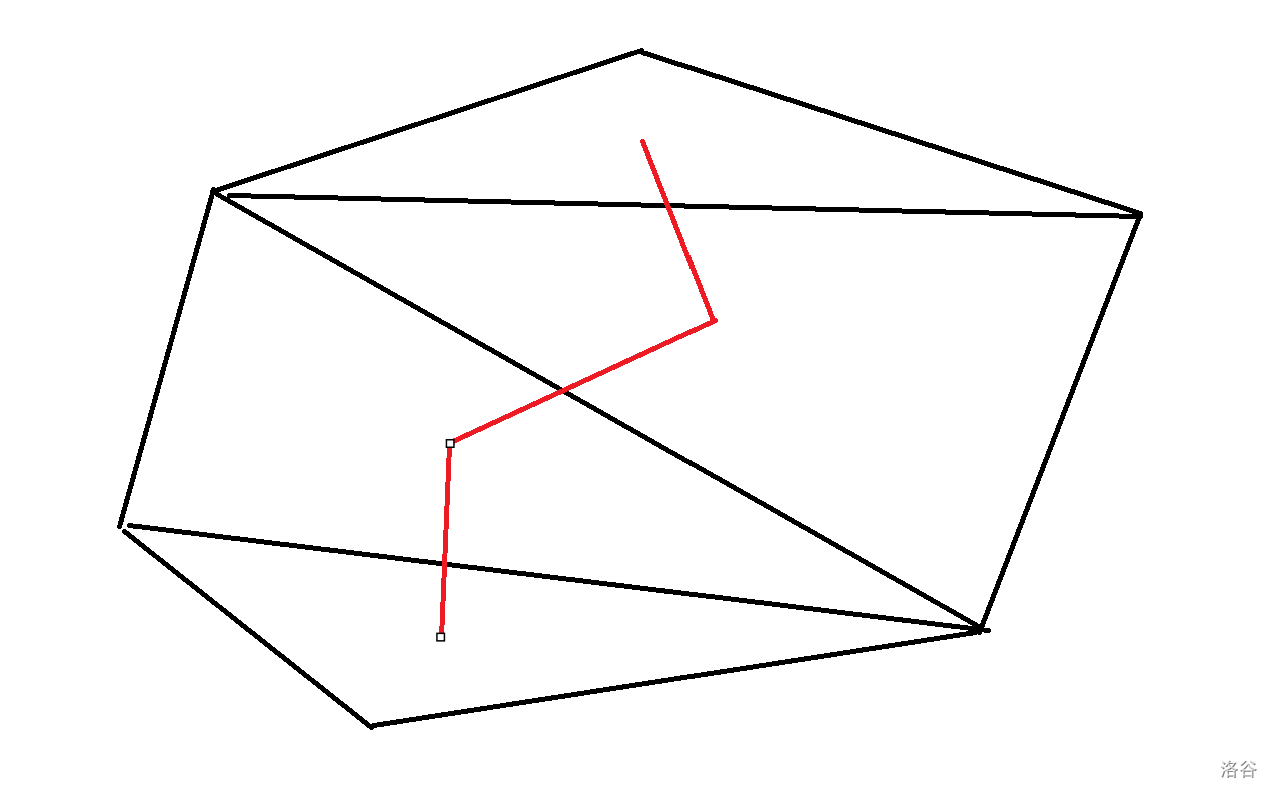
我们会发现这样我们会连出来一颗度数 \(\le 3\) 的树！那其实这样的话我们就可以考虑对这棵树边分治，一刀劈开这个多边形，类似猫树的想法去计算答案。

具体的，我们先特判答案为 \(0/1\) 的情况，然后因为这棵树上的边一定会跨过中间的一条中间的剖分的边，我们以这条边的两个端点跑 bfs，直接去回答当前分治时的询问集合，但是对于被这条边分在同一侧的询问其实还是有可能有更小的答案的，我们就把他往两边丢即可。

类似地比较多次询问两个点一棵树上的距离，我们考虑对于一个经过当前边的询问其实是不需要再去递归了，但是两侧的询问我们要往左右扔。

可能说的有点抽象，给出代码帮助理解一下：

#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
int n, deg[maxn], use[maxn], q;
vector<int> e[maxn];
struct Edge{
	int to, val;
};
vector<Edge> g[maxn];
map<pair<int, int>, int> mp, in;
map<pair<int, int>, pair<int, int> > cr;
struct tri {
	int x, y, z;
} t[maxn];
int sx[maxn], sy[maxn], ans[maxn];
vector<int> nw;
void add(int x, int y) {
//	cout << x << " " << y << endl;
	g[x].push_back(Edge{y, 0});
	g[y].push_back(Edge{x, 0});
}
void topo() {
	queue<int> q;
	for (int i = 1; i <= n; i++) {
		if(deg[i] == 2)
			q.push(i);
	//	cout << deg[i] << " ";
	}
//	cout << endl;
	for (int i = 1; i <= n - 2; i++) {
		int u = q.front(); q.pop();
		use[u] = 1;
		int a = 0, b = 0;
		for (int j = 0; j < e[u].size(); j++) {
			if(!use[e[u][j]]) 
				(!a ? a : b) = e[u][j];
		}
		t[i] = {u, a, b};
	//	cout << u << " " << a << " " << b << endl;
		if(mp[make_pair(u, a)])
			add(i, mp[make_pair(u, a)]), cr[make_pair(i, mp[make_pair(u, a)])] = cr[make_pair(mp[make_pair(u, a)], i)] = make_pair(u, a);
		if(mp[make_pair(u, b)])
			add(i, mp[make_pair(u, b)]), cr[make_pair(i, mp[make_pair(u, b)])] = cr[make_pair(mp[make_pair(u, b)], i)] = make_pair(u, b);
		if(mp[make_pair(a, b)])
			add(i, mp[make_pair(a, b)]), cr[make_pair(i, mp[make_pair(a, b)])] = cr[make_pair(mp[make_pair(a, b)], i)] = make_pair(a, b);
		else
			mp[make_pair(a, b)] = i, mp[make_pair(b, a)] = i;
		for (int j = 0; j < e[u].size(); j++) {
			deg[e[u][j]]--;
			if(deg[e[u][j]] == 2)
				q.push(e[u][j]);
		}
	}
	for (int i = 1; i <= n; i++)
		use[i] = 0;
}
int xt, yt, mx, sz[maxn], all;
void getsz(int u, int fa) {
	sz[u] = 1; all++;
	for (int i = 0; i < g[u].size(); i++) {
		Edge v = g[u][i];
		if(v.val || v.to == fa)
			continue;
		getsz(v.to, u);
		sz[u] += sz[v.to];
	}
}
void getrt(int u, int fa) {
	for (int i = 0; i < g[u].size(); i++) {
		Edge v = g[u][i];
		if(v.val || v.to == fa)	
			continue;
		if(max(sz[v.to], all - sz[v.to]) < mx)
			mx = max(sz[v.to], all - sz[v.to]), xt = u, yt = v.to;
		getrt(v.to, u);
	}
}
void clr(int x, int y) {
	for (int i = 0; i < g[x].size(); i++) 
		if(g[x][i].to == y)
			g[x][i].val = 1;
	for (int i = 0; i < g[y].size(); i++)
		if(g[y][i].to == x)
			g[y][i].val = 1;
}
vector<int> pos;
void renew(int u, int c) {
	use[t[u].x] = use[t[u].y] = use[t[u].z] = c;
	pos.push_back(t[u].x), pos.push_back(t[u].y), pos.push_back(t[u].z);
}
void get_col(int u, int fa, int c) {
	renew(u, c);
	for (int i = 0; i < g[u].size(); i++) {
		Edge v = g[u][i];
		if(v.to == fa || v.val)
			continue;
		get_col(v.to, u, c);
	}
}
int dis[maxn];
void bfs(int s) {
	for (int i = 0; i < pos.size(); i++) 
		dis[pos[i]] = -1;
	dis[s] = 0;
	queue<int> q;
	q.push(s);
	while(!q.empty()) {
		int u = q.front(); q.pop();
		for (int i = 0; i < e[u].size(); i++) {
			int v = e[u][i];
			if(dis[v] == -1 && use[v])
				q.push(v), dis[v] = dis[u] + 1;
		}
	}
}
void solve(int x, int y, vector<int> &nw, int d) {
	if(!nw.size())
		return ;
//	cout << x << " adsf" << y << " " << mx << endl;
	clr(x, y);
	get_col(x, y, 1), get_col(y, x, 2);
	int s1 = cr[make_pair(x, y)].first, s2 = cr[make_pair(x, y)].second;
//	cout << s1 << " " << s2 << endl;
	bfs(s1);
	for (int i = 0; i < nw.size(); i++) {
		ans[nw[i]] = min(ans[nw[i]], dis[sx[nw[i]]] + dis[sy[nw[i]]]);
//		if(nw[i] == 29)
//			cout << dis[sx[nw[i]]] << " " << sx[nw[i]] << " " << dis[sy[nw[i]]] << endl;
	}
	bfs(s2);
	for (int i = 0; i < nw.size(); i++)
		ans[nw[i]] = min(ans[nw[i]], dis[sx[nw[i]]] + dis[sy[nw[i]]]);
//	for (int i = 0; i < nw.size(); i++)
//		if(nw[i] == 29)
//			cout << sx[nw[i]] << " " << sy[nw[i]] << " " << ans[nw[i]] << " " << s1 << " " << s2 << endl;
	vector<int> nwl, nwr;
	for (int i = 0; i < nw.size(); i++) {
		if(use[sx[nw[i]]] == use[sy[nw[i]]])
			if(use[sx[nw[i]]] == 1)
				nwl.push_back(nw[i]);
			else
				nwr.push_back(nw[i]);
	}
	for (int i = 0; i < pos.size(); i++)
		use[pos[i]] = 0;
	pos.clear();
	
	all = 0, getsz(x, y), mx = 2e9, getrt(x, y);
	if(sz[x] != 1)
		solve(xt, yt, nwl, d + 1);
	all = 0, getsz(y, x), mx = 2e9, getrt(y, x);
	if(sz[y] != 1)
		solve(xt, yt, nwr, d + 1);
}
int main() {
	ios::sync_with_stdio(false);
	cin >> n;
	for (int i = 1; i <= n; i++) {
		deg[i] += 2;
		int x = (i == 1 ? n : i - 1), y = (i == n ? 1 : i + 1);
		e[i].push_back(x), e[i].push_back(y);
		in[make_pair(i, x)] = 1;
		in[make_pair(i, y)] = 1;
	}
	for (int i = 1; i <= n - 3; i++) {
		int x, y; cin >> x >> y;
		e[x].push_back(y);
		e[y].push_back(x);
		in[make_pair(x, y)] = 1;
		in[make_pair(y, x)] = 1;
		deg[x]++, deg[y]++;
	}
	topo();
	cin >> q;
	for (int i = 1; i <= q; i++) {
		cin >> sx[i] >> sy[i], ans[i] = 2e9;
		if(in[make_pair(sx[i], sy[i])] || sx[i] == sy[i])
			ans[i] = (sx[i] != sy[i]);
		else
			ans[i] = 2e9, nw.push_back(i);
	}
	all = 0, getsz(1, 0), mx = 2e9, getrt(1, 0);
	solve(xt, yt, nw, 0);
	for (int i = 1; i <= q; i++)
		cout << ans[i] << endl;
	return 0;
}