wqs 二分

wqs 二分可以优化一些 dp，最常见的是 ”选一些物品，次数有限制，使总价值最大“，有以下限制：

• 定义 \(g(k)\) 为恰好用 \(k\) 此操作能获得的最大收益，那么 \(g(k)\) 要满足上凸。

• 如果不考虑限制，可以比较快地求出答案。

前置

股票买卖Ⅰ

有 \(n\) 天，每天股票有一个价值 \(a_i\)，但是每次手里只能有一支股票，每买卖一次需要花 \(c\) 的手续费，求最大价值。

首先有个很明显的 dp 做法，\(dp_{i,0/1}\) 代表第 \(i\) 天时手里 没有/有 股票的最大价值，答案就是 \(dp_{n,0}\)。

但是还有一个反悔贪心的做法，我们先让第一天强制买入，然后对于当前，假设股票价值为 \(q\) 考虑以下操作：

1. 如果上次操作是 ”买入 \(p\) 价值的一个股票“：

如果 \(q < p\)，那么买贵了，我们改成 ”买入 \(q\)“。

如果 \(q > p + c\)，那么卖了可以赚钱，我们添加一个 ”卖出 \(q\)“。

2. 如果上次操作是 ”卖出 \(p\)“：

如果 \(q > p\)，那么卖便宜了，改成 ”卖出 \(q\)“。

如果 \(q < p - c\)，那么我们添加一个 ”买入 \(q\)“。因为如果 \(q \ge p - c\)，那么后面卖出一个 \(r\) 的时候，不如把 ”卖出 \(p\)“ 改成 ”卖出 \(r\)“，这样更优。

正题

股票买卖Ⅱ

有 \(n\) 天，每天股票有一个价值 \(a_i\)，但是每次手里只能有一支股票，只能进行 \(k\) 次交易，求最大价值。

首先很显然可以 dp 求解，复杂度 \(O(nk)\)。而使用 wqs 可以得到一个 log 的算法。

思考费用流，发现这个东西根据 SSP 的费用流增广办法，增广路价值肯定是单减的。

所以我们把 $g(k) = $ 恰好 \(k\) 次操作能得到的最大值 这个东西的图像画出来，大概是这样的：

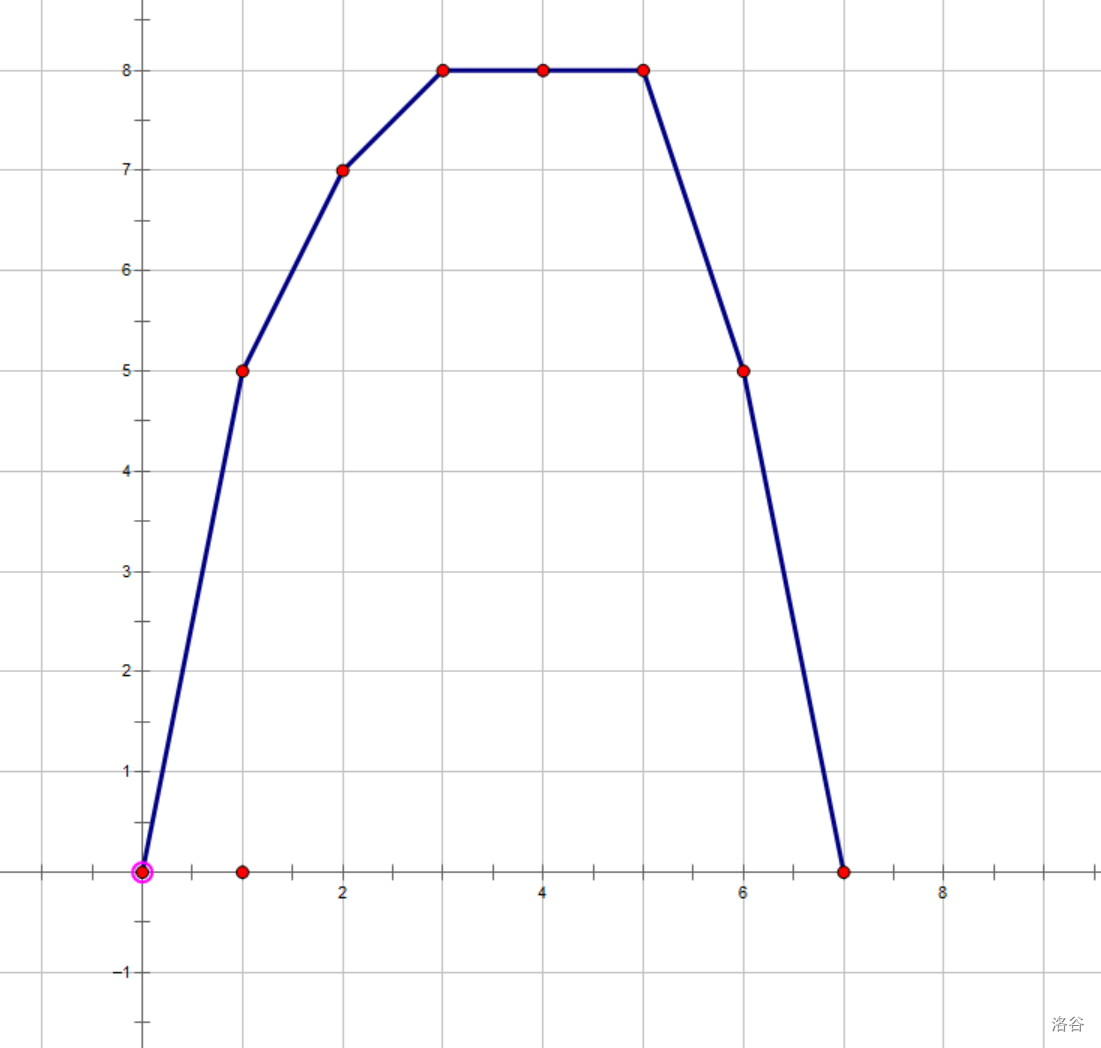
那么我们现在考虑随机选择一个价值 \(c\)，每次交易需要 \(c\) 的手续费。

那么假设我们有手续费时最优解为 \(ans\)，那么会有 \(ans + p\times c = g(p)\)，注意到这个函数是一个凸包，所以你可以认为有一个斜率为 \(c\) 的直线去切这个凸包，切出来的就是最大值，我们这个时候就可以无视交易次数的限制，就转化为 股票买卖Ⅰ。

然后我们可以二分斜率 \(c\)，就可以求出在 \(k\) 点切时最优的 \(ans\)，就可以反求 \(g(k)\) 了。

但是问题在于，我们现在可能有多点共线，那么我们就想要最小操作次数的那个位置，在解决 股票买卖Ⅰ 的时候，我们就要避免收入为 0 的买卖，这样就是最小的。

然后对于这个题，我们如果想要操作次数小于等于 \(k\) 的，那么我们可以把二分斜率的下界改成 \(0\)，这样就一定是最大的了。

注意在 wqs 二分中，经常出现多点共线的情况，要注意判断。

P4383 [八省联考 2018] 林克卡特树

首先可以转化成划分 \(k + 1\) 条端点互不相交的路径。

考虑一个费用流建图：

先把所有点拆成 \(u,u+n\)，一个入点一个出点，然后相邻边 \(u+n\rightarrow v,v+n\rightarrow u,u\rightarrow u+n\)，跑费用流就行，所以这个函数是上凸的。

考虑 wqs 二分，每次选出一个路径收费 \(c\)。

记 \(dp_{u,0/1/2}\) 代表 \(u\) 子树中，\(u\) 连了 0/1/2 条边的最大值。

初始值为 \(dp_{u, 0} = 0, dp_{u,1} = -\infty, dp_{u,2} = -c\)。

前两个好理解，最后一个是把他当成一个单点的路径，那就是连了一个自环，度数为 2。

那么当我们加入一个子树 \(v\) 的时候，记 \(val = w_{u,v}\)，有转移：

\[dp_{u,0} = dp_{u,0} + \max\{dp_{u,0},dp_{u,1},dp_{u,2}\} \]

这个比较显然。

\[dp_{u,1} = \max(\max(dp_{v,0} - c, dp_{v,1}) + val + dp_{u, 0}, \max\{dp_{v,0},dp_{v,1},dp_{v,2}\} + dp_{u,1}) \]

这个解释一下，前半部分是考虑这一条边连 \(v\)，那么如果 \(v\) 没有边，那么就等于我连出了一条新路径 \(u\rightarrow v\)，要多收 \(c\) 的费用，或者 \(v\) 有边。

而后半部分，就是考虑已经有边了，那么 \(v\) 可以随便选几条边。

\[dp_{u,2} = \max(\max(dp_{v,0} + val, dp_{v,1} + val + c) + dp_{u, 1}), dp_{u,2} + \max{dp_{v,0},dp_{v,1}, dp_{v,2}}) \]

前半部分是考虑连一条到 \(v\)，但是对于 \(v\) 已经有路径时，这么做相当于把两条路径合并为 1 条，要补回来 \(c\)，后半部分就是已经有两条的情况。

注意这个东西要先存一份再更新就好。

wqs 与费用流

如果一个题能建出费用流模型，那么他一定具有凸性，因为每次增广得到的路径肯定是越来越长的，所以就是凸的。