环计数

感悟于

简单环计数

• 简单环: 点不同，边不同的环
• 自然的，设 \(dp_{s,i}\) 点集为 \(s\)，最后选的点为 \(i\)，初始点为 \(s\) 中最小的方案数。
• 枚举下一个走到的点 \(u\) 若 \(u\) 为环起点，统计答案，否则需满足 \(u\) 不再 \(s\) 中，就转移.
• 最后总方案数，就等于 \(\frac{cnt-m}{2}\)，减 \(m\) 为减去重边，\(\div 2\) 是因为，一个环被正反统计两次

三元环计数

• 关键想法： 我们对所有点按照在原图的度数从小到大排序，若是两点度数相同，就取编号小的排在前面，\(u\) 的度数记作 \(d_u\)

• 然后我们构建新图，把无向边定向，排序后小的 指向 排序后大的

• 我们暴力枚举 \(u\) 点，之后暴力枚举 \(v\)，满足 \(u\to v\)，再之后枚举 \(w\) 满足 \(v\to w\)，然后只需要判断存不存在 \(u\to w\) 就行了

• 论证复杂度：

  • 若 \(d_u\le \sqrt{m}\)，枚举 \(v\) 花费 \(\sqrt{m}\) 次，枚举 \(w\) 花费 \(n\) 次，次部分总复杂度为 \(n\sqrt{m}\)
  • 若 \(d_u>\sqrt{m}\) ，枚举 \(d_w\ge d_v\ge d_u>\sqrt m\)，也就是说我们枚举 \(u\to v\) 从总体考虑最多也就 \(m\) 次，总共就 \(m\) 条边，有 \(2m\) 次度的贡献，\(d_w>\sqrt m\) 的点，包小于根号个，于是复杂度 \(O(m\sqrt m)\)
  • 所以其实根号具体怎么取最优也不重要，总之直接这样枚举复杂度就是对的

四元环计数

• 依旧像三元环计数一样构建新图。
• 考虑 \(burnside\) 引理，得出本质不同的四圆环排列方式有 \(3\) 种，正好复习一下（乐）
• 这里不是只考虑轮换，还考虑了翻转。
• \(ABCD,ABDC,ACBD\) 就是他们仨，是三个等价类选出的代表元素

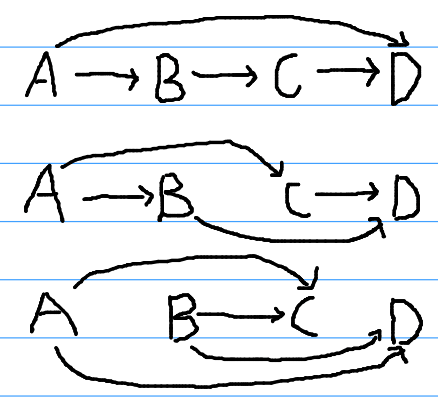
• 这里的箭头 \(\to\) 表示排序后小的，指向排序后大的。

• ABCD，我们选择关键点 A，C。观察环可以被分为 \(A\to ?\to C\)，\(A\to ?\leftarrow C\) 这样两条路径

• ABDC，我们选择关键点 A，D。观察环可以被分为 \(A\to ?\to D\)，\(A\to ?\to D\) 这样两条路径

• ACBD，我们选择关键点 A，B。观察环可以被分为 \(A\to ?\leftarrow B\)，\(A\to?\leftarrow B\) 这样两条路径

• 我们发现一组路径有两个箭头构成，第一个一定是 \(\to\)，第二个要么 \(\to\) 要么 \(\leftarrow\) 都可以。

• 于是我们可以枚举 \(u\)，然后按照新图枚举 \(v\)，再按照原图枚举 \(w\)，最后若有多条从 \(u\) 开始到达同一个 \(w\) 的路径，他们两两都能构成四圆环。然后就可以看懂 wiki 写的代码啦！

• 至于复杂度嘛，和三元环又有什么区别呢？只不过是第二次枚举的不是新图而是原图罢了，可是复杂度是按照原图度数推导的啊，那就对啦 \(O(m\sqrt m)\) 尽情枚举把！