阶梯博弈

前言

• 不得不说忘的真快，去年刚学得啊，才半年不到

阶梯博弈

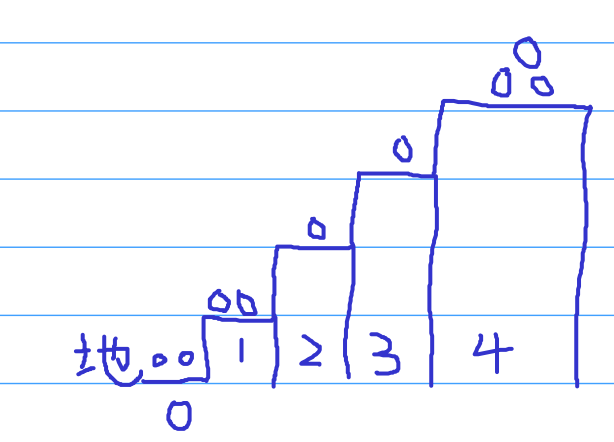
• 就是如图，我们有若干棋子，每一次可以选择若干棋子从一个阶梯挪动到它的下一级阶梯，例如我们可以把 \(3\) 个棋子从 \(4\) 挪到 \(3\)，当所有棋子都在地上就不能再移动了。两个人轮流，谁先挪不动谁输。
• 先说结论，我们把奇数台阶上的棋子作 nim 游戏，就是异或和为 \(0\) 先手输，否则后首输。
• 先考虑只有奇数台阶上有的棋子的情况。我们每次作nim游戏的选择，若一人选择删除一些棋子，相当于把奇数台阶移动到偶数台阶。若一人把偶数台阶移动到奇数台阶，若破坏了另一人的必胜局面，另一人可以把那些棋子继续向下移动，异或和没有变，若是先手此时必胜，就没有必要挪动偶数台阶，大概就这样，基本上就证明完了。

[SDOI2019] 移动金币

• 转化成算两个金币间隔的距离，作阶梯博弈就好了
• 此时我们相当于把序列划分成\(m+1\)数段，那么只需要保证偶数段异或和不为 \(0\) 即可
• 直接作是 \(O(n^2m)\) 的复杂度太高。
• 而我们只需要反着考虑异或和为 \(0\) 的即可，因为异或和为 \(0\) 我们可以考虑二进制拆位，每个位的个数为偶数即可。