LGV 引理（我还没太想明白，不要被我误导了啊

LGV 引理

条件

• 只作用于有向无环图

定义

• \(w(P)\) 表示路径 \(P\) 的所有边权的乘积
• \(e(u,v)=\sum_{P:u\to v}w(P)\) 表示所有从 \(u\to v\) 的路径的 \(w(P)\) 之和
• 起点集合 \(A=\{A_1,A_2,\cdots,A_n\}\)
• 终点集合 \(B=\{B_1,B_2,\cdots,B_n\}\)
• \(P:A\to B\) 中的 \(P\)，是一组 \(n\) 个路径 \(P_1:A_1\to B_{\sigma_1},P_2:A_2\to B_{\sigma_2},\cdots,P_n:A_n\to B_{\sigma_n}\)，
• \(P^u:\) 要求这 \(n\) 条路径点不相交
• \(P^c:\) 要求这 \(n\) 条路径点相交
• 矩阵 \( M = \begin{pmatrix}e(A_1,B_1)&e(A_1,B_2)&\cdots&e(A_1,B_n)\\ e(A_2,B_1)&e(A_2,B_2)&\cdots&e(A_2,B_n)\\ \vdots&\vdots&\ddots&\vdots\\ e(A_n,B_1)&e(A_n,B_2)&\cdots&e(A_n,B_n)\end{pmatrix}\)

\[\begin{aligned} \det(M)&=\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^ne(A_i,B_{\sigma_i})\\ &=\sum_{P^u:A\to B}(-1)^{t(\sigma(P^u))}\prod_{i=1}^nw(P^u_i) \end{aligned} \]

证明

\[\begin{aligned} \det(M)&=\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^ne(A_i,B_{\sigma_i})\\ &=\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^n\sum_{P:A_i\to B_{\sigma_i}}w(P)\\ &=\sum_{P:A\to B}(-1)^{t(\sigma(P))}\prod_{i=1}^nw(P_i)\\ &=\sum_{P^u:A\to B}(-1)^{t(\sigma(P^u))}\prod_{i=1}^nw(P^u_i)+\sum_{P^c:A\to B}(-1)^{t(\sigma(P^c))}\prod_{i=1}^nw(P^c_i) \end{aligned} \]

• 只需证，\(\sum_{P^c:A\to B}(-1)^{t(\sigma(P^c))}\prod_{i=1}^nw(P^c_i)=0\)

• 考虑描述一种 \(P^c\)，可以用 \(n\) 个路径唯一确定，从而 \(n\) 个路径能唯一确定一个，相交集，即，若 \(P^c_i\)，\(P^c_j\) 有交点，则 \(\{i,j\}\in\) 相交集。

• 不妨给相交集钦定一个偏序关系，\(\{a,b\}<\{c,d\}\) 当且仅当，\(min(a,b)< min(c,d)\) 或者 \(min(a,b)=min(c,d)\) 且 \(max(a,b)<max(c,d)\)

• 我们取一个相交路径组里，在偏序集的最小的一对路径，\(P^c_a,P^c_b\)

• 那么我们必然有一个路径组与其对应。那个路径组除了 \(P^c_a,P^c_b\) 其他路径都相同，设 \(P^c_a,P^c_b\) 的一个交点为 \(x\)，则可构造 \(P_a^c\) 变为 \({P^c_a}_1\cdots\to x\to {P^c_b}_{end}\) 同理 \(P_b^c\) 变为 \({P^c_b}_1\cdots\to x\to {P^c_a}_{end}\)

• 而正好发现，一对对应的路径组权值相同，逆序对和为偶数，正好相互抵掉，于是，原式为 \(0\)

应用

[Justice For Everyone QOJ](Justice For Everyone - 题目 - QOJ.ac)

• 假设不考虑任意时刻不能相等的限制，考虑容斥
• 约定 \(d_i=b_i-a_i\)，\(D=\frac{1}{2}\sum d_i\)，\(S=\sum c_i\)

\[\begin{aligned} ans&=\sum_{S}(-1)^{|S|}\binom{|S|}{c_1,c_2,\cdots,c_n}\binom{2(D-|S|)}{d_1-2c_1,d_2-2c_2,\cdots,d_n-2c_n}\\ ans&=\sum_{s=0}^D(-1)^{s}\binom{D}{s}\binom{s}{c_1,c_2,\cdots,c_n}\binom{2(D-s)}{d_1-2c_1,d_2-2c_2,\cdots,d_n-2c_n}\\ ans&=\sum_{s=0}^D(-1)^{s}\binom{D}{s}s!2(D-s)![x^s]\prod_{i=1}^n\sum_{c=0}^{\lfloor\frac{2}{d_i}\rfloor}\frac{x^c}{(d_i-2c)!c!} \end{aligned} \]

• 然后我们考虑有限制，不妨画出坐标系

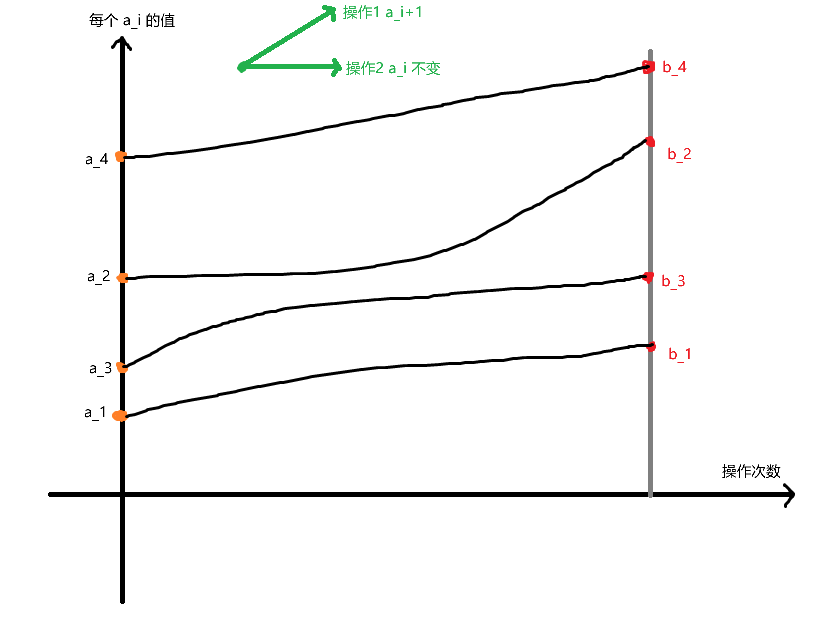
• 对于每个点，我们可以选择操作 1 或者 操作 2 求所有不想交路径的方案数。但有限制，每次此操作，恰好只能有两个 操作 1 作用于不同的 \(a_i\)。
• 网格图不相交路径计数，不由自主想到 LGV引理，还记得这个吗

\[\det (M)=\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^n e(A_i,B_{\sigma_i}) \]

• 这个式子再往后，就等于不相交路径数，嗯，\(e(A_i,B_{\sigma_i})\) 算不出来，因为上面的容斥是合在一起算的，但 \(\prod\limits_{i=1}^n e(A_i,B_{\sigma_i})\) 在原引理中，表示的是所有 \(P:A\to B_\sigma\) 的方案。这个恰为上面求得的容斥。
• 可，真的可以这样做吗？应该是可以的（我也没想的很明白）。若这样可以，只需保证，LGV 中 \((-1)^{t(\sigma)}\) 能把相交路径容掉。从总的方案来算，考虑 LGV 的证明，首选权值不会变，即所有边权的积，哪怕带容斥系数，在 \(s\) 相同的时候也总能找到对应的方案，至于 \(s\) 所钦定的方案，与 LGV 计数的容斥无关。逆序对数，就更为显然，由此我们可以，两个容斥套在一起，LGV 直接算总贡献。

\[\begin{aligned} ans&=\sum_{s=0}^D(-1)^{s}\binom{D}{s}s!2(D-s)![x^s]\prod_{i=1}^n\sum_{c=0}^{\lfloor\frac{d_i}{2}\rfloor}\frac{x^c}{(d_i-2c)!c!}\\ ans&=\sum_{\sigma}(-1)^{t(\sigma)}\sum_{s=0}^D(-1)^{s}\binom{D}{s}s!2(D-s)![x^s]\prod_{i=1}^n\sum_{c=0}^{\lfloor\frac{b_{\sigma_i}-a_i}{2}\rfloor}\frac{x^c}{(b_{\sigma_i}-a_i-2c)!c!}\\ ans&=\sum_{s=0}^D(-1)^{s}\binom{D}{s}s!2(D-s)![x^s]\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^n\sum_{c=0}^{\lfloor\frac{b_{\sigma_i}-a_i}{2}\rfloor}\frac{x^c}{(b_{\sigma_i}-a_i-2c)!c!}\\ F_d(x)&=\sum_{c=0}^{\lfloor\frac{d}{2}\rfloor}\frac{x^c}{(d-2c)!c!}\\ \det(M)&=\sum_{\sigma}(-1)^{t(\sigma)}\prod_{i=1}^n F_{b_{\sigma_i}-a_i}(x) \end{aligned} \]