函数的凸性

写在前面的

• 注：本文大部分内容在是对 2023年集训队论文集中《浅谈函数的凸性在 OI 中的应用——郭羽冲》的转述，心得，学习笔记。
• 注：本文兴趣化严重，只深入研究作者的一些感悟，忽略了很多作者自认为会的东西，并不很适合作为初学文章。

斜率优化

• 所谓斜率优化，是对 \(dp\) 转移的一种优化。顾名思义有时，\(dp\) 的状态数可能不是很多，但是 \(dp\) 每个状态的求解，确可能需要从 \(O(n)\) 状态转移过来，所以总复杂度就高了。

• 举例：将序列 \(a\) 划分成若干子段，代价为 段数\(\times w+\)每一段的 \(a_i\) 和的平方，要求最小化代价

• 设前缀和 \(s_i\)，有转移 \(dp_i=\min\limits_{j=0}^{i-1}\{dp_j+(s_i-s_j)^2+w\}\)

• 观察，\(dp_{0,1,\cdots ,i-1}\to dp_i\) 都会有转移

• 对于每一个转移，列出他的 \(dp\) 式，\(dp_i=dp_j+(s_i-s_j)^2+w=dp_j+s_i^2+s_j^2-2s_is_j+w\)

• 我们将原问题放在直线与点上考虑，即考虑直线 \(y=kx+b\)，其中 \((x,y)\) 为一组，\((k,b)\) 为一组

• 我们有两种思路

  • 若把已知的 \(dp\) 值看做 \((x,y)\)，那么在算未知的 \(i\) ，就是要求固定斜率的直线与 \(y\) 轴交点的纵坐标
  • 具体的，\(dp_j+s_j^2=2s_is_j+dp_i-s_i^2\)，\((s_j,dp_j+s_j^2)\) 视作一个点，那么过 \((s_j,dp_j+s_j^2)\) 的斜率为 \(2s_i\) 的直线，于 \(y\) 轴的交点即为 \(dp_i-s_i^2\)，由此我们借助上下凸克来快所有可转移的直线中，交点中坐标最小的直线，就是通过加 \(s_i\) 解出 \(dp_i\)
  • 若吧已知的 \(dp\) 值看做 \((k,b)\)，那么在算未知的 \(i\) 就是，选出固定的 \(x\) 横坐标，和若干组直线的交点。
  • 具体的，\(dp_i-s_i^2=-2s_js_i+dp_j+s_j^2\)，\((k,b)=(-2s_j,dp_j+s_j^2)\) 视作以条直线，那么在直线 \((k,b)=(-2s_j,dp_j+s_j^2)\) 上的所有横坐标为 \(s_i\) 所对应的纵坐标即为 \(dp_i-s_i^2\)，由此我们只需要用李超树即可优化转移过程。

四边形不等式

• 若矩阵 \(A_{i,j}\) 满足四边形不等式，当且仅当，\(\forall a<b\le c<d,A_{a,c}+A_{b,d}\le A_{a,d}+A_{b,c}\)。这等价于 \(\forall a<b,A_{a,b}+A_{a+1,b+1}\le A_{a,b+1}+A_{a+1,b}\)
• 我们假象一种 \(dp_i=\min\{dp_j+calc(i,j)\}\)，令 \(calc(i,j)=A_{i,j}\)
• 我们重写 \(\forall a<b\le c<d,calc(a,c)+calc(b,d)\le calc(a,d)+calc(c,b)\)
• 值得注意的：没准这里的 \(\le\) 可以当做偏序关系来理解，不是不可以 \(\ge\) ，\(min,max\)，上下凸壳依旧相辅相成。

满足决策单调性

• 设 \(dp_x\) 的最优决策点为 \(a\)，\(dp_y\) 的最优决策点为 \(b\)，即 \(dp_a\to dp_x,dp_b\to dp_y\)

• 若 \(dp_i=\min\{dp_j+calc(i,j)\}\) 中的 \(calc(l,r)\) 满足四边形不等式，那么有最优决策点 \(x<y,a\le b\)

• 若是自己探索决策单调性应满足的限制的话

  • 不是吧，其实我想不下去了，因为之前想的都是错的，我应该是没有任何头绪的，哪怕是一点点关于单调性的约束。
  • 困难在哪呢，困难在若是想要完美的限制决策单调性，我们可能需要枚举所有的转移点，若是这样想大概率也是一个时间复杂度大小的限制，不太具有推广性。

• 神奇的，就在于四边形不等式用了一种弱的，对对立问题的限制，较强的约束了原问题。

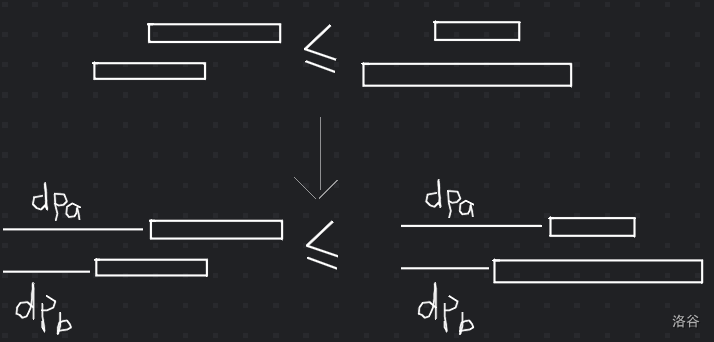
• 如图所示，我们说，若反面 \(x<y,a>b\) 的决策点更优，则反面总和一定更优，而我们发现限制反面决策不优是困难的，因为正如上文我们需要枚举决策点。而要是只限制反面总和不优，一定是更强的限制，且可以做到。若反面总和更优应满足 \(dp_a+dp_b+[a,d]+[b,c]<dp_a+dp_b+[a,c]+[b,d]\)。
• 若构造 \([a,d]+[b,c]\ge [a,c]+[b,d]\) 那反面总和就没有机会更优，所以所有的反面一定不优，那决策单调性就一定单调。
• 咦，我们总和，比之枚举的好处在呢？决策点，单调。想要证明，涉及 \(dp\) 状态 \(dp_i\)，最优决策点 \(b\)，反正决策点 \(a\)。若 \(i\) 恒定，还有两个变量，若在钦定一个还剩一个。那是不是用二元关系的函数，来限制会更简单，一元关系需要枚举，这么说的话，是不是钦定两个决策点 \(a,b\) 用状态和作为函数比较，得到了一个比较强的约束。
• 哎，我在说什么，或许在证实一种猜想，或许在自圆其说，总是，给我不会的东西找理由。

满足关于段数那维成凸性

• 这个，请自行看论文，超出能力范围，并没有独到的感悟

寻找凸性的三种方法

• 转移满足四边形不等式矩阵，最小值，最大值，关于段数，成下凸、上凸关系。

• 可构造费用流模型，可以证明最小费用、最大费用，关于最大流流量的不同、承下凸，上凸关系。

• 亦可以考虑凸函数的直接相加。在不就定义了吧

wqs 二分

• 若我们要，求的东西是凸的，而且只关心凸函数的一个点的值，我们可以通过二分斜率，每次得到当前斜率的直线与凸壳边界相交的位置，找到那个位置的横坐标，即段数，和我们所需的段数的差距，之后继续进行二分调整。

• 我们二分有什么好处呢？好处在于把一个限制划分区间个数的 \(dp\) 化为，任意划分的 \(dp\) 这种 \(dp\) 往往可以少一维状态，有时还可以进一步优化。

• 值得注意的是，我们怎么求当前斜率与凸包且的点的最小代价在哪呢？

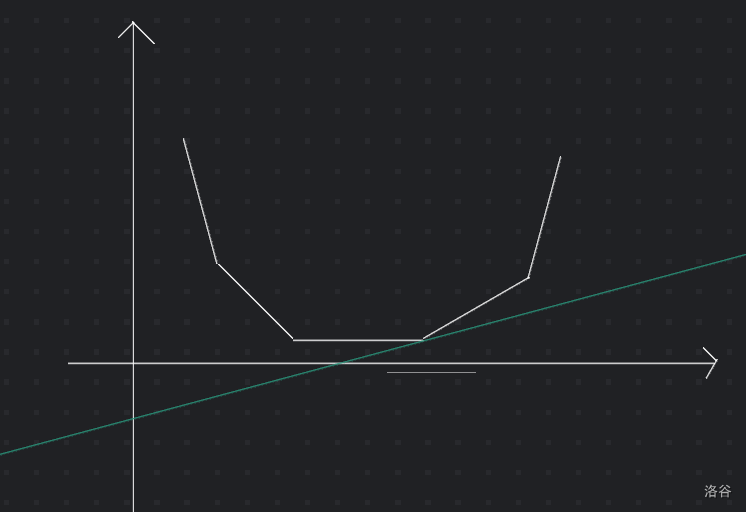
• 这是我们想要的最低点。他与别的情况有什么不同呢

• 显然，它是与 \(y\) 轴交点最小的点

• 那我们在设计 \(dp\) 的时候不妨将每一段的贡献，减去 \(k\) 我们二分的斜率，这样的话总答案就是，真实答案\(-\)段数\(\times k\)，这恰好是与 \(y\) 轴相交纵坐标的值，我们只要算出它的最小值的的段数，就是取到最低点的段数。这样我们就巧妙的通过减一个贡献的方法，扩展到了取任意段的做法。
• 其实我知道我没讲清楚，只不过是我的一些感受罢了，怎么说以后有时间再来完善吧。

\((min,+)\)，\((max,+)\) 卷积

• \(f_i=\min\limits_{x=0}^i\{a_{x}+b_{i-x}\}\) 这就是所谓的 \((min,+)\) 卷积

• \(f_i=\max\limits_{x=0}^i\{a_{x}+b_{i-x}\}\) 这就是所谓的 \((max,+)\) 卷积

• 对于大多是情况，这种卷积是没有办法快速进行的，给出序列 \(a,b\) 需要 \(O(\text n^2)\) 才能计算出答案

• 有特例，若 \(a,b\) 都是下凸函数，则可以通过按斜率排序 \(O(\text n)\) 快速生成 \((min,+)\) 卷积的 \(f\)。

• 若 \(a,b\) 都是上凸函数，则可以通过按斜率排序 \(O(\text n)\) 快速生成 \((max,+)\) 卷积的 \(f\)。

维护凸函数 slope trick

• 其实就是用堆呀，set 什么的维护，斜率变化的位置。
• 以下凸为例，斜率必然单调上升，我们维护在店 \(x\) 斜率上升了多少，即可，不维护斜率不变的位置。
• 有时可能需要记录 \(x=0\) 的 \(f(x)\) 值，这样的话就能把整个函数求出来，有时候分段维护，一部分斜率小于 \(0\) 一部分斜率 \(\ge 0\)，动态记录斜率为 \(0\) 的位置就是最小值。