理论力学笔记

目录

第一章 静力学公理和物体受力分析

1-3 物体的受力分析和受力图

分析构件受几个力，这些力的方向、作用位置，就是受力分析。

力可分为主动力和从动力。主动力一般已知，从动力大多是约束对被约束体的约束力。

受力分析的步骤

  1. 取研究对象
    1. 优先选主动力已知最多的构件，或者未知力最少的构件
    2. 注意二力杠[1]
  2. 分析主动力
  3. 分析从动力：注意约束类型对应的力系

细节

  1. 二力杠无论形状，受力总沿着两端点连线，等值反向

  2. 不能多画也不能少力，并且约束力要严格按照约束性质作图

  3. 假定了作用力的方向，则反作用力的方向一定与之相反，不能改变

  4. 内力外力对不同研究对象来说是不同的。如果对研究对象而言是内力，则不画出简图。

  5. 当滑轮和多个杠构成复合铰链时，通常认为复合铰链在滑轮上，这时每个杠对复合铰链的作用合力等于滑轮受到的力

    如果是多个杠构成复合铰链，则可以选定复合铰链在某个杠上，或者直接把它分离出来

1-4 力学模型与力学简图

力学模型：简化的力学问题

力学简图：用简单图形表示的力学模型

从实际问题抽象到力学模型和力学简图是十分复杂且重要的一环，需要其他学科知识的支撑。

抓住问题的本质与关键，忽略次要的东西。

简支梁

无论是过河的独木桥，还是平房上的木梁，只要是直接放，就可以看成一端固定支架，另一端滚动支架的模型

第二章 平面力系

2-1 平面汇交力系

所有力作用线汇交于一点的力系叫做平面汇交力系。

平面汇交力系可用几何法或解析法来求合力：

  1. 几何法：核心——力的三角形法则
    1. 将力两两合成，最后形成力多边形。力多边形若封闭，则合力为；反之沿着未封闭的线，从起点到终点的矢量，就是力系的合力
    2. 平衡条件：力多边形封闭
  2. 解析法：核心——分解、投影
    1. 将每个力分解为x轴方向和y轴方向的正交力。x轴分力的大小叫做力在x轴上的投影，同理有力在y轴上的投影[2]。
    2. x轴上投影的加和为合力在x轴上的投影，即：\(\sum^n_{i=1}F_{i_x}=F^R\) ；y轴上投影的加和等于合力在y轴上的投影,同时合力 \(F=\sqrt{F_x^2+F_y^2},\tan \alpha=\frac{F_y}{F_x}\)

2-2 平面力偶系

平面力对点之矩

  • 定义：平面力对点之矩即通常提到的力矩，是力绕着特定点旋转形成的力矩。

  • 计算公式：\(\vec{M}=\vec{x}\times\vec{F}\),其中\(\vec{x}\)是力相对于转轴点的位矢。

    • 只计算大小，则有：\(M=Fd=Fx\sin \theta\)，其中\(\theta\)是x与F所成夹角，\(d\)是力臂，是力的作用线到转轴点的垂直（最近）距离。

    • 当力的作用线通过转轴时，则\(M=0\)

  • 合力矩定理：平面汇交力系的合力对平面任意一点的力矩等于所有分力各自对这一点的力矩的代数和，即\(M_0(F_R)=\sum M_0(F_i)\)

    • 按照此定理可以快速计算力对某一点的力矩（拆分成沿着两点沿线和垂直两点沿线的方向）

均布力的计算

正方形均布力：对于分布在长为\(l\)，处处力的大小为\(q\)的均布力，其合力为\(ql\),且作用在\(\frac{l}{2}\)处。

三角形均布力：对于分布在长为\(l\),处处力的大小满足\(F(x)=kx\)的均布力，其合力为\(\frac{1}{2}ql\),且作用在离\(x=0\)的\(\frac{2}{3}ql\)处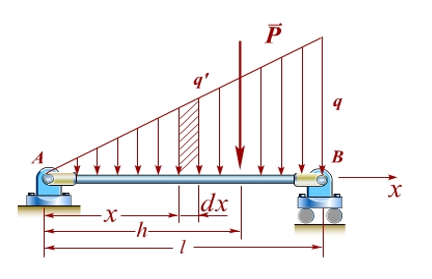image-20201012224117147

梯形均布力：通常是直角梯形，位置则距离力较小的部分有\(\frac{2}{3}l(1-\frac{1}{2}\frac{q_1}{1_1+q_2})\)，合力的大小为\(\frac{1}{2}(q_2-q_1)l+q_1l\)。公式较为复杂，建议将之分割为三角形和矩形两个力，分别按照对应公式计算即可。

平面力偶系

  • 力偶：一对平行相等反向且不共线的力。
    • 力偶无法被合成为一个力，是除了单个力之外的作用最小作用单位。
    • 作用效果：让物体旋转，因此有矩
    • 力偶的作用面：力偶所在平面
  • 平面力偶矩：衡量力偶对物体作用效果（旋转）的物理量
    • \(M=Fd\),其中\(F\)为力的大小，\(d\)为力偶两个力的距离。
    • 主要性质：
      1. 力偶矩没有矩心，对刚体任意一点力偶矩不变；但是力对点之矩会有差别
      2. 力偶矩不变时，力偶在作用面内任意移动旋转，并且力的大小和力偶距离变化，均不影响力偶的作用效果
  • 平面力偶的合成：平面合力偶矩=所有分力偶矩的代数和
  • 合力偶矩为0，则平面力偶系平衡

2-3 平面任意力系的简化

  • 平面力平移定理：力可以平移至任意位置，只是需要加上一个对应的力偶

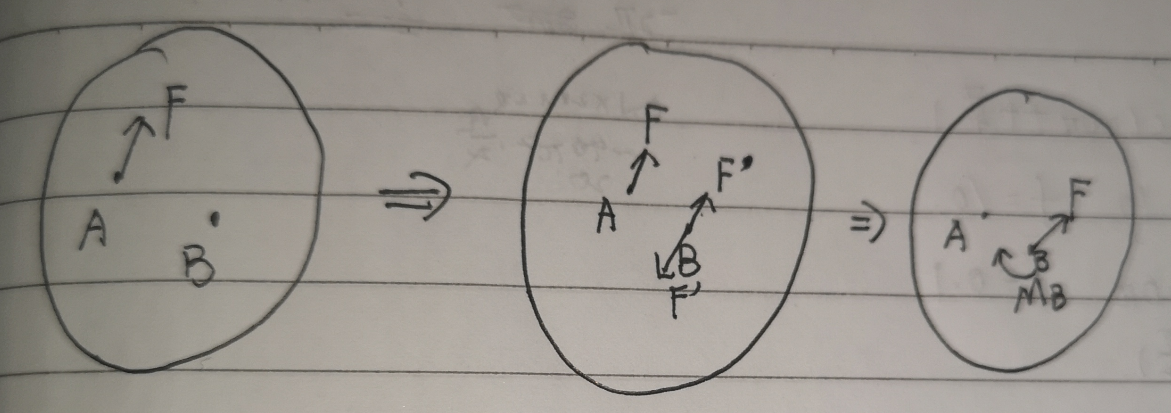
    • image-20201013193929184
    • 原理：加减平衡力系，总力系的作用效果不变，因此在B点加减一对与F相等的平衡力，则F'与F构成力偶，F力平移到B点

  • 简化：

    • 结果取决于合力与合力偶矩是否为0

    • 合力 合力偶矩 结果
      0 0 平衡
      不为0 0 受合力作用
      0 不为0 受合力矩作用
      不为0 不为0 受到合力+合力偶作用，根据平面力平移定理，转化为一个力

  • 约束补充：固定端约束

    • 物体一端完全嵌入另一物体（always walls or ground），可简单看作存在一个力和一个力偶的约束，通常力分解为正交的两个分力，即3个未知量。

2-4 平面任意力系的平衡条件和平衡方程

根据2-3中提到的，平面任意力系的平衡条件是主力和主力矩均为0.将主力分解为沿x、y轴方向的两个分力，有：

\[\sum F_x=0 \\ \sum F_y=0\\ \sum M_o=0 \]

此称为基本式，最常用。

另外两组平衡方程：

  • 两矩式：\(\sum M_A=0 \\ \sum M_B=0 \\ \sum F_x=0\)，其中AB连线不垂直于x轴（可换为y轴）
  • 三矩式：\(\sum M_A=0 \\ \sum M_B=0 \\ \sum M_C=0\)，其中ABC三点不共线

拓展

当平面内只有一个未知力在x方向，其他力都在y方向时，若刚体平衡，显然x方向上的未知力为0。

因此y轴合力为0、合力矩为0构成两个方程。

2-5 物体的平衡、静定与超静定问题

静定与超静定

工程中讨论的力学对象大多是由多个物体组成的系统。根据2-4中所提到，通常系统中一个物体能够求解出3个未知量。

因此有：

  • 静定问题：可求出的未知量数目=未知量数目
  • 超静定问题：可求出的未知量数目＜未知量数目

超静定问题不属于刚体范畴，不予考虑。

求解物体平衡问题

  • 首先对整体分析
  • 无法解决问题则拆解整体，隔离研究对象
    • 优先选择未知量小于等于3的研究对象（一般不取二力杠）
    • 不求解圆柱销顶约束力，则将滑轮与物体看作整体
    • 可以将矩心取为较多未知力的交点
    • 投影轴尽量与较多未知力垂直（通常正交，物体斜放时需考虑）
  • 求解出需要的数据
  • 顺次再取研究对象求解数据，直到解决问题；注意取一次研究对象就解决一部分未知数，尽量不联立多个研究对象的方程组

2-6 平面简单桁架

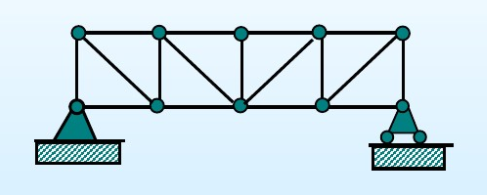
  • 桁架：两端靠铰链连接的一系列杆件，几何形状不变
  • 简单桁架：从三角形开始搭建二元体形成
    • image-20201013202210198
  • 理想桁架：
    1. 各轴线共面且均为2力杠
    2. 杠之间用光滑铰链连接
    3. 杠无自重（一般不考虑）
    4. 力均作用在节点上，且位于桁架几何平面
  • 零杠：
    • 两杠相交，无载荷，两杠均为零杠
    • 三杠相交，其中两杠共线，另外一杠为0杠1
    • 两杠相交，受与其中一杠共线的力，则另外一杠为零杠
  • 计算杆件内力方法：
    1. 节点法
      1. 适用于需要求出所有杆件力的情况
      2. 整体--所有节点依次分析，相当于分析多个平面汇交力系的平衡问题
    2. 截面法
      1. 适用于求出部分杆件受力情况
      2. 取一平面将需要求出的杆件截断，根据情况分析剩下的部分
      3. 截断后的部分作为一整个刚体，杠与杠之间的作用力不需要考虑，只考虑杠作用于节点的力和已知力
      4. 相当于分析一个平面任意力系的平衡问题

注释

  1. 只受二力而平衡的构件叫做二力构件，对刚体而言无论形状都称为二力杠。二力杠受的两个力总沿着两端点连线，且等值反向 ↩︎

  2. 投影是具有正负的标量，根据提前设定的方向来确定正负。假设沿着x轴正方向的投影为正，反之则为负 ↩︎

posted @ 2020-10-10 16:24  夜尘Dakeniz  阅读(2795)  评论(0)    收藏  举报